Вопрос 2. Принципы формирования канальных сигналов

В системах передачи с ВРК переносчиками являются периодиче­ские последовательности прямоугольных импульсов (ПППИ), сдвинутые относительно друг друга на величину защитного интервала τ_з (см. рис.2), параметры которых изменяются по законам изменения первичных сигналов.

Периодическая последовательность прямоугольных импульсов с указанием всех ее параметров приведена на рис.3.

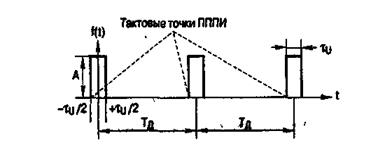
Рис.3. Переносчик - периодическая последовательность прямоугольных импульсов

Основными параметрами ПППИ являются: А - амплитуда им­пульсов, τ_и - длительность (ширина) импульсов Т_д - период следо­вания импульсов или F_д= 1/Т_д - частот следования или тактовая частота периодической последовательности импульсов (круговая частота следования Ω_д = 2πF_д),положение импульсов относительно тактовых точек 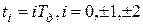и отношение T_д/τ_и,называемое скважностью ПППИ. В современных СП с ВРК величи­на скважности лежит в пределах 20...2500.

Периодическую последовательность прямоугольных импульсов можно представить в аналитической форме

f(t)= 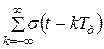, (1)

где σ(t) - функция описывающая одиночный импульса исходной последовательности f(t).

Для ПППИ (см. рис. 3) функция σ(t) имеет вид:

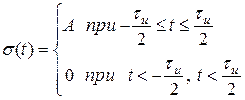. (2)

С другой стороны, ПППИ f(t) может быть представлена рядом Фурье:

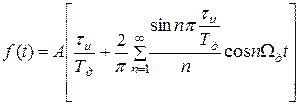, (3)

где, напомним, Ω_д = 2π/ Т_д - круговая частота последовательности f(t).

Как следует из (3), спектр ПППИ включает в себя постоянную со­ставляющую с амплитудой, равной

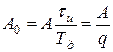
и гармоники частоты следования-частоты дискретизации с ампли­тудами:

.

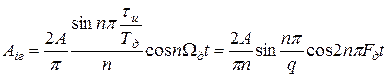Спектр ПППИ представлен на рис.4.

Рис. 4. Спектр амплитуд периодической последовательности прямоугольных импульсов

Известно, что огибающая спектра амплитуд ПППИ соответствует спектру одиночного прямоугольного импульса длительностью τ_и,а число гармоник тактовой частоты (частоты следования) до первого нуля спектра амплитуд равно q - 1, т.е. на единицу меньше скваж­ности последовательности импульсов q. И еще, более 90...95 % мощности периодической последовательности импульсов сосредо­точено в полосе частот от 0 до F_max = 1/τ_и.Следовательно, для передачи исходной ПППИ по каналам, трактам и линиям связи их полоса частот должна быть не менее ΔF = 1/τ_и.

Формирование канальных сигналов в СП с ВРК осуществляется на основе модуляции одного из основных параметров ПППИ. В основном нашли применение три вида импульсной модуляции: амплитудно-импульсная (АИМ), широтно-импульсная (ШИМ) и временная импульсная модуляция (ВИМ), разновидностями которой являются фазоимпульсная модуляция (ФИМ) и частотно-импульсная модуляция (ЧИМ).

Формирование канальных сигналов с помощью амплитуд­но-импульсной модуляции. При амплитудно-импульсной модуля­ции амплитуда ПППИ изменяется по закону первичного или моду­лирующего сигнала c(t), а длительность импульсов, частота их следования и положение относительно тактовых точек при АИМ остаются постоянными. На рис. 5 показаны временные диаграммы формирования АИМ канального сигнала.

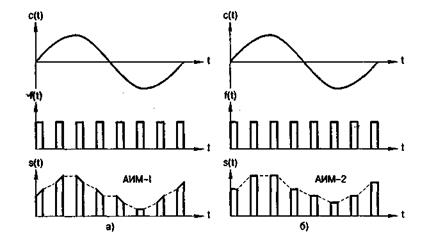
Рис. 5. К пояснению принципов амплитудно-импульсной модуляции

На рис.5 показано, что первичный сигнал c(t) модулирует ампли­туду ПППИ f(t) в результате получается канальный амплитудно-модулированный сигнал s(t). При этом различают два вида ампли­тудно-импульсной модуляции (АИМ):

амплитудно-импульсная модуляция первого рода (АИМ-1), при которой мгновенное значение амплитуды импульсов зависит от мгновенного значения модулирующего сигнала, вершины импульсов повторяют исходный сигнал на длительности импульсов (рис. 5, а);

амплитудно-импульсная модуляция второго рода (АИМ-2), при которой амплитуда импульсов остается постоянной на всей его длительности (рис. 5, б). При скважности ПППИ q > 10 различия между АИМ-1 и АИМ-2 практически исчезают и потому в даль­нейшем не будем делать различия между этими видами ампли­тудно-импульсной модуляции.

Для оценки полосы частот, необходимой для передачи АИМ ка­нальных сигналов, возможностей их демодуляции и сравнения различных видов импульсной модуляции определим спектр АИМ сигнала при модуляции синусоидальным сигналом

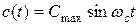(4)

и при модуляции сложным сигналом с ограниченным спектром частот.

В самом общем случае амплитудно-модулированный (каналь­ный) сигнал s(t) можно описать следующим аналитическим выраже­нием

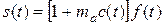, (5)

здесь т_а - коэффициент, характеризующий глубину модуляции; c(t) - модулирующий (первичный) сигнал; f(t) - периодическая последо­вательность импульсов. Подставив в (5) выражения для c(t) (4) и f(t) (3), получим выражение для АИМ канального сигнала:

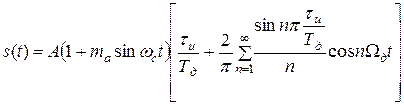, (6)

здесь .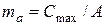

Сделав в (6) замену вида q=τ_и/T_д и выполнив несложные триго­нометрические преобразования, получим

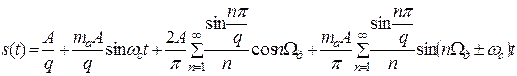(7)

Из формулы (7) следует, что АИМ канальный сигнал содержит постоянную составляющую с амплитудой

A₀ = A/q, (8)

исходный модулирующий сигнал:

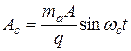, (9)

гармоники частоты следования ПППИ - частоты дискретизации,

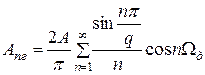(10)

и боковые частоты около гармоник частоты дискретизации

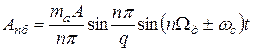. (11)

Если модулирующий сигнал является многочастотным, зани­мающим полосу частот от ω₁ до ω₂, то спектр АИМ канального s(t) сигнала будет содержать постоянную составляющую, исходный сигнал занимающий полосу частот от ω₁ до ω₂,гармоники частоты дискретизации пΩ_д и нижние и верхние боковые полосы частот вокруг гармоник частоты дискретизации, занимающие полосы частот пΩ_д±(ω₁…ω₂).

Амплитуды составляющих многочастотного АИМ канального сиг­нала определяются из формул (8-11). Спектр АИМ сигнала S(f) при модуляции сигналом со спектром С(f),ограниченным круговыми частотам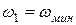и и 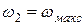или нижней граничнойчастотой F_МИН и верхней граничной частотой F_МАKC,показан на рис.6.

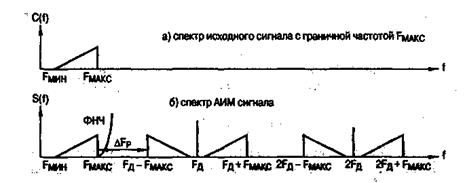
Рис. 6. Спектр АИМ сигнала при модуляции ПППИ сигналом с ограниченным спектром

Как следует из рис.6, б в спектре АИМ сигнала содержится и ис­ходный сигнал. Следовательно, процесс демодуляции АИМ сигнала можно осуществить фильтром нижних частот (ФНЧ). Но для неискаженного выделения первичного сигнала полоса расфильтровки ФНЧ ΔF_P между полосой частот исходного сигнала с верхней граничной частотой F_маx и нижней боковой полосой частот около первой гармони­ки частоты дискретизации F_д с нижней граничной частотой F_д – F_мах равна

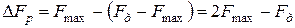. (12)

Из последнего выражения следует, что при использовании «иде­ального фильтра нижних частот», полоса расфильтровки ΔF_P = 0 и, следовательно, выполняется равенство F_д = 2F_max, соответствую­щее теореме Котельникова. Но изготовить фильтры можно только с конечной крутизной характеристики затухания в переходной об­ласти и потому для обеспечения неискаженного восстановления первичного сигнала из АИМ сигнала должно выполняться условие:

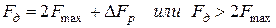. (13)

Для каналов тональной частоты максимальная частота F_мах = 3,4 кГц и частоту дискретизации принимают равной F_д = 8 кГц, т.е. больше 6,8 кГц. Период дискретизации при этом равен Т_д = 1/F_д = 1/8000 = 125 мкс. При этом полечи расфильтровки ФНЧ, осуществляющего демодуляцию АИМ канального сигнала, равна ΔF_P = 1,2 кГц.

Длительность канальных импульсов τ_и в СП с ВРК на основе АИМ зависит от числа каналов N и от скважности импульсов группового сигнала γ,которая определяется (см. рис.2) соотношением вида

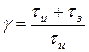,(14)

где τ₃ - длительность защитного интервала между импульсами соседних каналов. Длительность импульсов в N - канальной систе­ме передачи с АИМ может быть определена из выражения

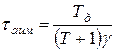, (15)

где Т_д = 1/F_д - период дискретизации; (N +1) - общее число ка­нальных импульсов (с учетом синхросигнала - СС) за период Т_д. При 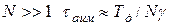.Обычно скважность группового сигнала γ = 2. Полоса частот необходимая для передачи АИМ группового сигнала принимается равной:

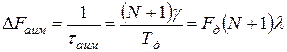. (16)

Системы передачи с ВРК на основе амплитудно-импульсной мо­дуляции отличаются простотой построения оконечных станций, однако (как будет показано ниже) обладают низкой помехоустойчи­востью и весьма критичны к частотным характеристикам линейных, групповых трактов и линий связи. Поэтому в применяющихся на практике СП с ВРК методы АИМ используются на первой ступени формирования канальных сигналов систем передачи с ВРК, исполь­зующих другие виды импульсной модуляции.

Формирование канальных сигналов с помощью широтно-импульсной модуляции. При широтно-импульсной модуляции (ШИМ) длительность импульсов ПППИ изменяется под воздействи­ем модулирующего первичного сигнала, а остальные параметры ПППИ остаются неизменными. Различают одностороннюю (рис.7) и двустороннюю ШИМ.

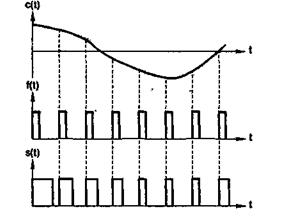
Рис. 7. К определению односторонней широтно-импульсной модуляции

На практике наибольшее применение находит односторонняя ШИМ (ОШИМ). При ОШИМ изменение длительности импульса ПППИ происходит только за счет перемещения одного из фронтов (например, заднего), а положение другого (переднего) фронта остается неизменным относительно тактовых точек ПППИ. При двусторонней ШИМ перемещаются и передний и задний фронты импульсов симметрично относительно их центра, соответствующего тактовым точкам ПППИ.

В зависимости от того, каким образом устанавливается связь ме­жду моментом отсчета мгновенных значений модулирующего сигнала c(t) и шириной импульса ПППИ, различают широтно-импульсную модуляцию первого рода (ШИМ-1) и второго рода (ШИМ-2).

При ШИМ-1 длительность импульсов определяется функцией c(t) в моменты возникновения переднего или заднего фронта импульсов s(t); при ШИМ-2 длительность импульсов s(t) пропорциональна мгно­венным значениям сигнала c(t) в тактовых точках (см. рис.7). При τ_и « Т_д различия между ШИМ-1 и ШИМ-2 несущественны.

Изменения длительности импульсов f(t), вызываемые модули­рующим сигналом c(t), можно описать следующим выражением:

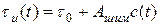, (17)

здесь A_шим - крутизна характеристики широтно-импульсного модуля­тора, мкс/В; τ_о - среднее значение длительности импульсов ШИМ сигнала s(t). Если в (17) подставить c(t) из (4), то получим:

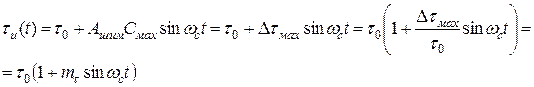(18)

где Δτ_мах - максимальное отклонение фронта импульсов в одну сторону; m_τ - коэффициент широтной модуляции импульсов.

Для определения спектра ШИМ сигнала подставим выражение для τ_u(t) из (18) в формулу для f(t) (3) и, выполнив некоторые преоб­разования, получим

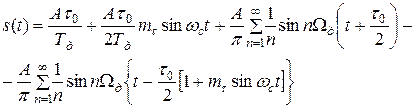(19)

Как следует из последнего выражения, спектр сигнала односто­ронней ШИМ при τ_и«Т_д в своем составе содержит:

постоянную составляющую с амплитудой:

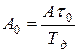(20)

исходный (модулирующий) сигнал:

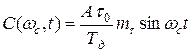; (21)

гармоники частоты дискретизации с амплитудами:

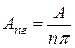; (22)

бесконечное число составляющих вида:

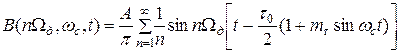(23)

Последнее соотношение можно упростить, если воспользоваться формулой:

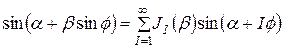, (24)

вытекающей из теории функций Бесселя.

Подставив вышеприведенные соотношения и замены в (23) и выполнив некоторые преобразования, получим:

. (25)

Последнее выражение показывает, что в спектре ШИМ сигнала вокруг гармоник частоты дискретизации содержится бесконечное число верхних и нижних боковых вида ( ).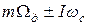

Если модулирующий сигнал c(t) занимает полосу частот ω_мин…ω_мах,то в спектре ШИМ сигнала S (ω) будут содержатся: постоянная составляющая, спектр исходного сигнала, гармоники частоты дискретизации и боковые полосы частот (рис.8).

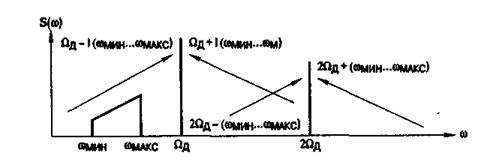
Рис. 8. Спектр ШИМ сигнала

Амплитуды боковых полос частот в спектре ШИМ сигнала, груп­пируются вблизи соответствующих гармоник частоты дискретиза­ции, изменяются в соответствии со значением функций Бесселя J_I (β), которые в свою очередь зависят от аргумента и от номера I, характеризующего порядок функции Бесселя. Это группирование более заметно в области небольших значений п гармоник частоты дискретизации.

При больших n группирование становится менее заметным. По­следнее объясняется тем, что аргумент функции Бесселя β на этих частотах велик, и поэтому спектр боковых полос частот около этих гармоник расширяется.

С ростом величины максимального отклонения (девиации) фрон­та импульса Δτ_мах увеличивается аргумент β функции Бесселя, поэтому он всегда сопровождается ростом интенсивности боковых полос различного порядка вокруг гармоник частоты дискретизации и, следовательно, увеличения комбинационных искажений.

Поскольку при любом значении n и I функция Бесселя существу­ет, ширина спектра боковых полос около каждой гармоники частоты дискретизации теоретически бесконечна, т.е. спектры боковых полос вокруг гармоник неразделимы. Но, что самое неприятное, нижние боковые полосы частот при различных значения n и I вида

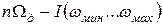(26)

попадают в полосу частот исходного сигнала, что вызывает появле­ние искажений при демодуляции с помощью фильтра нижних частот. Однако при рациональном выборе параметров модуляции эти искажения можно сделать достаточно малыми.

При определении необходимой полосы частот группового тракта для передачи ШИМ сигналов полезно знать следующее:

коэффициент широтной модуляции импульса m_τ= Δτ_мах/τ₀ всегда меньше 1, так как минимальная длительность импульса должна удовлетворять требованию:

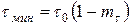. (27)

Обычно m_τ = 0,5...0,75, поэтому

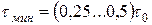. (28)

Если минимальная длительность канального импульса равна τ₀, то ширина полосы частот тракта передачи группового ШИМ сигнала должна быть не меньше

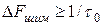. (29)

Из (21) следует, что полезный результат на выходе демодуля­тора зависит не только от величины т_τ,но и от амплитуды им­пульсов, поступающих на демодулятор. Если амплитуда демодулируемых импульсов, например, в результате действия помех изменяется, то полезная компонента первичного сигнала на выхо­де демодулятора оказывается искаженной. Поэтому для устране­ния вредного действия помех применяется ограничение импуль­сов по минимуму и максимуму. В этом заключается преимущество ШИМ перед АИМ.

Широтная импульсная модуляция используется в многоканальных системах передачи импульсной радиосвязи, а также в некото­рых радиотелеметрических системах и системах телеуправления, телеконтроля и телемеханики.

Формирование канальных сигналов на основе фазоимпульсной модуляции. При фазоимпульсной модуляции (ФИМ) сдвиг импульсов ПППИ относительно тактовых точек изменяется по закону первичного (модулирующего) сигнала c(t). Существует не­сколько разновидностей ФИМ, в частности фазоимпульсная моду­ляция первого рода (ФИМ-1), при которой временной сдвиг импуль­сов ПППИ пропорционален значению модулирующего сигнала в момент появления импульса ПППИ, и фазоимпульсная модуляция второго рода (ФИМ-2), при которой временной сдвиг импульсов ПППИ пропорционален значениям модулирующего напряжения в тактовых точках. Обычно применяется ФИМ-2(рис. 9). При отри­цательных значениях модулирующего сигнала импульсы ПППЙ смещаются влево, при положительных - вправо.

Для определения спектрального состава ФИМ сигнала предпо­ложим, что модулирующий сигнал описывается выражением (4). При этом величина временного сдвига k-гoимпульса относительно тактовой точки определяется формулой 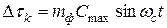,где т_ф -коэффициент глубины модуляции. Обозначим максимальный вре­менной сдвиг 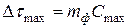. Текущая фаза модулированной по фазе ПППИ определяется величиной Δτ итактовой частотой

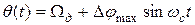, (30)

где 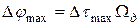- индекс модуляции. Мгновенная частота сле­дования импульсов будет равна:

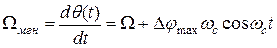. (31)

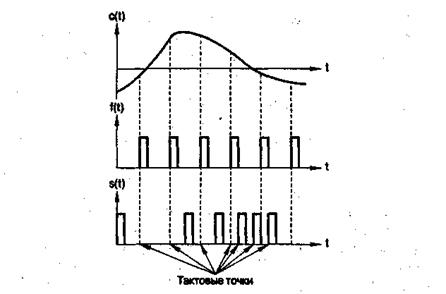
Рис. 9. К формированию канальных сигналов на основе фазоимпульсной модуляций

При подстановке в формулу (3) вместо Ω_дt значения θ(t) из (30) и вместо Т_д - величины Т_мгн= 2π/Ω_мгн,получим выражение для канального ФИМ сигнала:

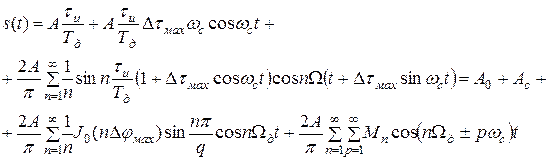(32)

где q – скважность ПППИ, 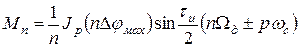, 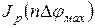- значение функций Бесселя p-го порядка от аргумента nΔφ_мах.

Как следует из формулы (32), спектральный состав канального ФИМ сигнала s(t) включает в себя:

постоянную составляющую с амплитудой

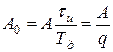(33)

исходный (модулирующий) сигнал с амплитудой

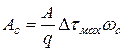(34)

гармоники тактовой частоты ПППИ (частоты дискретизации Ω_д), амплитуды которых равны

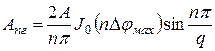(35)

нижние и верхние боковые частоты [четвертое слагаемое (33)] вида с амплитудами

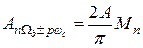(36)

Если модулирующий сигнал занимает полосу частот ω_мин…ω_мах, то нижняя боковая полоса частот около первой гармоники частоты дис­кретизации попадает в полосу частот исходного сигнала [см. (26)].

Как следует из выражения (34) величина амплитуды исходного сигнала в спектре ФИМ сигнала прямо пропорциональна частоте исходного сигнала, что затрудняет демодуляцию ФИМ с помощью фильтра нижних частот, затухание которого в полосе эффективного пропускания должно изменяться по определенному закону, обеспе­чивающему безискаженное восстановление исходного сигнале (реализация такого фильтра вызывает технические трудности).

В спектре ФИМ сигнала амплитуды исходного сигнала значи­тельно (на два-три порядка) меньше, чем при АИМ или ШИМ. По­этому в СП с ВРК на основе фазоимпульсной модуляции принятый канальный сигнал s(t) преобразуют в последовательность импуль­сов с АИМ или ШИМ, из которой при помощи обычного фильтра нижних частот выделяют исходный сигнал. Преобразование ФИМ в ШИМ сопровождается меньшими искажениями по сравнению с преобразованием ФИМ в АИМ. Кроме того, при преобразовании ФИМ в ШИМ Демодулятор оказывается несколько более устойчи­вым по отношению к внешним импульсным помехам. Поэтому на практике чаще применяется демодуляция ФИМ предварительным преобразованием ее в ШИМ.

Для устранения вредного воздействия помех в приемных устрой­ствах систем передачи с ФИМ (как и с ШИМ) применяются ограни­чители амплитуд.

Фазоимпульсная модуляция широко применяется в радиотеле­метрических системах высокой точности и несколько меньше в многоканальных системах радиосвязи.