Классификация систем. Системы разделяют на классы по различным признакам, и в зависимости от решаемых задач выбирают те или иные принципы классификации.
Системы разделяют на классы по различным признакам, и в зависимости от решаемых задач выбирают те или иные принципы классификации.
Примеры классификаций:
1) По виду отображаемого объекта (технические, биологические, социальные, физические, социальные системы и т. п.).
2) По виду научного направления (математические, физические, географические системы и т. п.)
3) Системы делят на открытые и закрытые, детерминированные и стохастические, абстрактные и материальные, и т. д.
Классификации всегда относительны. Так, в детерминированных системах можно найти элементы стохастичности, и, напротив, детерминированную систему можно считать частным случаем стохастической (при вероятности, равной единице). Цель любой классификации – дать рекомендации по выбору методов исследования системы, при этом система может быть охарактеризована некоторыми признаками.
Понятие открытой системы ввёл Л. Фон Берталанфи. Основная черта открытой системы – это способность обмениваться со средой веществом, энергией и информацией. Закрытые системы лишены такой способности (возможны частные случаи, например, если не учитывать процессы обмена веществом и энергией, но учитывать обмен информацией, то говорят об информационно проницаемых и информационно непроницаемых системах).
Понятие цели при изучении систем применимо не всегда, однако при изучении экономических и организационных объектов важно выделять класс целенаправленных, или целеустремлённых систем. В этом классе выделяются системы, в которых цели задаются извне, и системы, в которых цели формируются внутри системы (что характерно для открытых самоорганизующихся систем).
4) Классификация систем по сложности.
Существует несколько подходов к разделению систем по сложности. Есть точка зрения, что большие (по величине, количеству элементов) и сложные (по сложности связей, алгоритмов поведения) системы – это разные классы систем. Пример: классификация К. Боулдинга.
| Тип системы | Уровень сложности | Примеры |
| Неживые системы | Статические структуры | Кристаллы |
| Простые динамические структуры | Часовой механизм | |
| Кибернетические системы с управляемыми циклами обратной связи | Термостат | |
| Живые системы | Открытые системы с самосохраняемой структурой (первая ступень, на которой возможно разделение на живое и неживое) | Клетка |
| Живые организмы с низкой способностью воспринимать информацию | Растение | |
| Живые организмы с более развитой способностью воспринимать информацию | Животное | |
| Системы, характеризующиеся самосознанием, мышлением и нетривиальным поведением | Человек | |
| Социальные системы | Социальная организация | |
| Трансцендентные системы (системы, лежащие в данный момент вне познания исследователя). |
5) По степени организованности и её роли в выборе метода моделирования систем.
а) Представление объекта или процесса принятия решения в виде хорошо организованной системы возможны в том случае, когда исследователю удаётся определить все элементы системы и их взаимосвязи между собой и с целями системы в виде детерминированной зависимости (аналитических, графических).
На представлении этим классом систем основано большинство модулей физических и технических систем. Например, работу сложного механизма приходится отображать в виде упрощённой схемы или систем уравнений, учитывающей не все, а только наиболее существенные с точки зрения автора модели и назначения механизма, элементы и связи между ними. Другой пример: атом может быть представлен в виде планетарной модели, состоящей из ядра и электронов, что упрощает картину, но достаточно для понимания принципов взаимодействия основных элементов, входящих в эту систему.
Таким образом, для отображения сложного объекта в виде хорошо организованной системы приходится выделять существенные и не учитывать относительно несущественные компоненты. При необходимости более детального описания нужно уточнить цель, указав, с какой степенью глубины нас интересует изучаемый объект, и построить новую систему с учётом уточнённой цели.
При представлении объектов или проблемных ситуаций в виде хорошо организованной системы могут использоваться выражения, связывающие цель со средствами (т.е. некий критерий эффективности или целевая функция). Эти выражения могут быть системой уравнений, при этом иногда говорят, что цель представлена в виде критерия функционирования или критерия эффективности.
В большинстве случаев при представлении сложных объектов и проблем на начальных этапах исследования их невозможно представить в виде хорошо организованной системы.
Пример хорошо организованной системы: математическая модель задачи о питании. Пусть хозяйка собирается в магазин за продуктами. Предположим, что в рацион семьи входят 3 различных питательных вещества и требуется их не менее 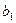 ,
, 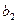 и
и 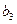 единиц соответственно. В магазине продаётся 5 видов продуктов:
единиц соответственно. В магазине продаётся 5 видов продуктов: 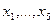 по цене
по цене 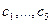 соответственно. Единица продукта
соответственно. Единица продукта 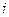 -го вида содержит
-го вида содержит 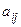 единиц питательного вещества
единиц питательного вещества 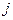 -го вида.
-го вида.
Требуется определить, какое количество продуктов каждого вида следует купить хозяйке, чтобы стоимость продуктов была минимальной, но в рационе семьи содержались все необходимые питательные вещества. Таким образом, целевая функция – минимизировать по 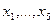 стоимость продуктов:
стоимость продуктов: 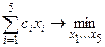 . Условия- ограничения:
. Условия- ограничения: 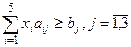 и
и 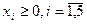 .
.
б) При представлении объекта в виде плохо организованной (диффузной) системы не ставится задача определить все учитываемые компоненты и их связи с целями системы. Система характеризуется некоторым набором макропараметров и закономерностей, которые выявляются на основе исследования не всего объекта или класса явлений, а путём изучения достаточно представительной репрезентативной выборки компонентов (она определяется с помощью некоторых правил), характеризующих исследуемый объект или процесс. На основе такого выборочного исследования получают характеристики или закономерности (стохастические, экономические и др.) и распространяют эти закономерности на поведение системы в целом. При этом делаются соответствующие оговорки, например, при получении статистических закономерностей их распространяют на поведение системы с некоторой вероятностью, которая определяется с помощью специальных методов, изучаемых математической статистикой.
Примером применения диффузной системы является описание газа. При использовании газа для прикладных целей его свойства не определяют путём точного описания поведения каждой молекулы, а характеризуют газ макропараметрами (давление, объем, концентрация и т. д.). Основываясь на этих параметрах, разрабатывают приборы и устройства, использующие свойства газа, не исследуя при этом поведение каждой молекулы.
Отображение объектов в виде диффузных систем используется в следующих случаях:
· при определении пропускной способности систем разного рода
· при определении численности работников в обслуживающих цехах предприятий и учреждениях сферы обслуживания (применяются методы теории массового обслуживания)
· при исследовании потоков информации и документов в организациях.
в) Отображение объектов в виде самоорганизующихся систем позволяет исследовать наименее изученные объекты и процессы с большой неопределённостью на начальном этапе исследования. Класс самоорганизующихся, или развивающихся систем характеризуется рядом признаков и особенностей. Эти особенности обусловлены, как правило, наличием в системе активных элементов и имеют двойственный характер: они являются новыми свойствами, полезными для существования системы, приспосабливаемости её к изменяющимся условиям среды, но в то же время вызывают неопределённость и затрудняют управление системы.
Рассмотрим эти особенности:
· Нестационарность (изменчивость, нестабильность отдельных параметров и стохастичность поведения).
· Уникальность и непредсказуемость поведения системы в конкретных условиях (благодаря наличию активных элементов, у системы появляется наличие свободы, воли, но в то же время появляется и наличие предельных возможностей, определяемых имеющимися ресурсами и структурными связями, характерными для определённого типа систем).
· Способность адаптироваться к изменяющимся условиям среды и помехам (как внешним, так и внутренним), что, казалось бы, является полезным свойством, однако адаптивность может проявляться не только по отношению к помехам, но и по отношению к управляющим воздействиям, что усложняет управление системой.
· Способность противостоять энтропии и тенденциям, разрушающим систему. Эта способность обусловлена наличием активных элементов, осуществляющих обмен веществом, энергией и информацией со средой, благодаря чему в системе не выполняются закономерности увеличения энтропии и даже наблюдаются тенденции самоорганизации и развития.
· Способность вырабатывать варианты поведения и изменять свою структуру при необходимости, сохраняя при этом целостность и основные свойства.
· Способность и стремление к целеобразованию: в отличие от закрытых технических систем, в которых цели задаются извне, в системах с активными элементами цели формируются внутри системы.
· Неоднозначность использования понятий (цель – средства, система – подсистема и т.п.). Эта способность проявляется при формировании структуры цели при разработке проектов сложных автоматизированных комплексов, когда подсистему через некоторое время начинают называть системой, а под целью начинают понимать средства достижения вышестоящих целей.
Часть этих особенностей характерна для диффузных систем (стохастичность поведения, нестабильность отдельных параметров). Важное отличие развивающихся систем с активными элементами от закрытых систем состоит в том, что, начиная с некоторого уровня сложности систему легче изготовить, ввести в действие, преобразовать, чем отобразить формальной моделью.
Основная особенность развивающихся самореализующихся систем – принципиальная ограниченность формализованного их описания. Следовательно, необходимо сочетание формальных методов и методов качественного анализа. В данном классе систем можно выделить подклассы адаптивных (самоприспосабливающихся), самообучающихся и самовосстанавливающихся систем.
Дата добавления: 2016-03-20; просмотров: 944;
