Входные и взаимные сопротивления и проводимости

Принцип наложения формулируется следующим образом: ток в любой ветви схемы равен алгебраической сумме токов частных режимов, вызываемых каждой из ЭДС схемы поочерёдно.

Принцип наложения используется в методе расчета, получившем название метод наложения (суперпозиции).

При расчёте цепей по методу наложения поступают следующим образом: поочерёдно рассчитывают токи от каждой ЭДС, составляя схемы частных режимов, в каждой их которых будет только одна ЭДС, удаляя остальные из схемы, но оставляя в схеме внутреннее сопротивления источников.

Рассчитаем токи в схеме рис. 1-22, используя метод наложения.

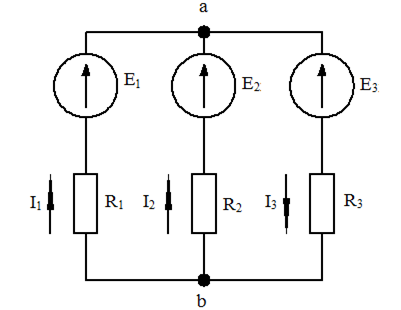
Е₁ = 100 В;

Е₂ = 50 В;

Е₃ = 80 В;

R₁ = 20 Ом;

R₂ = 40 Ом;

R₃ = 60 Ом.

Рис. 1-22. Электрическая схема

Будем считать, что ЭДС Е₁, Е₂, Е₃, идеальны, то есть их внутреннее сопротивление равно нулю.

Составим схему первого частного режима

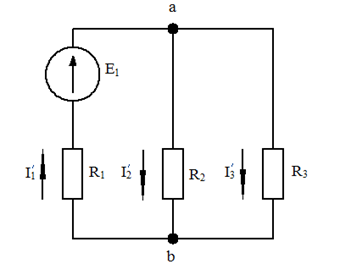
Рис. 1-23. Электрическая схема первого частного режима

Когда в схеме только один ЭДС, то направления токов в ветвях можно сразу точно определить. Так, в схеме рис. 1-23 ток I₁^{`</sup> направлен вверх и определяется по направлению ЭДС Е<sub>1</sub>. Токи I<sub>2</sub><sup>`} и I₃^` будут естественно направлены вниз.

Резисторы R₂ и R₃ соединены параллельно, поэтому ток I₁ будет равен:

I₁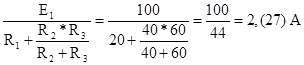^`= . (1-50)

Напряжение U_ab будет меньше ЭДС Е₁ на величину падения напряжения в резисторе R₁:

U_ab^{`</sup>=E<sub>1</sub>-I<sub>1</sub><sup>`}R₁ = 100 – 2,(27)*20 = 54,(54) В . (1-51)

Далее находим токи I₂^{`</sup> и I<sub>3</sub><sup>`}

I₂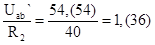^{` =} А; (1-52)

I₃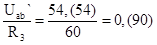^{` =} А. (1-53)

Проверка:

I₁^{`</sup> = I<sub>2</sub><sup>`} +I₃^`= 1,(36) + 0,(90) = 2,(27) А. (1-54)

Теперь составим схему второго частного режима, оставив в схеме ЭДС Е₂ и удалив остальные.

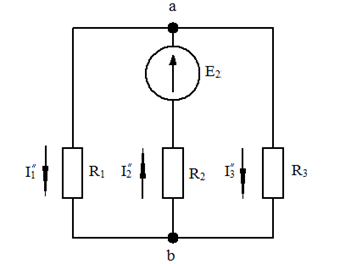
Рис. 1-24. Электрическая схема второго частного режима

Найдем сначала ток I₂^`` :

I₂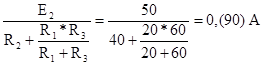^``= ^. (1-55)

Далее найдем напряжение U_ab^`` :

U_ab^{``</sup>=E<sub>2</sub>-I<sub>2</sub><sup>``}R₂ = 50 – 0,(90)*40 = 13,(63) В . (1-56)

А теперь найдём токи I₁^{``</sup> и I<sub>3</sub><sup>``}:

I₁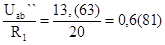^{`` =} А; (1-57)

I₃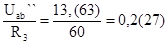^``= А. (1-58)

Проверка:

I₂^{``</sup> = I<sub>1</sub><sup>``} +I₃^``= 0,6(81) + 0,2(27) = 0,(90) А. (1-59)

Составим схему третьего частного режима, оставив ЭДС Е₃ и удалив остальные.

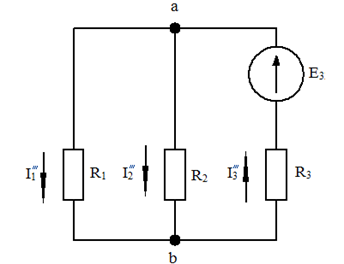
Рис. 1-25 Схема третьего частного режима

Найдем сначала ток I₃^``` :

I₃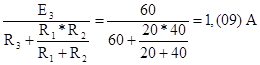^```= (1-60)

Теперь найдем напряжение U_ab^``` :

U_ab^{```</sup>=E<sub>3</sub>-I<sub>3</sub><sup>```}R₃ = 80 – 1,(09)*60 = 14,(54) В. (1-61)

А теперь найдём токи I₁^{```</sup> и I<sub>2</sub><sup>```}:

I₁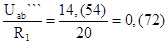^{``` =} А; (1-62)

I₂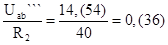^```= А. (1-63)

Проверка:

I₃^{```</sup> = I<sub>1</sub><sup>```} +I₂^```= 0,(72) + 0,(36) = 1,(09) А. (1-64)

Чтобы найти истинные токи в ветвях схемы, сложим алгебраические токи частных режимов. Если направление тока частного режима совпадает с направлением тока в исходной схеме рис. 1-22, то ток частного режима берётся положительным, если не совпадает – отрицательным.

I₁ = I₁^`- I₁^`` -I₁^``` = 2,(27) – 0,6(81) – 0,(72) = 0,8(63)А; (1-65)

I₂ = -I₂^`+ I₂^`` -I₂^``` = -1,(36) + 0,(90) – 0,(36) = -0,(81)А; (1-66)

I₃ = I₃^`+ I₃^`` -I₃^``` = 0,(90) + 0,2(27) – 1,(09) = 0,0(45)А. (1-67)

Так можно рассчитать токи методом наложения, если расчёт производится только один раз.

Если же производится исследование работы схемы, то придётся рассчитывать 40-50 режимов работы схемы с разными значениями ЭДС в ветвях.

Рассмотренный выше метод потребует значительных затрат времени, поскольку эту схему придётся рассчитывать 40-50 раз.

Расчёт значительно сократится, если использовать входные и взаимные проводимости. Дело в том, что если рассчитать все входные и взаимные проводимости один раз, то они будут использоваться при расчёте всех 40-50 режимов работы. От величины ЭДС в ветвях входные и взаимные проводимости не зависят.

Для схемы рис. 1-22 запишем токи в ветвях через входные и взаимные проводимости.

I₁ = E₁g₁₁ – E₂g₁₂ - E₃g₁₃ = I₁^`- I₁^`` - I₁^``` ; (1-68)

I₂ = -E₁g₂₁ + E₂g₂₂ - E₃g₂₃ = -I₂^`+ I₂^`` - I₂^```; (1-69)

I₃ = E₁g₃₁ + E₂g₃₂ - E₃g₃₃ = I₃^`+ I₃^`` - I₃^```. (1-70)

Проводимость – величина обратная сопротивлению, поэтому размерность будет

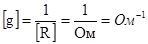=См (Симменс).

В выражении для токов проводимости с одинаковыми индексами g_kk – это входные проводимости схемы относительно разрыва к-ой ветви.

Для схемы рис. 1-23 первого частного режима можно записать:

I₁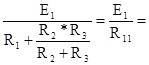^`= Е₁g_11, (1-71)

где R₁₁= 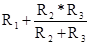- входное сопротивление схемы относительно разрыва в первой ветви;

g₁₁= 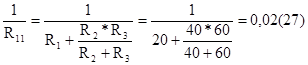См. (1-72)

Это входная проводимость схемы относительно разрыва в первой ветви.

Можно на схеме рис. 1-23 просто убрать источники ЭДС E₁ и относительно этого разрыва определять входные сопротивления и входную проводимость.

Если в выражении (1-71) принять ЭДС Е₁=1В, то можно сказать, что входная проводимость g₁₁ относительно разрыва в первой ветви численно равна току в первой ветви, если в первую ветвь включена ЭДС равная одному вольту.

По схеме рис. 1-23 первого частного режима можно так же определить взаимные проводимости g₂₁ и g_31.

В выражения для токов проводимости с разными индексами g_кn – это взаимные проводимости между к-ой и n-ой ветвями.

В схеме рис. 1-23:

U_ab` = E<sub>1</sub> – I<sub>1</sub>`R₁ ; (1-73)

I₂` = 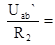E₁g₂₁; g₂₁= 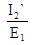; (1-74)

I₃` = 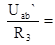E₁g₃₁; g₃₁= 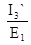. (1-75)

Согласно (1-74) взаимная проводимость g₂₁ между второй и первой ветвью численно равно току второй ветви, если в первой ветви включена ЭДС в один вольт.

Аналогично, взаимная проводимость g₃₁ между третьей и первой ветвью численно равна току третьей ветви, если в первую ветвь включена ЭДС в один вольт.

Таким образом, можно по схеме рис. 1-23 первого частного режима рассчитать токи во всех ветвях. Они будут численно равны входной g₁₁ и взаимным проводимостям g₂₁ и g₃₁, если в первую ветвь включить ЭДС Е₁=1В.

I₁`= 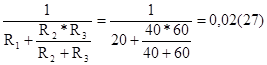А; (1-76)

U_ab` = 1 – I<sub>1</sub>`R₁ = 1 – 0,02(27)*20=0,5(45)В; (1-77)

I₂` = 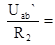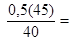0,01(36)А; (1-78)

I₃` = 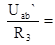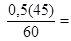0,00(90)А. (1-79)

Проверим первый закон Кирхгофа:

I₁`= I<sub>2</sub>`+ I₃`=0,01(36) + 0,00(90) = 0,02(27)А. (1-80)

Следовательно:

g₁₁=0,02(27) См;

g₂₁=0,01(36) См;

g₃₁=0,00(90) См.

Более того, можно записать формулы для расчёта входной g₁₁ и взаимных проводимостей g₂₁ и g₃₁, по которым сразу можно рассчитать входную и взаимную проводимости:

g₁₁= 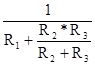; (1-81)

g₂₁= 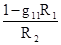; (1-82)

g₃₁= 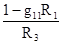. (1-83)

Теперь рассмотрим схему рис. 1-24 второго частного режима. Сразу можно рассчитать входную проводимость g₂₂ относительно разрыва во второй ветви

g₂₂= 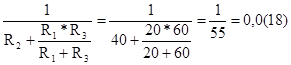См, (1-84)

взаимную проводимость g₁₂ между первой и второй ветвями

g₁₂= 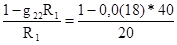=0,01(36) См, (1-85)

взаимную проводимость g₃₂ между третьей и второй ветвями

g₃₂= 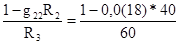=0,00(45) См. (1-86)

Далее рассмотрим схему рис. 1-25 третьего частного режима. Рассчитаем входную проводимость g₃₃ относительно разрыва в третьей ветви

g₃₃= 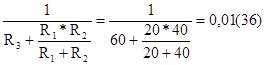См, (1-87)

взаимную проводимость g₁₃ между первой и третьей ветвями

g₁₃= 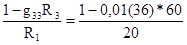=0,00(90) См, (1-88)

взаимную проводимость g₂₃ между второй и третьей ветвями

g₂₃= 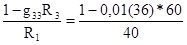=0,00(45) См. (1-89)

Таким образом, найдены все входные и взаимные проводимости в схеме рис. 1-22, причем g₁₂= g₂₁, g₁₃=g₃₁, g₂₃=g₃₂, хотя они определяются разными схемами.

Осталось по формулам (1-68), (1-69), (1-70) рассчитать токи в ветвях схемы рис. 1-22.

Для определения знаков в формулах (1-68), (1-69), (1-70) используем следующее правило: если ток частного режима совпадает по направлению с током в исходной схеме, то произведение ЭДС на проводимости берётся со знаком «плюс», если не совпадает – то со знаком «минус».

Так на схеме рис. 1-23 первого частного режима направление тока I₁` совпадает с направлением тока I₁ в исходной схеме рис. 1-22. Поэтому E₁*g₁₁ в формуле (1-68) взято со знаком «плюс».

Ток I₂` не совпадает с направлением тока I₂ в исходной схеме рис. 1-22. Поэтому E₁*g₂₁ в формуле (1-69) взято со знаком «минус».

Ток I₃` совпадает с направлением тока I₃ в исходной схеме рис. 1-22. Поэтому E₁*g₃₁ в формуле (1-70) взято со знаком «плюс».

Аналогично можно просмотреть расстановку знаков, сравнивая схемы второго и третьего частных режимов с исходной схемой рис. 1-22:

I₁= E₁g₁₁ – E₂g₁₂ – E₃g₁₃= 100*0,02(27)–50*0,01(36)–80*0,00(90) = 0,8(63)А (90)

I₂=-E₁g₂₁ + E₂g₂₂ –E₃g₂₃=-100*0,01(36)+50*0,0(18)–80*0,00(45) = -0,(81)А (91)

I₃= E₁g₃₁ + E₂g₃₂ – E₃g₃₃= 100*0,00(90)+50*0,00(45)–80*0,01(36) = 0,0(45)А(92)

Как видно, результаты расчёта токов через входные и взаимные проводимости точно совпадают с результатами расчёта, когда просто алгебраически складывались токи частных режимов по формулам (1-65), (1-66), (1-67).

Для проверки правильности расчёта найдём мощность источников электрической энергии в схеме рис. 1-22:

P_и=E₁I₁+E₂I₂–E₃I₃=100*0,8(63)+50*(-0,(81))-80*0,0(45)=41,(81) Вт. (1-93)

Далее рассчитаем мощность приемников электрической энергии:

Р_пр=I₁²R₁+ I₂²R₂ + I₃²R₃ = 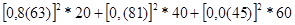= 41,(81) Вт (94)

Как видно мощность источников электрической энергии Р_и равна мощности приемников Р_пр, значит токи рассчитаны верно.

Отметим, что в формуле (1-93) мощность третьего источника ЭДС взята со знаком «минус», потому что в схеме рис. 1-22 направление ЭДС Е₃ и тока I₃ противоположны.