Что такое информатика 12 страница

Задать дополнительные параметры документа можно всего не­сколькими нажатиями мыши, можно добавить верхние и нижние колон­титулы, сноски и закладки. Можно вставить раздел, макет и разрыв страницы из раскрывающегося меню. А внизу страницы показана стати­стика по словам - нажмите на общую сумму слов, чтобы получить под­робные сведения: количество символов, строк, абзацев. Когда же дело доходит до обработки текста, в качестве нового стандарта работы Pages предлагает только самые передовые и интеллектуальные методы.

Набрать текст можно в любой программе. А в Pages его можно зна­чительно улучшить. Теперь вы сможете увидеть документ в полноэкран­ном режиме. Одно нажатие - и ненужные элементы исчезают, вы кон­центрируетесь на том, что пишете, и редактируете, не отвлекаясь. Орга­низуйте свои идеи с помощью режима структуры. Создавайте структуры с несколькими уровнями, разворачивайте или сворачивайте темы, пере­таскивайте элементы, чтобы переместить их на более высокий или низ­кий уровень. Функция автоматической рассылки писем позволяет взять данные или контактную информацию из Адресной книги для создания личных писем, счетов и факсов.

Если вы хотите получить комментарии и обеспечить обратную связь, функция отслеживания изменений сделает взаимодействие про­стым, понятным и точным. Найти нужное место в документе всегда лег­ко: рядом с документом показаны миниатюры всех страниц и разделов, включая сделанные изменения. Можно быстро копировать, перемещать или удалять разделы. Для предварительного просмотра документа мож­но пролистать миниатюры или увеличить их, чтобы просмотреть внима­тельнее.

Pages позволяет легко обмениваться документами с коллегами. Вы можете открывать файлы Microsoft Word в Pages и сохранять документы Pages как файлы Word. Благодаря мощным графическим инструментам и средствам форматирования документы Word отлично выглядят в Pages. Документы Pages можно также сохранять как файлы RTF или в формате простого текста. Или экспортировать их в формат ePub или PDF. Оба этих формата совместимы с приложением iBooks на iPad, iPhone и iPod touch. Документы Pages, Word или PDF можно также от­правлять по электронной почте прямо из Pages, используя приложение Mail, встроенное в Mac OS X.

Используя iBooks, вы можете сохранять и читать документы, соз­данные в приложении Pages на iPhone, iPad и iPod touch. Отчёты и книги с большим количеством текста можно экспортировать в формат ePub - это открытый стандарт, поддерживаемый почти любыми устройствами для чтения электронных книг. Вы можете отправлять документы ePub в приложение iBooks через iTunes, публиковать их в iBookstore или от­правлять по электронной почте коллегам. В iBooks можно выбрать под­ходящую гарнитуру и размер шрифта. Внешний вид текста будет авто­матически преобразован в зависимости от размера экрана и ориентации iPhone, iPad или iPod touch. Документы, насыщенные графикой и имею­щие более сложное форматирование, например новости или брошюры, можно экспортировать как файлы PDF. Файлы в формате PDF всегда выглядят точно так же, как оригинал, вне зависимости от устройства, на котором вы их просматриваете.

6.8 Adobe Acrobat

Adobe Acrobat - пакет программ, выпускаемый компанией Adobe Systems для создания и просмотра электронных публикаций в формате PDF. Существует несколько версий пакета, отличающихся возможно­стями: Adobe Acrobat Standard, Adobe Acrobat Professional, Adobe Acrobat Professional Extended (бывший Adobe Acrobat 3D) и Adobe Acrobat Elements. Разработка Adobe Acrobat Professional Extended прекращена, поддержка для Acrobat 9 Pro Extended продлится до 26 июня 2013 года.

Десятая версия пакета программ Acrobat X вышла в 3-х редакциях: Acrobat X Standard, Acrobat X Pro и Acrobat X Suite. Acrobat Professional, начиная с версии 7.0, содержит в себе Adobe LiveCycle Designer. Acrobat Suite дополнительно содержит: Captivate (включая Media Encoder), Photoshop и Presenter. В версии XI Adobe LiveCycle Designer заменён более упрощённой программой - Adobe FormsCentral.

С версии XI в линейке Acrobat прекращается дальнейшее развитие Acrobat Suite. Пользователям, которым нужны мультимедийные и ком­муникационные функции, предлагается приобрести Adobe eLearning Suite, который содержит в себе все программы, входившие ранее в Acrobat Suite.

Для КПК и коммуникаторов существует версия Adobe Reader for Pocket PC.

6.9 Издательская система LaTeX

Система компьютерной верстки TeX (произносится «тех») была соз­дана выдающимся американским математиком и программистом До­нальдом Кнутом в конце 70-х годов XX века; издательские системы на ее базе до сих пор широко используются и сдавать позиции не собираются. LaTeX (произносится «латех» или «лэйтех», пишется также «LaTeX») - это созданная Лесли Лэмпортом (Leslie Lamport) издательская система на базе TeX-а.

Чем объясняется столь редкое в компьютерном мире долголетие? На первый взгляд, все свидетельствует против TeX^. В самом деле, в отличие, допустим, от популярного ныне Microsoft Word^, TeX не явля­ется системой типа WYSIWYG (What You See Is What You Get): чтобы посмотреть, как будет выглядеть на печати набираемый текст, надо за­пустить отдельную программу. И по структуре файлов TeX несовместим с Word^ (что не удивительно: эта структура мало изменилась с начала 1980-х годов). Наконец, чтобы работать в TeX^, надо потратить опреде­ленное время на его изучение: трудно представить себе книгу под на­званием "TeX for dummies" («TeX для болванов»).

Краткий перечень TeX'овских достоинств:

• Никакая другая из существующих в настоящее время издательских систем не может сравниться с TeX^ в полиграфическом качестве текстов с математическими формулами.

• Система TeX реализована на всех современных компьютерных платформах, и все эти реализации действительно работают оди­наково.

• Благодаря этому TeX стал международным языком для обмена математическими и физическими статьями: набрав свою статью в TeX^, математик может послать ее по электронной почте своему коллеге, даже если отправитель работает под Windows, а получа­тель - с UNIX^ или, допустим, на Макинтоше.

• В Интернете существуют обширные «архивы препринтов», в кото­рые каждый может послать (и из которых каждый может получить) статью; все эти статьи набраны опять-таки в TeX^.

• Наконец, основные реализации TeX^ для всех платформ распро­страняются бесплатно.

Разумеется, у TeX^ есть и недостатки. Главный из них - в том, что с помощью TeX^ тяжело (хотя в принципе и возможно) готовить тексты со сложным расположением материала на странице (наподобие рекламных буклетов). Для таких приложений, практически не встречающихся в на­учно-технической литературе, TeX не предназначен.

Наряду с LaTeX^ распространены также макропакеты Plain-TeX и AMS-TeX. Макропакет Plain-TeX был разработан самим Дональдом Кну­том, рассматривавшим его в качестве платформы для построения более сложных систем; на практике он используется и как средство для обмена текстами (текст, подготовленный для Plain TeX^, сравнительно неслож­но переделать в исходный текст для того же LaTeX^). Что касается AMS-TeX^, то эта издательская система сориентирована на важный, но узкий круг приложений: верстку статей для математических журналов и книг, издаваемых Американским математическим обществом. Соответ­ственно, в AMS-TeX^ предусмотрено большое количество весьма изо­щренных возможностей для создания сложных математических формул, но при этом нет многих вещей, которые естественно было бы ожидать в издательских системах общего назначения (например, автоматической нумерации частей документа). Современные версии LaTeX^ включают в себя AMS-TeX'овские возможности для набора формул (и используются Американским математическим обществом).

6.10 QuarkXPress

QuarkXPress - мощная издательская система, обладающая интуи­тивным интерфейсом и расширенным набором инструментов для обра­ботки текста, управления цветом и графическими элементами и проек­тирования веб-страниц. Программа широко используется в книжных, га­зетных и журнальных издательствах, рекламных и маркетинговых агент­ствах, дизайнерских фирмах и типографиях. Содержит более 160 новых функций и усовершенствований, позволяющих объединить процессы макетирования, проектирования и создания информационного наполне­ния. Благодаря новым функциям, таким как инструменты управления прозрачностью объектов и технология Composition Zones, а также улуч­шенным функциям печати и создания документов в формате PDF, при­ложение обеспечивает полную свободу в процессе проектирования и возможность совместной работы с документами.

Язык интерфейса: Многоязычный (в т.ч. Русский). Тип лицензии: Shareware. Цена: 799.00 USD.

Лекция 7. Алгоритмизация задач

7.1 Типовые решения практических задач

Типовое решение практических задач с привлечением компьютера включает в себя следующие основные этапы:

1. Корректная постановка практической задачи (сбор информа­ции о задаче; точная формулировка условия задачи; определение ко­нечных целей решения; поиск возможных аналогов решения).

2. Формализация задачи (построение математической модели за­дачи; разработка ее структур данных).

3. Разработка алгоритма решения задачи (выбор метода проек­тирования алгоритма, составление алгоритма).

4. Программирование (выбор рабочей среды программирования, программная реализация алгоритма).

5. Совершенствование программного решения (отладка компь­ютерных программ, их проверка на тестовых примерах, уточнение при необходимости математической модели с повторением этапов 2-5).

6. Передача разработанного решения в постоянную эксплуата­цию (документирование всех этапов решения, составление инструкций пользователю, сопровождение задачи в процессе опытной эксплуатации заказчиком).

Важным этапом освоения технологии решения задач на компьюте­ре является развитие навыков разработки алгоритмов, их правильного представления в соответствии с общепринятыми стандартами, знание базовых алгоритмических структур.

Для повышения эффективности применения компьютера как инст­румента решения задач необходимо освоение основной фундаменталь­ной концепции подхода к использованию цифровых вычислительных средств. В информатике таким фундаментом является алгоритмизация возникающих задач. Алгоритмический стиль мышления позволяет свя­зать воедино функционирование информации в конкретной прикладной среде с требованиями обработки информации на компьютере.

Алгоритмическое мышление помогает сформировать следующие основные навыки решения задач:

• умение правильно планировать структуру предстоящих действий для достижения заданной цели при помощи стандартного набора средств;

• строить информационные структуры для описания объектов и процессов в конкретной предметной области;

• правильно организовывать поиск информации, необходимой для решения задачи;

• четко и однозначно формулировать способ решения задачи в общепринятой форме и правильно понимать способ решения, предло­женный другим разработчиком;

• формировать навыки анализа имеющейся информации, умения представлять ее в структурировном виде.

Развитие системного, логического мышления, освоение навыков оперирования формальными понятиями и объектами, характерными для используемых информационных технологий - это тот необходимый уро­вень, который формируется на базе правильного понимания алгоритмов и способов алгоритмизации.

7.2 Понятие алгоритма

Происхождение термина «алгоритм». Слово произошло от имени среднеазиатского ученого Аль-Хорезми (8-9 вв., Хорезм - историческая область на территории современного Узбекистана). В 1857 в библиотеке Кембриджского университета был найден перевод на латинский язык математической работы Аль-Хорезми, в котором имя Аль-Хорезми упо­минается как Алгоритми, откуда и появилось слово «алгоритм». Оно стало особенно употребительным с появлением компьютеров для обо­значения совокупности действий, составляющих какой-либо вычисли­тельный процесс.

Термин «алгоритм» в бытовом понимании. В повседневной жизни выполнение каждой, даже простой задачи обычно осуществляется в не­сколько последовательных этапов (шагов). Например, такую цепочку ша­гов описывает инструкция для получения наличных денег со счета по банковской карте. Подобную инструкцию - четкую последовательность шагов в решении какой-либо жизненной задачи - принято называть ал­горитмом. Каждое отдельное действие - это шаг алгоритма.

Формализация понятия алгоритма, теория алгоритмов. Приведен­ное выше общее описание понятия алгоритма не всегда позволяет сравнить какие-либо две таким образом определенные инструкции. Можно, например, сравнивать два алгоритма решения системы уравне­ний и выбрать из них более подходящий, но невозможно сравнить алго­ритм перехода через улицу с алгоритмом извлечения квадратного корня. С этой целью нужно формализовать понятие алгоритма, т.е. отвлечься от существа решаемой алгоритмом задачи и выделить свойства алго­ритмов, привлекая к рассмотрению только форму их записи.

Задача нахождения единообразной формы записи алгоритмов, ре­шающих различные задачи, является одной из важнейших в теории ал­горитмов. В этой теории предполагается, что каждый шаг алгоритма должен быть таков, что его может выполнить достаточно простое уст­ройство (например, машина). Так, для уточнения понятия «алгоритм» и получения возможности математического исследования алгоритмов в 30-х гг. ХХ века были предложены абстрактные вычислительные маши­ны - машина Поста и машина Тьюринга. Эти механизмы, обладающие свойствами универсальности и простоты своей логической структуры, позволили решить проблему существования алгоритма решения любой практической задачи. В частности, было доказано, что если для решения задачи можно построить машину Поста-Тьюринга, то такая задача алго­ритмически разрешима. Также была доказана возможность существова­ния математических задач, для решения которых вообще не может су­ществовать никакой алгоритм.

Вычислительный алгоритм. Это упорядоченный набор основных ма­тематических и логический действий, однозначно определяющий про­цесс перехода от допустимых исходных данных задачи к конечному ре­зультату ее решения и обладающий свойствами массовости, конечно­сти, определенности, детерминированности. Основные особенности вы­числительных алгоритмов состоят в следующем.

Массовость - это возможность применять многократно один и тот же алгоритм к различным вариантам его исходных данных. Алгоритм служит, как правило, для решения не одной конкретной задачи, а не­которого класса задач. Так алгоритм сложения столбиком применим к любому конечному набору натуральных чисел. Для каждого алгоритма есть некоторое множество объектов, допустимых в качестве исходных данных. Например, в алгоритме деления вещественных чисел дели­мое может быть любым, а делитель - тоже любым, но за исключением нуля.

Конечность - это обязательное наличие искомого результата по­сле завершения алгоритма либо четкая фиксация причины, по которой результат не мог быть получен. Следует отметить, что на практике встречаются примеры формально бесконечных алгоритмов, например алгоритм обработки данных системы абонентских пунктов банка. Этот алгоритм состоит в непрерывном повторении цепочки действий («идентифицировать клиента», «зафиксировать запрос клиента на транзакцию», «проверить допустимость транзакции», «выполнить транзакцию» и т.д.), выполняемых с определенной частотой (через каждую секунду, минуту, час) во все время функционирования данной банковской системы.

Определенность - это наличие на каждом шаге алгоритма у испол­нителя достаточной информации для того, чтобы его можно было вы­полнить. Исполнителю также нужно четко знать, каким именно образом этот шаг выполняется. Сами шаги инструкции должны быть достаточно простыми, а исполнитель должен однозначно понимать смысл каждого из действий, составляющих алгоритм (например, при вычислении корней квадратного уравнения он должен понимать смысл вычисления дискри­минанта).

Детерминированность - это отсутствие элементов случайности при выполнении алгоритма. При многократном применении алгоритма к од­ним и тем же исходным данным должен получаться всегда один и тот же результат. Поэтому, например, процесс преобразования информа­ции, в котором участвует бросание монеты, не может быть назван алгоритмом.

7.3 Формы представления алгоритмов

Для записи алгоритма могут использоваться различные формы его представления.

Вербальная форма представления алгоритма предполагает запись алгоритма на русском языке (или любом другом естественном языке) в виде последовательности пронумерованных инструкций. Как правило, эта форма записи алгоритма громоздка, неудобна и недостаточно на­глядна.

Например, в ней описание алгоритма нахождения НОД (наиболь­шего общего делителя) двух целых положительных чисел m и n может быть представлено в виде последовательности следующих четырех шагов:

Шаг 1: Сравнить m и n.

Шаг 2: Если m равно n, то m и есть исходный НОД, расчет окончен. Иначе перейти к шагу 3.

Шаг 3: Если m больше n, то уменьшить значение m на величину n и вернуться к шагу 1. Иначе перейти к шагу 4.

Шаг 4: Уменьшить значение n на величину m и вернуться к шагу 1.

7.4 Запись алгоритма

Эта современная запись алгоритма нахождения НОД - весьма уп­рощенная. Запись, данная первоначально Евклидом, заполняет целую страницу текста, причем последовательность элементарных действий там значительно сложней.

Представление алгоритма в форме блок-схемы реализуется в ви­де набора геометрических элементов (блоков), соединенных стрелка­ми. Каждый блок - это «шаг» алгоритма, его отдельное действие. На­правление стрелок между блоками задает последовательность дейст­вий. В табл. 4 представлены основные стандартные элементы блок - схем.

Элементы блок-схемы различаются по своему внешнему виду и на­значению. Так, элементы, содержащие инструкции по каким-либо преоб­разованиям величин, обозначаются прямоугольниками, а элементы, со­держащие проверку условий, - ромбами. Операции ввода-вывода дан­ных обозначаются параллелограммами. Начало и конец алгоритма обо­значаются прямоугольниками с двумя скругленными противоположными сторонами, внутри которых пишут: «начало» или «конец» соответственно.

Из прямоугольника выходит единственная стрелка, входить в него может несколько стрелок. Из обеих острых вершин ромба выходят стрелки: одна из них помечается словом «да», другая - словом «нет», они задают дальнейшее направление вычислений в случае, соответст­венно, выполнения или невыполнения записанного внутри ромба усло­вия.

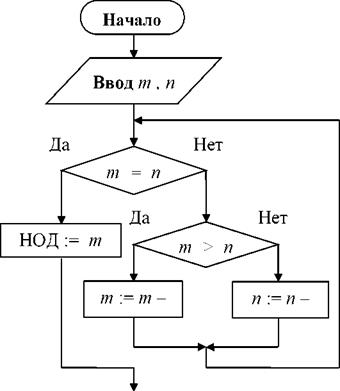
Назначение и правила использования всех типов блоков приведены в табл. 4 в графах Название элемента и Пояснение. С использованием приведенных в табл. 4 стандартных элементов вышеуказанный алго­ритм нахождения НОД двух положительных целых чисел m и n примет вид блок-схемы на рис. 6. Внутри блоков в ней знаком := обозначена операция присваивания переменной величине, указанной слева от зна­ка, ее значения, вычисляемого по формуле, стоящей справа от знака.

Вывод НОД

Конец

Рис. 6. Блок-схема алгоритма
нахождения НОД

Представление алгоритма в форме псевдокода основано на описании этапов решения задачи с помощью ограниченного набора стандартных синтаксических конструкций. В псевдокоде, в частности, могут использо­ваться отдельные инструкции формальных алгоритмических языков про­граммирования. Например, возведение X в степень A обозначается как X**A, извлечение квадратного корня из X обозначается как Sqrt (X).

Так же как в формальных языках программирования, в псевдокоде присутствуют ключевые слова, смысл которых заранее оговорен и фик­сирован. В табл. 5 приведен базовый перечень ключевых слов.

В качестве ключевых могут использоваться также соответствующие английские слова-аналоги: else вместо иначе, then вместо то.

В самом общем виде запись алгоритма в форме псевдокода выгля­дит следующим образом:

алг название алгоритма (аргументы - входные параметры и пара­метры - результаты работы алгоритма) дано | условия применимости алгоритма надо | цель выполнения алгоритма нач описание промежуточных (внутренних) величин алгоритма команда 1; команда 2;

команда N кон

Здесь часть записи от слова алг до слова нач называется заголов­ком алгоритма, а часть, заключенная между словами нач и кон, - его телом. Внутри тела также могут встречаться слова нач и кон, группа ко­манд между ними образует свой отдельный блок команд. Команды от­деляются друг от друга символом «;».

Сразу после названия алгоритма в круглых скобках указываются ха­рактеристики (арг или рез) и тип значения (цел, вещ, сим, лог или таб) всех входных (арг) и выходных (рез) величин. При описании массивов служебное слово таб дополняется граничными парами значений по каж­дому индексу элементов массива.

В конце любой строки в текст псевдокода после знака «|» можно вставлять комментарий, облегчающий понимание алгоритма.

Разделы «дано» и «надо» в записи алгоритма не являются обяза­тельными.

К числу основных действий, составляющих тело алгоритма, отно­сятся команды ввода-вывода, присваивания, перехода, ветвления и циклов. Для обозначения этих команд используются соответствующие ключевые слова.

Команда ввода: ключевое слово ввод, за которым указываются имена переменных, для которых вводятся значения. Например, команда ввод a,b,c означает ввод значений соответственно для переменных a,b,c.

Команда вывода: ключевое слово вывод, за которым следуют имена выводимых переменных, выводимые выражения и тексты (тексты помещаются в кавычки). Например, команда вывод "S = ", S означает вывод имени переменной S, за которым после знака равенства = следу­ет вывод текущего значения этой переменной.

Команды присваивания используются для вычисления выражений и присваивания их значений переменным. Общий вид команды: "пере­менная" := "выражение", где знак означает команду замены преж­него значения переменной, стоящей в левой части, на вычисленное зна­чение выражения, стоящего в правой части.

Например, команда x := у + z означает присваивание переменной x значения суммы величин у и z, а команда k := k+1 означает увеличение текущего значения переменной k на единицу.

Команда перехода: ключевые слова идти к, после которых указы­вается номер той строки, команда которой должна выполняться сле­дующей. Таким образом, команда перехода изменяет естественную по­следовательность выполнения команд по возрастанию номеров строк. Например, записанная в 5-й строке команда идти к 10 означает, что да­лее должна выполняться команда, записанная в 10-й строке, а не ко­манда, записанная в следующей 6-й строке.

Для организации ветвлений вычислительного процесса применяют­ся команды, начинающиеся с ключевых слов если и выбор, цикличе­ские вычисления организуются с помощью команд, начинающихся с ключевых слов пока и для. Подробно эти команды рассмотрены далее при описании базовых структур алгоритмов.

С использованием псевдокода вышеуказанный алгоритм нахожде­ния НОД двух положительных целых чисел m и n примет следующий вид:

1. алг Наибольший Общий Делитель (арг цел m, n, рез цел nod)

2. дано | положительные целые числа m, n

3. надо | nod - наибольший общий делитель чисел m, n

4. нач

5. ввод m, n;

6. если m = n то идти к 9 все;

7. если m > n то m := m - n иначе n := n - m все;

8. идти к 6;

9. nod := m;

10. вывод “Значение НОД равно”, nod

11. кон

Эта форма представления облегчает запись алгоритма на стадии его проектирования и дает возможность в дальнейшем легко перевести алгоритм в более широкий набор команд формального языка програм­мирования.

7.5 Базовые структуры алгоритмов

Алгоритм решения любой вычислительной задачи можно описать, используя комбинации из следующих трех стандартных базовых конст­рукций алгоритмов:

• последовательного алгоритма - алгоритма линейной структуры;

• ветвящегося алгоритма - алгоритма разветвляющейся структуры;

• циклического алгоритма - алгоритма циклической структуры.

Алгоритм линеинои структуры - это объединение всех действии в единую цепь, в которой каждое последующее действие строго и одно­значно следует за предыдущим действием (рис.7). На языке псевдокода соответствующая последовательность команд запишется в виде:

команда 1; команда 2;. . .; команда N

Алгоритм разветвляющейся структуры содержит проверку одного либо нескольких условий, по результатам которых происходит переклю­чение на один из возможных двух либо один из возможных нескольких вариантов дальнейшего развития процесса. Различают четыре вида ветвящегося алгоритма.

Ветвление «если-то-иначе» (рис. 8) встречается на практике наибо­лее часто. В нем присутствует проверка одного условия, по результатам которой происходит выбор между двумя возможными цепочками даль­нейших действий.

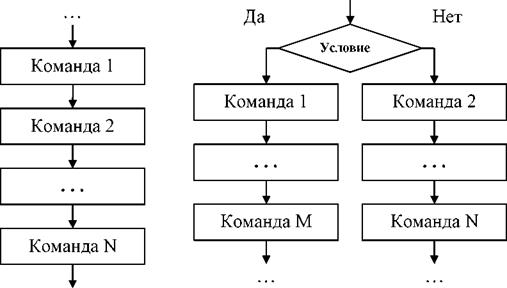Рис. 7. Алгоритм Рис. 8. Алгоритм линейной структуры разветвляющейся структуры (вариант «если-то-иначе»)

На языке псевдокода соответствующая последовательность ко­манд запишется в виде: если Условие

то команда 1;. . .; команда M иначе команда 2;...; команда N все

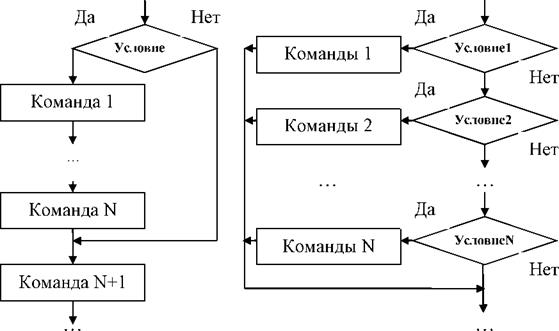
Ветвление «если-то» (рис. 9) позволяет при соблюдении проверяе­мого в нем условия выполнить заданную цепочку действий: команды 1...N. При несоблюдении указанного условия команды 1...N пропускаются и сразу начинает выполняться следующая за ветвлением команда N+1.

На языке псевдокода вариант «если-то» запишется в виде: если Условие

то команда 1;. . .; команда N все;

команда N+1;