Оценка скорости программ

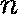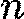
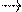
Временна́я сложность — одна из важнейших характеристик алгоритма. В то же время точная зависимость числа выполняемых в нём операций от параметра (длины массива, номера элемента последовательности и т.п.) часто трудно находима. Почти всегда, однако, не так сложно определить асимптотику роста времени выполненияалгоритма при неограниченном увеличении параметра (когда ). Все функции, которые будут нами рассматриваться далее, явля-ются асимптотически неотрицательными функциями натурального аргумента, то есть

Эта аналогия, однако, не является полной. Некоторые свойства числовых отношений не выполняются для их функциональных аналогов.

Оценки времени исполнения. Cимвол O()

Для оценки производительности алгоритмов можно использовать разные подходы. Самый бесхитростный - просто запустить каждый алгоритм на нескольких задачах и сравнить время исполнения. Другой способ - математически оценить время исполнения подсчетом операций. Рассмотрим алгоритм вычисления значения многочлена степени n в заданной точке x. P_n(x) = a_nxⁿ + a_n-1x^n-1 + ... + a_ixⁱ + ... + a₁x¹ + a₀ Алгоритм 1 - для каждого слагаемого, кроме a₀ возвести x в заданную степень последовательным умножением и затем домножить на коэффициент. Затем слагаемые сложить. Вычисление i-го слагаемого(i=1..n) требует i умножений. Значит, всего 1 + 2 + 3 + ... + n = n(n+1)/2 умножений. Кроме того, требуется n+1 сложение. Всего n(n+1)/2 + n + 1= n²/2 + 3n/2 + 1 операций. Алгоритм 2 - вынесем x-ы за скобки и перепишем многочлен в виде P_n(x) = a₀ + x(a₁ + x(a₂ + ... ( a_i + .. x(a_n-1 + a_nx))). Например, P₃(x) = a₃x³ + a₂x² + a₁x¹ + a₀ = a₀ + x(a₁ + x(a₂ + a₃x)) Будем вычислять выражение изнутри. Самая внутренняя скобка требует 1 умножение и 1 сложение. Ее значение используется для следующей скобки... И так, 1 умножение и 1 сложение на каждую скобку, которых.. n-1 штука. И еще после вычисления самой внешней скобки умножить на x и прибавить a₀. Всего n умножений + n сложений = 2n операций. Зачастую такая подробная оценка не требуется. Вместо нее приводят лишь асимптотическую скорость возрастания количества операций при увеличении n. Функция f(n) = n²/2 + 3n/2 + 1 возрастает приблизительно как n²/2 (отбрасываем сравнительно медленно растущее слагаемое 3n/2+1). Константный множитель 1/2 также убираем и получаем асимптотическую оценку для алгоритма 1, которая обозначается специальным символом O(n²). Это - верхняя оценка, т.е количество операций(а значит, и время работы) растет не быстрее, чем квадрат количества элементов. Чтобы почувствовать, что это такое, посмотрите на таблицу, где приведены числа, иллюстрирующие скорость роста для нескольких разных функций.

n	log n	n*log n	n²


		2,048	65,536
4,096		49,152	16,777,216
65,536		1,048,565	4,294,967,296
1,048,576		20,969,520	1,099,301,922,576
16,775,616		402,614,784	281,421,292,179,456

Если считать, что числа в таблице соответствуют микросекундам, то для задачи с n=1048576 элементами алгоритму с временем работы O(log n)потребуется 20 микросекунд, алгоритму со временем O(n) - 17 минут, а алгоритму с временем работы O( n² ) - более 12 дней... Теперь преимущество алгоритма 2 с оценкой O(n) перед алгоритмом 1 достаточно очевидно.

Наилучшей является оценка O(1)...В этом случае время вообще не зависит от n, т.е постоянно при любом количестве элементов.

Таким образом, O() - "урезанная" оценка времени работы алгоритма, которую зачастую гораздо проще получить, чем точную формулу для количества операций.

Итак, сформулируем два правила формирования оценки O().

При оценке за функцию берется количество операций, возрастающее быстрее всего.
То есть, если в программе одна функция, например, умножение, выполняется O(n) раз, а сложение - O(n²) раз, то общая сложность программы - O(n²), так как в конце концов при увеличении n более быстрые ( в определенное, константное число раз ) сложения станут выполнятся настолько часто, что будут влиять на быстродействие куда больше, нежели медленные, но редкие умножения. Символ O() показывает исключительно асимптотику!

При оценке O() константы не учитываются.
Пусть один алгоритм делает 2500n + 1000 операций, а другой - 2n+1. Оба они имеют оценку O(n), так как их время выполнения растет линейно.

В частности, если оба алгоритма, например, O( n*log n ), то это отнюдь не значит, что они одинаково эффективны. Первый может быть, скажем, в 1000 раз эффективнее. O() значит лишь то, что их время возрастает приблизительно как функция n*log n.

Другое следствие опускания константы - алгоритм со временем O(n²) может работать значительно быстрее алгоритма O(n) при малых n... За счет того, что реальное количество операций первого алгоритма может быть n² + 10n + 6, а второго - 1000000n + 5. Впрочем, второй алгоритм рано или поздно обгонит первый... n² растет куда быстрее 1000000n.

Основание логарифма внутри символа O() не пишется.
Причина этого весьма проста. Пусть у нас есть O( log₂n). Но log₂n=log₃n/log₃2, а log₃2, как и любую константу, асимптотика - символ О() не учитывает. Таким образом, O( log₂n) = O( log₃n).

К любому основанию мы можем перейти аналогично, а значит и писать его не имеет смысла.

12 3

Дата добавления: 2016-03-20; просмотров: 1081;