Дифракция световых волн: принцип Гюйгенса-Френеля 5 страница

Формирование дифракционной картины при наклонном падении плоской монохроматической световой волны на отражательную дифракционную решётку

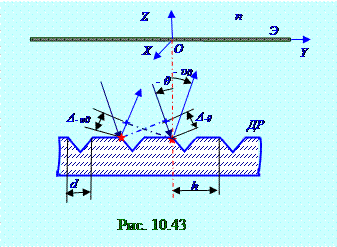
После паденияпараллельнымпучком световой волныв однородной изотропной среде с

n показателем преломления(рис. 10.41) под +θуглом падениянаповерхность

ДРдифракционной решётки, имеющей форму Шштрихов бесконечной длины по перпендикулярнойплоскости чертежа OX оси, dширинойпо OY оси и h расстоянием между штрихами, оптическая Δ_+υ-m разность хода двух отражённых параллельныхлучей,отстоящихдруг от другана h расстоянии и имеющих +υ_-m угол между направлением лучей и нормальюк поверхностиДРдифракционной решёткиимеет с учётом (10.147) следующий вид: Δ_+υ-m = hsin(+υ_-m), (10.176)

где знак "+" плюс означает, что +υ_-m угол отсчитывается от нормалик поверхности

ДРдифракционной решёткипротив"часовой стрелки".

Оптическая Δ_+θ разность хода двух параллельныхлучей,падающих (рис. 10.41) под

+θ угломотносительнонормалик поверхностиДРдифракционной решётки, отстоящимидруг от другана h расстоянии, имеет с учётом (10.147) следующий вид: Δ_+θ = hsin(+θ). (10.177)

Общая оптическая Δ_o+θ разность хода двух параллельныхлучей, падающих (рис. 10.2.0.41) под+θ угломотносительнонормалик поверхностиДРдифракционной решётки, и отражённых от

N щелей в виде вторичнойсферическая волна под +υ_-m углом, имеет с учётом (10.176), (10.177) следующий вид: Δ_o+θ = Δ_+θ - Δ_+υ-m = hsin(+θ) - hsin(+υ_-m), (10.178) где знак "-" минус присутствует потому, что левыйиз падающих (рис. 10.41) под +θ угломотносительнонормалик поверхностиДРдифракционной решётки световых лучей на величину Δ_+θ имеет бόльшую оптическую длину по сравнению с правымсветовым луч, а правый изотражённых от N щелей в виде вторичнойсферической волны под +υ_-m углом световых лучей на величину Δ_+υ-m имеет бόльшую оптическую длину по сравнению с левымсветовым лучом.

Условие наблюдение главного дифракционного максимумаm - ого порядка (рис. 10.41) на

Э экране от отражённых параллельныхпучков световой волныв однородной изотропной среде с

n показателем преломления,которыеобразуются от падения световыхлучейпод +θугломнаповерхностьДРдифракционной решётки,имеет с учётом (10.178) следующий вид:

Δ_o+θ = hsin(+θ) - hsinυ_imax= ± mλ, (10.179) где υ_imax - i - ое значение угла отражённых параллельныхпучков к главной оптической осиЛ линзы, под которым при данной λ длине волны производят наблюдение главного дифракционного максимумаm - ого порядка.

Условие наблюдение главного дифракционного максимума0 - ого порядка (рис. 10.42) на

Э экране от отражённых параллельныхпучков световой волныв однородной изотропной среде с

n показателем преломленияимеет с учётом (10.179) следующий вид:

Δ_o+θ = hsin(+θ) - hsin(+υ₀) = 0 ↔ +θ =+υ₀, (10.180)

где+υ₀ - значение угла к главной оптической осиЛ линзы, под которым при данной λ длине волны производят наблюдение главного дифракционного максимума0 - ого порядка, которое равно +θуглу падениянаповерхностьДРдифракционной решётки параллельногопучка световой волныв однородной изотропной среде с n показателем преломления.

Условие наблюдение главного дифракционного максимума"- m" порядка (рис. 10.41) на

Э экране от отражённых параллельныхпучков световой волныв однородной изотропной среде с

n показателем преломленияимеет с учётом (10.181) следующий вид:

Δ_o+θ = hsin+θ - hsin(+υ_-m)= - mλ ↔ sin(+υ_-m) =(mλ/h) + sin(+θ), (10.181)

где+υ_-m > 0 - значение угла, отсчитываемое от нормалик поверхностиДРдифракционной решёткипротив"часовой стрелке", под которым при данной λ длине волны производят наблюдение главного дифракционного максимума"- m" порядка, наблюдаемого на Э экране в отрицательной области

OY оси; m - модуль порядка главного дифракционного максимума.

Условие наблюдение главного дифракционного максимума"+ m" порядка (рис. 10.41) на

Э экране от отражённых параллельныхпучков световой волныв однородной изотропной среде с

n показателем преломленияимеет с учётом (10.178) следующий вид:

Δ_o+θ = hsin+θ - hsin(υ_+m)= mλ ↔ sin(υ_+m) = sin(+θ) - (mλ/h), (10.182)

где υ_+m > 0 - значение угла, отсчитываемое от нормалик поверхностиДРдифракционной решёткипротив"часовой стрелке", если в (10.184) sin(+θ) > mλ/h и тогда наблюдение главного дифракционного максимума"+ m" порядка наблюдается на Э экране в отрицательной области

OY оси; υ_+m < 0 - значение угла, отсчитываемое от нормалик поверхностиДРдифракционной решёткипо"часовой стрелке", если в (10.182) sin(+θ) < mλ/h и тогда наблюдение главного дифракционного максимума"+ m" порядка наблюдается на Э экране в положительной области

OY оси; m - модуль порядка главного дифракционного максимума.

Условие наблюдение главного дифракционного максимумаm - ого порядка (рис. 10.44) на

Э экране от отражённых параллельныхпучков световой волныв однородной изотропной среде с

n показателем преломления,которыеобразуются от падения световыхлучейпод -θугломнаповерхностьДРдифракционной решётки,имеет с учётом (10.182) следующий вид:

Δ_o-θ = hsin(-θ) - hsinυ_imax= ± mλ, (10.183)

где υ_imax - i - ое значение угла к главной оптической осиЛ линзы, под которым при данной λ длине волны производят наблюдение главного дифракционного максимумаm - ого порядка.

Условие наблюдение главного дифракционного максимума0 - ого порядка (рис. 10.44) на

Э экране от отражённых параллельныхпучковсветовой волныв однородной изотропной среде с

n показателем преломленияимеет с учётом (10.183) следующий вид:

Δ_o-θ = hsin(-θ) - hsin(-υ₀) = 0 ↔ -θ =-υ₀, (10.184)

где -υ₀ <0 - значение угла, отсчитываемое от нормалик поверхностиДРдифракционной решёткипо"часовой стрелке", под которым при данной λ длине волны производят наблюдение главного дифракционного максимума0 - ого порядка, которое равно -θ углу падениянаповерхностьДРдифракционной решётки параллельногопучка световой волныв однородной изотропной среде с n показателем преломления.

Условие наблюдение главного дифракционного максимума"+ m" порядка (рис. 10.44) на

Э экране от отражённых параллельныхпучковсветовой волныв однородной изотропной среде с

n показателем преломленияимеет с учётом (10.183) следующий вид:

Δ_o-θ = hsin(-θ) - hsin(-υ_+m)= mλ ↔ sin(-υ_+m) = sin(-θ) - (mλ/h), (10.185)

где+υ_-m < 0 - значение угла, отсчитываемое от нормалик поверхностиДРдифракционной решёткипо"часовой стрелке", под которым при данной λ длине волны производят наблюдение главного дифракционного максимума"+ m" порядка, наблюдаемого на Э экране в положительной области

OY оси; m - модуль порядка главного дифракционного максимума.

Условие наблюдение главного дифракционного максимума"- m" порядка (рис. 10.44) на

Э экране от отражённых параллельныхпучковсветовой волныв однородной изотропной среде с

n показателем преломленияимеет с учётом (10.183) следующий вид:

Δ_o-θ = hsin(-θ) - hsin(υ_-m)= -mλ ↔ sin(υ_-m) = sin(-θ) + (mλ/h), (10.186)

где - υ_-m < 0 - значение угла, отсчитываемое от нормалик поверхностиДРдифракционной решёткипо "часовой стрелке", если с учётом sin(-θ) < 0 в (10.188) |sin(+θ)| > mλ/h и тогда наблюдение главного дифракционного максимума"- m" порядка наблюдается на Э экране в положительной области OY оси; υ_-m > 0 - значение угла, отсчитываемое от нормалик поверхностиДРдифракционной решёткипротив"часовой стрелке", если с учётом sin(-θ) < 0 в (10.186) |sin(+θ)| < mλ/h и тогда наблюдение главного дифракционного максимума"+ m" порядка наблюдается на Э экране в отрицательной области OY оси; m - модуль порядка главного дифракционного максимума.

Спектральные характеристики дифракционных решеток: угловая и линейная дисперсия

Согласно (10.161) выражению нехроматическая световая волна, т.е. состоящая из дискретного k количестваλ_k длин световых волн,после прохожденияпараллельнымпучком нормальнок поверхностиДРдифракционной решёткис Nщелямиdшириной, расстояние между которыми равно h, будет иметь вдифракционной картине(рис. 10.37) дифракционные максимумыпод

υ_maxk углами к главной оптической осиЛ линзы. При этом каждая λ_k длина световой волны будет иметь дифракционный максимум нулевого порядка при (10.161) m = 0, расположенный в центре (рис. 10.2.0.37) Э экрана, т.е. дифракционные максимумы нулевого порядка от каждой λ_k длинынехроматической световой волны будут совпадать по месту расположения на Э экране.

Дифракционные максимумы1-го, 2-го, 3-го и т.д. порядков при (10.149) соответственно

m = 1 и m = -1, m = 2 и m = -2 , m = 3 и m = -3 и т.д. будут для каждой λ_k длины нехроматической световой волны иметь свои углы отклонения к главной оптической осиЛ линзы: - υ_max11, υ_max12, υ_max13,…. - углы отклонения к главной оптической осиЛ линзы (рис. 10.37)дифракционных максимумов1-го, 2-го, 3-го и т.д. порядков для λ₁ длины световой волны;

- υ_max21, υ_max22, υ_max23,…. - углы отклонения к главной оптической осиЛ линзы(рис. 10.37)дифракционных максимумов1-го, 2-го, 3-гои т.д. порядков для λ₂ длины световой волны;

- υ_max31, υ_max32, υ_max33,…. - углы отклонения к главной оптической осиЛ линзы(рис. 10.37)дифракционных максимумов1-го, 2-го, 3-гои т.д. порядков для λ₃ длины световой волны и т.д. Способность ДРдифракционной решётки образовывать дифракционные максимумына

Э экране (рис. 10.37) под углами отклонения к главной оптической оси Ллинзы, зависящими от

λ_k длинысветовой волны, называют спектральным свойствомДРдифракционной решётки.

От ДРдифракционной решётки вторичнаясферическая волна, имеющая световые волны с длинами λ и λ+δλ, гдеλ= λ₀ /n–длинасветовой волны в однородной изотропной среде с

n показателем преломления, поэтому оптическаяλ = λ₀ /nдлинаэтой световой волны совпадает с геометрическими размерами на рис. 10.45, распространяются от каждой из N щелейпод υ_imaxλ и υ_imaxλ+δλ углами к главной оптическойOZ осиЛ линзы.

Параллельные пучкикаждой световой волны с длинами λ и λ+δλ, фокусируется Л линзойв еёфокальнойплоскости c f расстоянием на Э экране. Главный дифракционный максимумдля

λдлинысветовой волны образуется под υ_imaxλ угломотклонения к главной оптическойOZ осиЛ линзы,а главный дифракционный максимумдляλ+δλ длины световой волны образуется под υ_imaxλ+δλ угломотклонения к главной оптическойOZ осиЛ линзы. При этом υ_imaxλ+δλ уголбольшеυ_imaxλ угла, т.к. с учётом (10.163)дифракционные максимумы1-го, 2-го, 3-го и т.д. порядков, которые наблюдаются на Э экране под υ_imax углами к главной оптической осиЛ линзы, для λ и λ+δλ длин световой волны соответствуют следующим соотношениям:

|sinυ_imaxλ| = mλ/h; |sinυ_imaxλ+δλ | = m(λ+δλ)/h. (10.187)

где υ_imax, υ_imaxλ+δλ - i - ое значение угла (рис. 10.2.0.37) к главной оптической осиЛ линзы, под которым при данных λ и λ+δλ длинах световых волн производят наблюдение главных дифракционных максимумовm - ого порядка, имеющее одинаковое значение для этих λ и λ+δλ длин световых волн.

изменении длины световой волны на δλ величину, которая определяется из следующего соотношения: D_у = δυ/δλ. (10.189) Элементарное δ(hsinυ_imax) приращение с использованием левой части (10.149) при изменении υ_imax углаотклонения к главной оптическойOZ осиЛ линзыглавного дифракционного максимумана элементарную δυ величину имеет следующий вид:

δ(hsinυ_imax) = h(dsinυ/dυ)| _{υ= υi max}δυ = (hcosυ_imax)δυ.(10.190) Элементарное δ(hsinυ_imax) приращение с использованием правой части (10.149) при изменении длины λ световой волны, распространяющейся (рис. 10.37) от каждой из N щелейпод υ_imax углом к главной оптическойOZ осиЛ линзы, на элементарную δλ величину без учёта отрицательногознака в этой правой части имеет следующий вид: δ(hsinυ_imax) = δ(mλ) = m(dλ/dλ)δλ = mδλ.(10.191) Приравниваем (10.190) и (10.191) и получаем с учётом (1.189) зависимость угловойD_удисперсииДРдифракционной решёткис учётом малыхυ_imax угловотклонений к главной оптическойOZосиЛ линзыглавных дифракционных максимумов, поэтому cosυ_imax ≈ 1, от номера порядка m =1, 2, 3, …дифракционных максимумови h расстояниямежду щелями дифракционной решётки, которая имеет следующий вид:

(hcosυ_imax)δυ = mδλ ↔ δυ/δλ = m/(hcosυ_imax) ↔ D_у = m/(hcosυ_imax) ≈ m/h.(10.192)

ЛинейнаяD_лдисперсия- это отношениеприращения (рис. 10.45)линейного δl отклонения к главной оптическойOZ осиЛ линзыглавного дифракционного максимумаm - го порядка при изменении длины световой волны на δλ величину, которая определяется из следующего соотношения: D_л = δl/δλ.(10.193) C учётом (рис. 10.45) малыхυ_imax угловотклонений к главной оптическойOZ осиЛлинзыглавных дифракционных максимумов линейное δl отклонение относительно этой главной оптическойOZ оси Л линзыглавного дифракционного максимумаm - го порядка при изменении длины световой волны на δλ величину определяется из следующего соотношения: δl ≈ fδυ. (10.194) Подставляем (10.194) в (10.193) и получаем следующую зависимостьD_ллинейной дисперсииот fфокусного расстояния Л линзы, которое равно расстоянию от этой Л линзы до Э экрана, а также в зависимостиот (10.189) угловойD_удисперсииДРдифракционной решётки: D_л ≈ fδυ/δλ ↔ D_л ≈ fD_у.(10.195) Подставляем (10.192) выражение угловойD_удисперсииДРдифракционной решёткив (10.197) и получаем следующуюзависимость линейнойD_лдисперсии от fфокусного расстояния Л линзы, которое равно расстоянию от этой Л линзы до Э экрана,а также в зависимости от номера порядка m =1, 2, 3, …дифракционных максимумови h расстояниямежду щелямиДРдифракционной решётки: D_л ≈ fm/h.(10.196)

Угловая ширина главного дифракционного максимума нулевого порядка плоской монохроматической световой волны

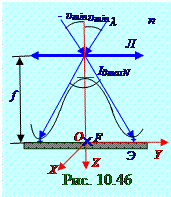
От ДРдифракционной решётки(рис. 10.37) вторичнаясферическая волна, имеющая световую волну с длиной λ, гдеλ = λ₀ /n–длинасветовой волны в однородной изотропной среде с

n показателем преломления, поэтому оптическаяλ = λ₀ /nдлинаэтой световой волны совпадает с геометрическими размерами на рис. 10.35, распространяется от каждой из N щелей, находящихся на h расстояниидруг от друга, под υ_min углом к главной оптическойOZ осиЛ линзы.

Если υ_min ≈ ±λ/Nh, то с учётом малости υ_min угла к главной оптическойOZ оси Л линзы при дифракции имеет место следующее соотношение: sin ± υ_min = sin ± λ/Nh ≈ ± λ/Nh.(10.197) Подставляем (10.197)в (10.158) и получаем следующую I_υminNинтенсивность световойволны при распространении от ДРдифракционной решётки вторичнойсферической волна под υ_min ≈ ±λ/Nh углом к главной оптическойOZ осиЛ линзы:

I_υminN ≈ I_d[sin²(πd/Nh)]/(πd/Nh)²][sin²π]/[sin²(π/N)] = 0. (10.198)

Согласно (10.198)световаяволна (рис. 10.46)λ длиной, которая распространяется от каждой из N щелей, находящихся на h расстояниидруг от друга, под υ_min ≈ ±λ/Nh угломк главной оптической

Разрешающая способность дифракционной решёткипо критерию Релея

От ДРдифракционной решётки(рис. 10.37) вторичнаясферическая волна, имеющая световые волны с длинами λ и λ+δλ, гдеλ = λ₀ /n–длинасветовой волны в однородной изотропной среде с n показателем преломления, поэтому оптическаяλ = λ₀ /nдлинаэтой световой волны совпадает с геометрическими размерами на рис. 10.2.0.47, распространяется от каждой из N щелей, находящихся на h расстояниидруг от друга, под υ_imaxλ и υ_imaxλ+δλ углами к главной оптическойOZ оси

Л линзы.

Каждая световаяволна с длинами λ и λ+δλ образует на Э экране главные дифракционные максимумыc i - ыми значениями, под которыми производят наблюдение главных дифракционных максимумовm - ого порядка, имеющее одинаковое значение для этих λ и λ+δλ длин световых волн.

Вследствие малости υ_imaxλ и υ_imaxλ+δλ углов, под которыми наблюдаются на Э экране главные дифракционные максимумы m - ого порядка, справедливы следующие соотношения:

sinυ_imaxλ ≈ υ_imaxλ и sin υ _maxλ+δλ ≈ υ_maxλ+δλ. (10.200) По критериюРелеяглавные дифракционные максимумы m - ого порядка будут различимы, если центрэтого главного дифракционного максимума m - ого порядка отсветовойволны с

λ длиной, имеющий υ_imaxλ угол к главной оптическойOZ оси Л линзы, будет отстоять от главного дифракционного максимуматого жеm - ого порядка световойволны с λ+δλ длиной на угол,не

одинаковое значение для этих λ и λ+δλ длин световых волн.

Для υ_imax, υ_imaxλ+δλ углов согласно (10.161) выполняются следующие условия:

hsinυ_imax = ± mλ; hsinυ_imaxλ+δλ = ± m(λ+δλ). (10.202) С учётом малости υ_maxλ и υ_maxλ+δλ углов, под которыми наблюдаются на Э экране главные дифракционные максимумы m - ого порядка, т.е. при условии выполнения условия (10.202), положительныезначения этих υ_imaxλ и υ_imaxλ+δλ углов определятся из (10.202) выражения: hsinυ_imaxλ = mλ ↔ υ_imaxλ ≈ mλ/h; hsinυ_imaxλ+δλ = m(λ+δλ) ↔ υ_imaxλ+δλ ≈ m(λ+δλ)/h. (10.203) Подставляем (10.203) в (10.201) и для определения минимальногоδλотклоненияот λ длины световойволны, при котором главные дифракционные максимумыm - ых порядков световыхволн с λ и λ+δλ длинами будут по критериюРелеяразличимы, заменяем неравенствов (10.201) равенствоми получаем следующее выражение Rразрешающей способности дифракционной решётки: [m(λ+δλ)/h] - [mλ/h] = λ/Nh ↔ λ/δλ = mN ↔ δλ = λ/mN ↔ δλ = λ/R, (10.204) где δλ - минимальная разность двухдлин волн или двух спектральных линий, при которой после их прохождения дифракционной решёткиобразуются различимые по критериюРелеяглавные дифракционные максимумы; R = mN - разрешающая способность дифракционной решётки.