Исследование характеристик прозрачной и отражательной дифракционных решеток

Цель работы – научиться собирать и юстировать установку с плоской дифракционной решеткой, рассчитывать по измеренным данным основные характеристики дифракционных решеток, оценивать разницу в спектрах амплитудной и фазовой решеток.

Дифракционные решетки широко применяются в спектральных приборах в качестве диспергирующих элементов, т.е. для разложения излучения в спектр. Дифракционные решетки – это оптические устройства, обеспечивающие периодическую модуляцию падающей световой волны по амплитуде или по фазе. Поэтому различают соответственно амплитудные и фазовые дифракционные решетки.

Дифракционная решетка представляет собой оптическую поверхность, на которую нанесены штрихи, определенным образом разбивающие фронт падающей волны на когерентные пучки. Интерференция этих когерентных пучков света определяет результирующее распределение энергии излучения в пространстве и спектроскопические характеристики решетки.

Наиболее широко используемый метод нанесения штрихов – нарезание штрихов алмазным резцом с помощью специальных делительных машин. Они позволяют наносить штрихи через строго одинаковые промежутки, которые называются периодом дифракционной решетки.

В последнее время разработана новая технология нанесения штрихов путем регистрации на специальных светочувствительных материалах интерференционной картины от двух когерентных пучков света. Это так называемые голографические дифракционные решетки.

Существуют прозрачные и отражательные дифракционные решетки. У прозрачных решеток результирующая интерференционная картина образуется в проходящем свете, у отражательных – в отраженном свете.

Дифракционные решетки называют плоскими, если штрихи решетки нанесены на плоскую поверхность, и вогнутыми, если штрихи нанесены на вогнутую сферическую или асферическую поверхности. Решетки с переменным периодом и штрихами непрямолинейной формы и вогнутые решетки обладают фокусирующим действием.

Изготовление дифракционных решеток высокого качества представляет значительные трудности, и они очень дорогие. Поэтому в технике применяют копии таких решеток, которые называются репликами. С этой целью с оригинальной решетки снимают слепок из полиэфирной смолы – матрицу. Повторные слепки с матрицы – реплики, которые покрываются отражающим слоем, и являютcя техническими дифракционными решетками. В современных спектральных приборах используются, главным образом, отражательные фазовые дифракционные решетки и реплики.

Действие дифракционной решетки можно понять, если рассмотреть интерференцию отдельных плоских волн, испытавших дифракцию на щелях решетки. В результате интерференции лучей, исходящих из соседних щелей, будут наблюдаться максимумы, когда разность хода лучей D₂ - D₁ будет равна целому числу волн (рис. 1).

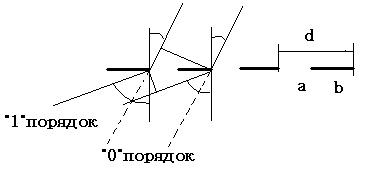
Рис. 1. Дифракция на прозрачной решетке

Вычисляя, исходя из обозначений рис. 1, эту разность хода, получим известную формулу

d (siny - sinj) = ml, (1)

где d = a + b – постоянная решетки, y, j – соответственно углы падения и дифракции, m – целое число (порядок спектра), l длина волны. Эта формула называется основным уравнением дифракционной решетки.

При расчетах по (1) необходимо пользоваться правилом знаков при углах j и y. Если углы падения j и дифракции y располагаются по разные стороны от нормали к поверхности решетки, то они берутся с одинаковыми знаками (рис. 1, y>0, j>0), если по одну сторону от нормали, то с разными.

Решетка может давать большое число дифракционных максимумов с данной длиной волны l, соответствующих разным порядкам m и углам дифракции j (до ± 90⁰). При m = 0 получаем дифракционный максимум нулевого порядка, для которого siny = sin(j) независимо от длины волны. Однако реально наблюдается ограниченное число ярких максимумов, число которых определяется шириной дифракционной картины при дифракции света на щели шириной а, а также постоянной решетки d (рис. 1).

Максимальное значение m ограничивается условием |siny + sinj| £ 2. Из (1) получаем ml £ 2d, и, следовательно, m_max = 2d/l. Решетки, как правило, характеризуются числом N₁ штрихов на мм, причем N₁=1/d.

Cпособность дифракционной решетки разводить (диспергировать) излучения разных длин волн на различные углы характеризуется угловой дисперсией D_j . Она получается дифференцированием (1) по l. Это дает

D_j = dj/dl = m / d cosj = mN₁/cosj.

Дисперсия возрастает с увеличением m и N₁. Поскольку cosj мало меняется с ростом угла дифракции при небольших j, то

D_j » const и спектр дифракционной решетки является практически равномерным. Основное уравнение (1) решетки показывает, что одни и те же углы дифракции будут наблюдаться для всей совокупности длин волн l_i, удовлетворяющих соотношению d(siny + sinj) = m_il_i. Таким образом, если для наибольшей наблюдаемой длины волны l спектр первого порядка расположен под углом j к нормали, то под этим же углом будет наблюдаться излучение с длиной волны l/2 в спектре второго порядка, l/3 – в спектре третьего порядка и т.д. Это явление называется переналожением порядков в спектре дифракционной решетки. Разделение спектров в этом случае осуществляется достаточно просто путем использования абсорбционных светофильтров, которые выбираются таким образом, чтобы они поглощали излучение высоких порядков спектров. Область спектра свободную от переналожения порядков (область свободной дисперсии) можно рассчитать по формуле D^¢l = l/m+1. Поэтому для работы в достаточно широком диапазоне D^¢l = l₂ - l₁ необходимо работать при m = 1.

Дифракционную решетку, как и любой спектральный прибор, можно охарактеризовать некоторой теоретической разрешающей способностью. Если исходить из критерия разрешения по Релею, то угловое расстояние между пучками лучей с длинами волн l₁ и l₂, находящимися на пределе разрешения, будет dj = l/D^¢. При этом расстояние между ними, выраженное в длинах волн, равно dl = l₂ - l₁. С другой стороны, это расстояние dl можно рассчитать через угловую дисперсию решетки dl = dj/D_j = l/D^¢D_j. Тогда для теоретической разрешающей способности R_T получаем следующее выражение

R_T = l/dl = D^¢D_j,

где D^{¢ –} сечение пучка лучей в направлении угла дифракции j, равное Ndcosj.

Окончательно для теоретической разрешающей способности решетки получаем

R_T = D^¢ D_j = N d m cosj / d cosj = m N.

Она зависит от порядка спектра m и общего числа штрихов N решетки. Подставляя в выражение для R_T максимальное значение числа порядков, возможных для данной решетки, получим максимальную теоретическую способность дифракционной решетки R_Тmax = 2Nd/l = 2L/l, где L – длина нарезанной части решетки. R_T современных решеток в зависимости от размеров и числа штр/мм может достигать нескольких сотен тысяч. Некоторые технические параметры дифракционных решеток приведены в [2].

Плоские амплитудные решетки используются главным образом для измерительных целей (измерение перемещений).

В спектральных приборах применяются профилированные фазовые отражательные решетки. Они представляют собой регулярную последовательность зеркальных канавок треугольного не симметричного профиля (рис. 2). Рабочая зеркальная грань более широкая, чем не рабочая. Световая волна дифрагирует на рабочих гранях и в отраженном свете получается пространственное распределение интенсивности. Дифракционный максимум от каждой зеркальной грани расположен в направлении зеркального отражения луча. Поэтому в этом направлении будет максимум энергии J_max , отраженной от решетки. Его положение в пространстве будет зависеть от угла i наклона рабочей зеркальной грани, а также от длины волны l .

Изменяя угол i наклона грани, можно смещать по спектру (в пределах как одного порядка, так и по разным порядкам) положение максимума энергии. Такие решетки с концентрацией энергии в определенный порядок спектра называются эшелеттами [1,2]. Длина волны l_Jmax для заданного i можно определить по формуле

l_Jmax = 2sin(i) cos (0.5q) / mN₁,

где q = |y - j | - угол отклонения лучей дифракционной решеткой.

Область длин волн вблизи l_Jmax называют областью высокой концентрации энергии в данном порядке спектра, а угол i – углом блеска эшелетта. В случае автоколлимационной схемы y = j = i и q = 0. Тогда

l_Jmax = 2sin(i) / mN₁ = 2d sin i / m .

Если сравнивать интенсивности спектров амплитудной и профилированной фазовой решеток , то окажется , что в первом случае имеет место яркий нулевой максимум и интенсивности одноименных спектров одинаковы и их яркость уменьшается с увеличением порядка спектра, а во втором – имеет место яркий спектр определенного порядка , яркость остальных значительно меньше. На рис.3 представлены кривые распределения энергии для различных порядков профилированной фазовой отражательной дифракционной решетки.

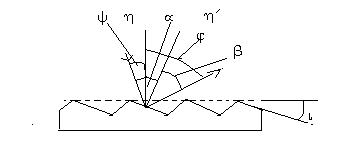
Рис. 2. Дифракция на фазовой решетке

y,j – углы падения и дифракции; a,b – углы падения и дифракции для рабочей зеркальной грани; i – угол наклона рабочей грани (угол блеска); h,h´ – нормали к решетке и рабочей грани соответственно.

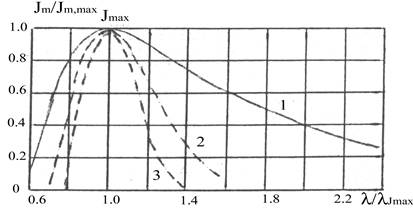
Рис. 3. Распределение энергии по порядкам решетки

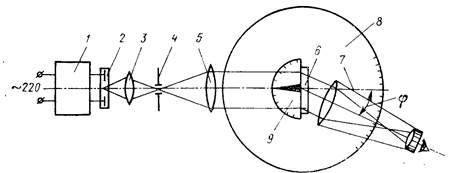
Рис. 4. Схема установки для исследования дифракционных решеток

1 – блок питания источника; 2 – источник линейчатого спектра; 3 – конденсор (f^¢=110 мм); 4 – спектральная щель; 5 – коллиматорный объектив (f^¢=170 мм); 6 – дифракционная решетка; 7 – зрительная труба; 8 – лимб для определения угла поворота зрительной трубы; 9 – полулимб для измерения углового положения решетки в пучке лучей.

Задание

1. Собрать и отъюстировать установку по схеме рис. 4.

2. Наблюдать спектры амплитудной и фазовой дифракционных решеток. Объяснить в чем их различие.

3. Для прозрачной амплитудной решетки:

– измерить зависимость sinj = f(l), где j - угол дифракции для излучения с длиной волны l, и определить по ней период d дифракционной решетки. Экспериментально найденное значение периода сравнить с паспортным;

– рассчитать угловую дисперсию D_j решетки и линейную дисперсию D_L установки в первом и втором порядках спектра.

4. Для фазовой отражательной решетки:

– экспериментально проверить основное уравнение дифракционной решетки;

– вычислить по заданному углу профиля штриха длину волны l_max, соответствующую максимуму в распределении энергии в спектре первого порядка дифракционной решетки, и построить график относительного распределения энергии J_{отн =} f(l) в спектре третьего порядка решетки для случая автоколлимационной схемы (y = j).