Вектор индукции магнитного поля 3 страница
v\\ составляющей вектора v скорости,параллельным вектору B индукции внешнего однородного магнитного поля,преодолеет по OX оси неподвижной OXYZ системы координат запромежуток
Δt времени: l = Δtv\\ = v\\T = v(2πm/q+B)cosα,(7.43) где Δt = T - промежутокt времени, равный (7.42) T периоду полного оборота q+ положительного заряда m массыпо окружности R радиуса с центром, лежащим на OY оси этой неподвижной
OXYZ системы координат.
Выражения (7.42), (7.43)справедливы не только для расчёта параметров движения заряженной частицы с q+ положительным зарядом, но и для движения заряженной частицы с q- отрицательнымзарядом в однородном магнитном поле. В случае расчёта параметров движения заряженной частицы с
q- отрицательнымзарядом в однородном магнитном поле в выражениях (7.42), (7.43) следует использовать модуль |q-| этого q- отрицательного заряда.
Выражения (7.42), (7.43) справедливы для расчёта параметров движения в однородном магнитном поле заряженной частицы с q+ положительным зарядомили q- отрицательным зарядом согласно параграфу "Инвариантность уравнений механики относительно преобразований Галилея" из раздела 3.0 "Релятивистская механика" при нерелятивистскомзначении v модуля вектора v скорости этой заряженной частицы с m массой.
Движение заряженной релятивистской частицы в однородном магнитном поле
При релятивистскомзначении модуля v вектора v скорости заряженной частицы m массой согласно параграфу "Элементы релятивистской динамики: основное уравнение релятивистской динамики, кинетическая энергия релятивистской частицы" из раздела 3.0 "Релятивистская механика" для расчёта параметров движения в однородном магнитном поле этой заряженной частицы с q+ положительным зарядомили q- отрицательным зарядом применяется (3.47) из раздела 3.0 "Релятивистская механика" основное уравнение релятивистской динамики, имеющее следующий вид: d[mv/(1 - (v2/c2)1/2]/dt = F, (7.44)
где [1-(v2/c2)]1/2- не зависящий от t времени (3.32) из раздела 3.0 "Релятивистская механика" релятивистский множитель; F - релятивистскийвектор силы, действующий на движущуюся заряженную частицу с m массой.
С использованием правил дифференцирования от дроби и функции от функции первая d[mv/(1 - (v2/c2)1/2]/dt производная в (7.44) выражении имеет следующий вид: m[(dv/dt)/(1 - (v2/c2)1/2] + m{(v/c2) [v(dv/dt)]/(1 - (v2/c2)3/2} = F,(7.45)
где при дифференцировании стоящую в (7.45) знаменателе под знаком корня величину квадрата модуля v2 вектора v скорости заряженной релятивистскойчастицы m массой нужно представить в виде квадрата вектора v2 скорости этой заряженной частицы.
В (7.45) dv/dt представляет собой вектор a ускорения релятивистскойчастицы mмассой, поэтому с учётом dv/dt = a, а также после умножения левой и правой частей выражения (8.90) на вектор v скорости заряженной релятивистской частицы это выражение (8.90) принимает следующий вид:
m[(va)/(1 - (v2/c2)1/2] + m[(v2/c2)(va)/(1 - (v2/c2)3/2] = vF,(7.46)
Решение (7.46) уравнения относительно (va) скалярного произведения векторов соответственно скоростии ускорения релятивистскойчастицы mмассойимеет следующий вид:
va = vF/ m{[1/(1 - (v2/c2)1/2] + [(v2/c2)/(1 - (v2/c2)3/2]}. (7.47)
С учётом v(dv/dt) =vaравенства подставляем (va) скалярное произведение (7.47) векторов соответственно скоростии ускорения релятивистскойчастицы mмассойв (7.46), вследствие чего после тождественных преобразований выражение a = dv/dt ускорения релятивистскойчастицы mмассойиз (7.45) принимает следующий вид: m[a/(1 - (v2/c2)1/2] + m(v/c2)(vF)/ (1 - (v2/c2)3/2m{[1/(1 - - (v2/c2)1/2] + [(v2/c2)/(1 - (v2/c2)3/2]} = F ↔ a = (1 - (v2/c2)1/2[(F/m) – (vF/mc2)v]. (7.48)В случае перпендикулярности вектора (рис. 7.10) Fm силы Лоренца вектору v скорости заряженной релятивистской частицы m массой, вследствие чего (vF) скалярное произведение будет равно нулю, т.е. vF = 0, и aускорение релятивистскойчастицы mмассойв (8.94) принимает следующий вид: a = (1 - (v2/c2)1/2F/m, (7.49)
где векторы aускорения релятивистскойчастицы mмассой и Fmсилы Лоренца коллинеарныи вследствие положительного значения (1 - (v2/c2)1/2/m направлены в одну сторону. Поэтому вектор aускорения релятивистскойчастицы mмассой направлен к центру окружности R радиуса, по которой вращается с v модулем вектора v скорости релятивистская заряженная частицы, и выражение (7.49) для модулей векторов принимает следующий вид: v2/R = (1 - (v2/c2)1/2qvB/m, (7.50) где q = |q-| = q+ модуль заряда релятивистской частицы; v2/R - модуль вектора a центростремительного ускорения релятивистскойчастицы; qvB -модуль вектора Fm силы Лоренца, направленного к центру окружности R радиусом, по которой с vмодулем вектораv скорости двигается заряженная релятивистская частица; B - модуль вектора B индукции магнитного поля, направленного
(рис. 7.11) перпендикулярно плоскости, образованной векторами v скорости релятивистской заряженной частицы и Fm силы Лоренца.
По аналогии с (7.42) из (7.50) имеем следующие выражения:
R = (m/qB)v/[1-(v2/c2)]1/2 ↔ T = 2πR/v ↔ T = 2πm/qB(1-(v2/c2)1/2,(7.51)
где T -период полного оборота по окружности R радиуса с центром, лежащим (рис. 7.11) на OY оси неподвижной OXYZ системы координат, заряженной релятивистской частицы m массой с
q+ положительным зарядомили q- отрицательнымзарядом, имеющем модуль q заряда, согласно (7.51) зависит от модуля vвектораv скорости движения этой заряженной частицы.
Отклонение от прямолинейной траектории движущейся заряженной нерелятивистскойчастицы однородным электрическим полем
|
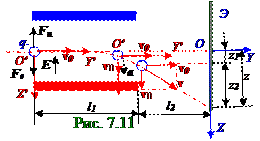
Fe -направленный вниз к положительнозаряженнойпластине вектор силы, действующий на отрицательный q- заряд cо стороны внешнего однородного электрического поляс вектором
E напряжённости.
Проекция на O′Z′ ось (1.46) из раздела 1.0 "Физические основы механики"второго законаНьютона без учёта силы тяжести отрицательного q- заряда m массыв неинерциальной подвижнойO′Y′Z′ системе координат, поскольку этаподвижнаяO′Y′Z′ система координат двигается (рис. 7.11) вместе с отрицательным q- зарядом с вектором aускорения по направлениюOZ оси неподвижной
OYZ системы координат, а по направлениюOY оси неподвижной OYZ системы координат двигается равномерно с вектором v0 скорости,имеет следующий вид:
O′Z′: 0 = FиZ′ + FeZ′ = - ma + qE ↔ a = (q/m)E, (7.53) где a –модульвектора aускорения подвижнойO′X′Y′ системы координат, которая двигается вместе с отрицательным q- зарядом по направлениюOZ оси неподвижной OYZ системы координат; FиZ′ = - ma - отрицательноезначениепроекции на O′Z′ ось вектора Fиинерциальнойсилы, поскольку этот вектор Fиинерциальнойсилы направлен вотрицательную сторону O′Z′ оси подвижнойO′Y′Z′ системы координат; FeZ′ = qE - положительноезначениепроекции на O′Z′ ось (8.83) вектора Fe силы, поскольку этот вектор Fe силы направлен в положительную сторону O′Z′ оси подвижнойO′Y′Z′ системы координат; q=|q-| -модуль отрицательного заряда.
Кинематический (1.13) из раздела 1.0 "Физические основы механики"расчёт (рис. 7.11) движенияотрицательного q- зарядас учётом его равноускоренногодвижения с вектором aускорения по направлениюосиOZ неподвижной OYZ системы координат на l1 длине заряженныхпластин, а также с учётом равномерногодвижения с вектором vскоростив неподвижной OYZ системе координат на l2 длине от окончания заряженных пластин до Э экрана, приводит к следующему выражению z смещения отрицательного q- заряда относительно начала O в неподвижной OYZ системе координат: z = (q/m)E(l1/v02 )[(l1/2)+ l2], (7.54)
где v0 -модуль вектора v0 начальнойскорости движенияотрицательного q- заряда по направлениюосиOY неподвижной OYZ системы координат.
Отклонение от прямолинейной траектории движущейся заряженной нерелятивистскойчастицы однородным магнитным полем
На (рис. 7.12) заряженную нерелятивистскуючастицу,имеющуюотрицательный q- заряд и движущуюся с вектором v0 скоростив вакууме, перпендикулярным вектору B индукции магнитного поля, действует (7.38) векторFm силы Лоренца.
Проекция на O′Z′ ось (1.46) из раздела 1.0 "Физические основы механики"второго законаНьютона без учёта силы тяжести отрицательного q- заряда m массыв неинерциальной подвижнойO′X′Y′ системе координат, поскольку этаподвижнаяO′X′Y′ система координат двигается (рис. 7.12) вместе с отрицательным q- зарядом с (1.16) из раздела 1.0 "Физические основы
механики"свектором an нормальногоускорения по окружностиR радиусом, имеет следующий вид: O′Z′: 0 = FиZ′ + FmZ′ = - man + qv0B ↔ 0 = - m(v02/R) + qv0B ↔ R = mv0/qB, (7.55)
где an= v02/R –модульвектора an нормального ускорения подвижнойO′Y′Z′ системы координат, которая двигается вместе сотрицательным q- зарядом по окружностиR радиусом;
FиZ′ = - man - отрицательноезначениепроекции на O′Z′ ось вектора Fиинерциальнойсилы, поскольку этот вектор Fи инерциальнойсилы направлен вотрицательную сторону O′Z′ оси подвижнойO′Y′Z′ системы координат; FmZ′ = qv0B - положительноезначениепроекции на O′Z′ ось (8.84) вектораFm силы Лоренца, поскольку этот вектор Fq силы Лоренца направлен в положительную сторону O′Z′ оси подвижнойO′Y′Z′ системы координат; q=|q-| -модуль отрицательного заряда.
|
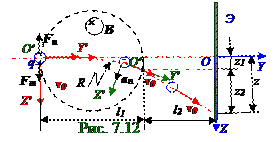
приближенно можно считать равномерным с вектором v0 скорости.
С учётом перечисленных допущений (рис. 7.12) выражение z смещенияотрицательного
q- заряда относительно O начала в неподвижной OYZ системе координат аналогично (8.100) выражению имеет следующий вид: z = (q/m)(B/v0 )l1[(l1/2)+ l2]. (7.56)
Эффект Холла
Эффектом американского физика Эдвина Герберта Холла(1855 - 1938) называется возникновение поперечного электрического поля в проводнике или полупроводникес током при помещении его в магнитное поле.
Согласно (рис.6.1) из раздела 6.0 "Электрический ток"за направление тока принимается направление, в котором перемещаются q+ положительныеносители электрического тока, поэтому носители электрического тока (рис. 7.13, а), которыми в проводнике являются электроны, приплотности электрическоготока в направлении вектора j плотности электрическоготока по OY оси двигаютсяупорядоченно c векторомui скорости по направлению, противоположном OY оси.
|
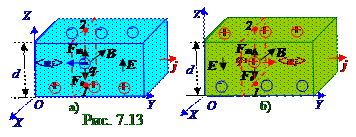
векторFm силы Лоренца. При применении правила "левой руки" для случая (рис. 7.13, а) вытянутые четыре пальца левой руки нужно направлять противоположно среднему значению вектора <ui> скоростидвиженияq- отрицательных зарядов. В этом случае траектории движения q- отрицательных зарядов отклоняются от направления по OY оси и приобретают вследствие воздействия вектораFm силы Лоренцасоставляющий векторскорости, направленный по OZ оси. Поэтому на верхней грани параллелепипеда возникает избыток q- отрицательныхзарядов и между нижней и верхней гранями параллелепипеда возникает электрическое поле с вектором E напряженностиэтого электрического поля. Возникшее электрическое поле между нижней и верхней гранями параллелепипеда с вектором E напряженностиэтого электрического поля вызывает появление (8.82) вектора Fe силы, имеющий следующий вид: Fe= q-E, (7.57)
где вектор Fe силы (рис.7.13, а) имеет направление, противоположное вектору
E напряженностиэлектрического поля, вследствие отрицательногочисленного значения
q- отрицательныхзарядов.
Накопление q- отрицательныхзарядов на верхней грани параллелепипеда прекратится и возвращение их траектории движения к прямой линии по OY оси произойдёт тогда, когда сила Лоренцабудет уравновешенасилойэлектрического поля, т.е. когда будет выполняться следующее соотношение: Fe + Fm = 0 ↔ q+ [<ui >, B] = - q-E ↔ [<ui >, B] = E, (7.58) где векторFm силы Лоренца(7.38) представлен для положительныхносителей электрического тока и среднего значения вектора <ui > скорости положительныхносителей электрического тока, совпадающего по направлению с вектором j плотности электрическоготока по OY оси.
Вектор среднего значения <ui > скорости положительныхносителей электрического тока, который направлен в противоположную сторону (рис. 7.13, а) среднему значению вектора
<ui > скоростиq- отрицательныхзарядов и совпадает по направлению с вектором j плотности электрическоготока по OY оси, перпендикуляренвектору B индукции магнитного поля, поэтому (7.58) для модулей имеет следующий вид: uiB = E.(7.59)
Подставляем (6.7) из раздела 6.0 "Электрический ток"модуль j = q+ n+u+ вектора j плотности электрическоготока в (8.103) и получим следующее выражение: jB/ q+ n+ = E,(7.60)
где q+, n+, u+ -соответственно величина заряда, концентрация и модуль среднего значения векторов
<ui> скорости движенияположительных носителей электрического тока, которые равны по своим значениям (рис. 7.13, а) модулюq- отрицательныхзарядов, n- концентрации q- отрицательныхзарядов, модулю ui среднего значения векторов <ui> скорости движенияq- отрицательныхзарядов.
Разностьφ1 - φ2 потенциалов (рис. 7.13, а) между нижней и верхней гранями параллелепипеда согласно (5.117) из раздела 5.2 "Электростатическое поле в диэлектрике.Электрическое поле заряженных проводников. Энергия электростатического поля " с учётом постоянного значения проекции EZ на OZ ось вектора E напряженностиэлектрического поля между этими нижней и верхней гранями параллелепипеда с учётом (8.105) имеет следующий вид:
dd φ1 - φ2 = ∫EZdz = EZ∫dz = jBd/q+ n+, (7.61)
0 0
где d - расстояние (рис. 7.13, а) между нижней и верхней гранями параллелепипеда.
По величине разностиφ1 - φ2 потенциалов (рис. 7.13, а) между нижней и верхней гранями параллелепипеда определяют, например, n+ концентрацию положительныхносителей электрического тока, которая по своему значению равна n- концентрации q- отрицательныхзарядов в случае наблюдения эффекта Холла у металлов. По знаку разностиφ1 - φ2 потенциаловмежду нижней и верхней гранями параллелепипеда определяют знак носителей электрического тока. В случае положительных носителей электрического тока, например, у полупроводников,на верхней грани параллелепипеда(рис. 7.13, б) возникает избыток положительных q+ зарядов, поэтому φ2 потенциал верхней грани параллелепипеда будет больше φ1 потенциала нижней грани параллелепипеда иразностьφ1 - φ2 потенциаловбудет меньше нуля.
Определение удельного заряда нерелятивистскогоэлектрона
Удельный q/m заряд электронабыл впервые измерен английским физиком Джозефом Джоном Томсоном (1856 - 1940) в 1897 г.
|
Под влиянием магнитного поля с (рис. 7.14) вектором B индукции этого магнитного поля нерелятивистские электроны, вылетающие из К катода и ускоренные электрическим полем А анода в электронно - лучевойтрубке, отклоняются на Э экране на величину z смещения относительно O начала в неподвижной OYZ системе координат под влиянием (7.38) вектораFm силы Лоренца. Это
z смещение относительно O начала в неподвижной OYZ системе координат определяется (7.56) следующим выражением: z = (q/m)B(l1/v0 )[(l1/2)+ l2] = (q/m)(B/v0 )K ↔ v0 = K(q/m)(B/z), (7.62) где K = l1[(l1/2)+ l2] - геометрический (рис. 7.14) параметр электронно-лучевойтрубки; m - масса электрона; v0 - модуль вектора v0 скорости электрона, перпендикулярного вектору B индукции внешнего магнитного поля; q= |q-| -модуль заряда электрона.
После измерения x смещения электронов относительно O начала в неподвижной OYZ системе координат под влиянием (7.38) вектораFm силы Лоренца наотклоняющие Пл пластины подаётся постоянное напряжение, в результате чего между этими отклоняющими Пл пластинами создаётся однородное(5.25) из раздела 5.1 «Электрическое поле системы неподвижных зарядов в вакууме. Теорема Гаусса для электростатического поля. Работа и потенциал электростатического поля» электрическое поле с вектором
Дата добавления: 2016-02-14; просмотров: 820;