Статистическое описание равновесных состояний термодинамических систем: одно -, дву – и трехмерные функции распределения 3 страница

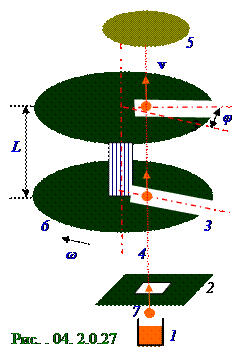
Время Δt пролёта атомов7 металла, летящих с v_i модулем вектораv_i скорости от 3 прорези нижнего диска до 3 прорезиверхнегодиска, которые расположены на L расстояниидруг от друга, имеет следующее значение: Δt = L/v. (4.276)

Статистическое описание равновесного состояния термодинамических систем с помощью фазового пространства (каноническое распределение Гиббса)

Система N одинаковых взаимодействующихмежду собой частиц в классическойдинамике описывается (1.1) из раздела 01.0.0 «Физические основы механики» r_i радиусом - вектором

i - ойчастицы, соединяющим O начало координат с этой частицей, и (1.41) из раздела 01.0 «Физические основы механики»вектором p_i её импульса.

Полная совокупность r₁, r₂,.. , r_i, .. , r_N радиусов - векторови векторов p₁, p₂,.. , p_i, .. , p_N импульсов всех частиц, входящих в систему, описывает состояние этой системы в целом.

Взаимодействиемежду собой не имеющих внутреннейструктурычастиц в макроскопическойсистеме, например, взаимодействиемежду собой молекул реального газа в параграфе "Эффект Джоуля – Томсона" из раздела 04. 1.0 "Физическая термодинамика"описываютпотенциальнымифункциями следующего вида: W_pij= W_pij (r_i, r_j), (4.278) где W_pij- потенциальная в параграфе "Консервативные силы. Работа в потенциальном поле" из раздела 01.0.0 «Физические основы механики»и энергия (5.137) из раздела 05.2.0 "Электростатическое поле в диэлектрике. Электрическое поле заряженных проводников. Энергия электростатического поля" взаимодействия W_вз между i - ой и j - ойчастицами, входящими в эту макроскопическуюсистему, причём j ≠ i.

Полная энергия системы N одинаковых взаимодействующихмежду собой частиц описывается H функцией Гамильтона, которая равна (1.89) из раздела 01.0.0 «Физические основы механики»

N N

W_k(p_i) = ∑W_ki = ∑p_i²/2m суммекинетическихэнергий этих N частиц,где p_i - вектор импульса

i = 1 i = 1

i - ойчастицы, и сумме (1.94) из раздела 01.0.0 «Физические основы механики»

N N

W_p(r_i, r_j)= (1/2)∑ ∑ W_p(r_i, r_j) потенциальных энергий взаимодействия между i - ой и j - ой

i = 1 j = 1

частицами, причём j ≠ i, вследствие чего для определения H(r_i,p_i) функции Гамильтона имеет место N N N

следующее выражение: H(r_i,p_i) = ∑p_i²/2m + (1/2)∑ ∑ W_p(r_i, r_j), (4.279)

i = 1 i = 1 j = 1

j ≠ i

где W_pij (r_i, r_j) - потенциальная энергия взаимодействия между i - ой и j - ойчастицами, имеющих соответственно (рис.1.1) из раздела 01.0.0 «Физические основы механики» r_i и r_j радиусы - векторы; коэффициент 1/2 учитывает равенство потенциальных энергий взаимодействиймежду частицамипри перестановке номеров частиц, например, W_p(r₁, r₂) = W_p(r₂, r₁), поэтому при двойном суммировании в (4.239) потенциальная энергия взаимодействия между i - ой и j - ойчастицамиприсутствуетдваждыи для получения истинного значения потенциальной энергии взаимодействия перед двойной суммой введён 1/2 коэффициент.

МакроскопическоесостояниеN одинаковых взаимодействующихмежду собой частиц задаётсясовокупностью r₁, r₂,.. , r_i, .. , r_N радиусов - векторовивекторов p₁, p₂,.. , p_i, .. , p_N импульсов всех Nчастиц. Радиус - вектор r_i, соединяющий O начало координат с i - ой частицей, имеет

(рис.1.1) из раздела 01.0.0 «Физические основы механики» вдекартовой системе координат

x_i, y_i и z_i координаты концаэтого r_i радиуса - вектора, а V_r представляет собой объём, построенный на координатных OX, OY и OZ осях, в котором находятся все Nчастиц. В прямоугольной декартовой (рис.1.1) из раздела 01.0.0 «Физические основы механики» системе координат, по координатным Op_X, Op_Y и Op_Z осям которой откладываются (рис. 04. 2.0.25) проекции p_iX, p_iY и p_iZ вектора p_i импульса

i - ойчастицы, представляет собой p - пространство или пространство импульсов, а V_p представляет собой объём, построенный на координатных Op_X, Op_Y и Op_Z осях, в котором находятся все проекции p_iX, p_iY и p_iZ векторов p_i импульсов Nчастиц.

Произведение V_rV_p = V_rp представляет собой шестимерный объём координатного и импульсного пространства, в котором находятся x_i, y_i, z_i координаты концов r_i радиусов - векторови проекции p_iX, p_iY, p_iZ вектора p_i импульсов всех Nодинаковых взаимодействующихмежду собой частиц.

Замкнутая термодинамическая система с заданным Nчислом одинаковых взаимодействующихмежду собой частиц, характеристики которой находятся в известном

V_rp шестимерном объёме координатного и импульсного пространстваи находящейся в тепловомконтакте с термостатом, имеющем Tтемпературу, т.е. имеющей постояннуюTтемпературу, называется каноническим ансамблем Гиббса. Для этого ансамбля введено каноническое распределение Гиббса, имеющее следующий вид: f(r_i, p_i) = (1/θ)exp-[H(r_i,p_i)/kT]. (4.280)

Постоянную θ определяют из следующего условия нормировки (4.280) выражения:

1 = (1/θ)∫ exp-[H(r_i,p_i)/kT]dV_rp ↔ θ = ∫ exp-[H(r_i,p_i)/kT]dV_rp, (4.281)

V_rp V_rp

N

где dV_rp = ∏dx_idy_idz_idp_iXdp_iYdp_iZ - элементарный объём шестимерного координатного и импульсного

i = 1

пространства, который представляет собой произведение элементарных приращений x_i, y_i, z_i координат и проекций p_iX, p_iY, p_iZ вектора p_i импульсов всех Nодинаковых взаимодействующихмежду собой частиц, т.е представляет собой 6N - мерную независимую интегрирования.

С помощью (4.280) канонического распределения Гиббса можно определить наблюдаемые макроскопическиепараметры любой термодинамической системы, находящихся в равновесномсостоянии и имеющих неизменное число Nодинаковых взаимодействующихмежду собой частиц.

Однако непосредственное применение (4.280) канонического распределения Гиббса связано с интегрированием6N - мерной f(r_i, p_i) функции распределения, что является затруднительной математической задачей для реальной системы, состоящей из большого количества Nодинаковых взаимодействующихмежду собой частиц.

Поэтому для решения многих прикладных задач используют более простые функции распределения, например, распределение Максвелла – Больцмана, которое может быть получено из (4.280) канонического распределения Гиббса для идеального газа.

Распределение молекул идеального газа по координатам и скоростям (распределение Максвелла – Больцмана)

Согласно (4. 236) распределению Больцманав любом потенциальномполе n концентрациямолекул идеального газа распределяeтся в соответствии с их W_p потенциальнойэнергией в этом поле.

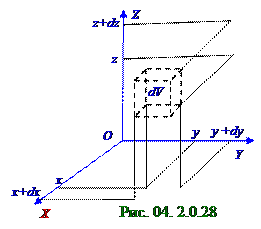
Число (рис. 04. 2.0.28) dN молекул, попадающих в пределы элементарного dV = dxdydz объёма, расположенного в произвольнойточке пространства с координатами x, y и z, где их потенциальнаяэнергия имеет значение W_p, а n = n₀ exp(-W_p/kT) концентрациямолекул в этом месте пространства рассчитывается по (4. 236) выражению, определяется следующим соотношением:

dN = n₀ exp(-W_p/kT)dxdydz. (4.282) В соответствии с (4. 227) вероятность dP(x, y, z) нахождения (рис. 04. 2.0.28) молекул идеального газа в пределах dV = dxdydz объёма, т.е. нахождения координат этих молекул в интервале

x…x + dx, y… y +dy и z… z+dz значений из (4.282) имеет следующий вид:

dP(x, y, z) = dN/N = (n₀/N)exp(-W_p/kT)dxdydz ↔ dP(x, y, z)/dxdydz = f(x, y, z) = (n₀/N)exp(-W_p/kT), (4.283) где N - полное число молекул в данной массе идеального газа; f(x, y, z) = (n₀/N)exp(-W_p/kT)- функция плотностивероятности распределения частиц в потенциальном поле. Она численноравна

следующий вид: f(v_X, v_Y, v_Z) = (m/2πkT)^3/2exp(-mv²/2kT), (4.284) где v_i² = v_iX² + v_iY² + v_iZ²- квадрат модулявектораv_i скоростей молекул идеального газа. Cчитая (4.245)координаты молекул x, y и z по (рис.4.27) осям координат соответственно OX, OY и OZ и (4.246) проекции(рис. 04. 2.0.25) v_iX, v_iY и v_iZ на Ov_X, Ov_Y и Ov_Z оси вектораv_i скоростей молекулстатистически независимыми величинамисовместнаяплотность f(x, y, z, v_X, v_Y, v_Z)вероятностисобытия, которая численноравна вероятности нахождения молекул идеального газа

(рис. 04. 2.0.28) в единичномV объёме пространства с x, y и z координатами, где их потенциальнаяэнергия имеет значение W_p, и одновременного нахождения проекцийv_iX, v_iY и v_iZ на Ov_X, Ov_Y и Ov_Z оси вектораv_i скоростей молекулв (рис. 04. 2.0.25) единичномV объёмескоростей с v_X, v_Y и v_Z координатами по направлению этого вектора v_i скоростей молекул, определяется произведением функции (4.283) f(x, y, z) плотности вероятности и функции (4.284) f(v_X, v_Y, v_Z) плотности вероятности. Поэтому эта совместнаяплотность f(x, y, z,v_X, v_Y, v_Z)вероятности с учётом (4.245), (4.246) имеет следующий вид:

f(x, y, z, v_X, v_Y, v_Z) = f(x, y, z) f(v_X, v_Y, v_Z) = (n₀/N)(m/2πkT)^3/2exp-{[W_p+ (mv²/2)]/kT }. (4.285)

Вероятность dP(x, y, z,v_X, v_Y, v_Z) совместного события- нахождение (рис. 04. 2.0.28) молекул идеального газа в интервале значений координат x…x + dx, y… y + dy и z… z + dz с одновременнымнахождением (рис. 04. 2.0.25) проекцийv_iX, v_iY и v_iZ на Ov_X, Ov_Y и Ov_Z оси вектораv_i скоростей молекул в интервале значений v_X…v_X + dv_X, v_Y…v_Y + dv_Y и v_Z…v_Z + dv_Z по направлению этого вектора v_i скоростей молекул с учётом (4.285) совместнойплотности f(x, y, z,v_X, v_Y, v_Z)вероятности имеет следующий вид: dP(x, y, z, v_X, v_Y, v_Z ) = dN_с/N = f(x, y, z)f(v_X, v_Y, v_Z)dxdydzdv_Xdv_Ydv_Z =

= (n₀/N)(m/2πkT)^3/2 exp{[-(W_p + mv²)/kT} dxdydzdv_Xdv_Ydv_Z ↔

↔ dN_с= n₀(m/2πkT)^3/2exp-{[W_p+ (mv²/2)]/kT }dxdydzdv_Xdv_Ydv_Z,(4.286) где v_i² = v_iX² + v_iY² + v_iZ² - квадрат модуля скоростимолекул идеального газа; N - полное число молекул в данной массе идеального газа; n₀ - концентрация молекул идеального газа при выбранном начальномзначении x₀ , y₀, z₀ координат; dN_с - число (рис. 04. 2.0.28) молекул идеального газа, находящихся в элементарном dV = dxdydz объёме, расположенном в произвольнойточке пространства с x, y и z координатами, с одновременным нахождением (рис. 04. 2.0.25) проекцийv_iX, v_iY и v_iZ на

Ov_X, Ov_Y и Ov_Z оси вектораv_i скоростей молекул в интервале значений v_X…v_X + dv_X, v_Y…v_Y + dv_Y и v_Z…v_Z + dv_Z по направлению этого вектора v_i скоростей молекул.

В выражении (4.286), которое называется распределением Максвелла - Больцмана, функция f(x, y, z, v_X, v_Y, v_Z) = (n₀/N)(m_i/2πkT)^3/2exp -{[W_p+ (mv²/2)]/kT } - этоплотность вероятности, которая численноравна вероятности (рис. 04. 2.0.28) нахождения молекул идеального газа в единичном

V объёме пространства с x, y и z координатами, где их потенциальнаяэнергия имеет значение W_p, и одновременного нахождения проекцийv_iX, v_iY и v_iZ на Ov_X, Ov_Y и Ov_Z оси вектораv_i скоростей молекулв (рис. 04. 2.0.25) единичномV объёмескоростей с v_X, v_Y и v_Z координатами по направлению этого вектора v_i скоростей молекул.

КинетическаяW_k энергии(4.32) из раздела 04. 1.0 "Физическая термодинамика" поступательного движения молекул идеального газа m_i массой с v_i модулёмвектораv_i скоростей молекул этих молекул имеет следующий вид: W_k = mv ²/2 = m(v_X ² + v_Y ² + v_Z ²)/2.(4.287) Подставляем (4.287) в (4.286) и получаем функцию f(x, y, z, v_X, v_Y, v_Z)плотности вероятности распределения Максвелла- Больцмана, когда полная W энергия молекул идеального газа равна сумме потенциальной W_p энергии в (рис. 04. 2.0.28) произвольной точке пространства с x, y и z координатами во внешнем силовомполеи W_kкинетической энергиипоступательного движения молекул идеального газа с (рис. 04. 2.0.25) величинами проекцийv_iX, v_iY и v_iZ на Ov_X, Ov_Y и Ov_Z оси вектораv_i скоростей молекул по направлению этого вектора v_i скоростей молекул, вследствие чего эта функция f(x, y, z, v_X, v_Y, v_Z)плотности вероятности распределения Максвелла - Больцманаимеет следующий вид: f(x, y, z, v_X, v_Y, v_Z) = (n₀/N)(m/2πkT)^3/2exp [-(W_p+ W_k )/ kT].(4.288)

Случайные отклонения значений параметров в системах, находящихся в состоянии термодинамического равновесия, от их средних значений (равновесные флуктуации): средний квадрат флуктуаций кинетической энергии поступательного движения, внутреннейэнергии молекул идеального газа. Явления переноса в газах. Термодинамические потоки: определение и классификация. Тепловой поток: уравнение и коэффициент теплопроводности. Поток импульса: уравнение и коэффициент вязкости. Диффузионный поток: уравнение и коэффициент диффузии. Эффузия в разреженном газе. Условие равновесия для разреженного газа. Физический вакуум. Броуновское движение. Производство энтропии в необратимых термодинамических процессах.

Случайные отклонения значений параметров в системах, находящихся в состоянии термодинамического равновесия, от их средних значений (равновесные флуктуации): средний квадрат флуктуаций кинетической энергии поступательного движения молекул идеального газа

Система, находящаяся в состоянии термодинамического равновесия, характеризуется определённым количеством значений её параметрови, в том числе, значением X параметра с его

<X> средним значением, которым может быть (4.1), (4.2) из раздела 04.1.0 "Физическая термодинамика"P давление, v₀ удельныйобъем вещества, Tтемпература, (4.51) из раздела 04.1.0 "Физическая термодинамика" внутренняяU энергия, (4.189) из раздела 04.1.0 "Физическая термодинамика"Sэнтропияэтой термодинамическойсистемы.

Флуктуации Xпараметра определяются как ΔXотклонениеэтого Xпараметра от его

<X> среднегозначения, вследствие чего для определения ΔXфлуктуации имеет место следующее выражение: ΔX = X - <X>. (4.289)

Положительные и отрицательные ΔXфлуктуацииравновероятны, поэтому при усреднении этих ΔXфлуктуацийпо измерению большого N количества одного и того же Xпараметранаходящейся в состоянии термодинамического равновесиясистемы для определения <ΔX>среднего значения N

флуктуаций имеет место следующее выражение: <ΔX> = ∑(X_i - <X>)/N = 0,(4.290)

i = 1

где X_i - i - ое измеренное значение Xпараметра находящейся в состоянии термодинамического равновесиясистемы; N - количество измерений Xпараметранаходящейся в состоянии термодинамического равновесиясистемы, проведённые, например, в разные моменты t_i времени.

Для количественнойоценки ΔXфлуктуацийиспользуют с учётом (4.251) следующее выражение <ΔX²> среднегоквадрата флуктуаций Xпараметра: <ΔX²> = <(X - <X>)²> =

= <X² - 2X<X> + <X>²> = <X²> - 2<X<X>> + <X>² = <X²> - 2<X><X> + <X>² = = <X²> - 2<X>² + <X>² = <X²> - <X>², (4.291)

где <X²> - средний квадрат значения Xпараметра находящейся в состоянии термодинамического равновесиясистемы; <X>²- квадрат среднего значения Xпараметра находящейся в состоянии термодинамического равновесиясистемы.

Для количественнойоценки Δφ(X)флуктуацийлюбой φ(X) функции Xпараметра находящейся в состоянии термодинамического равновесиясистемы используют с учётом (4.289) следующее выражение < [Δφ(X)]²> среднегоквадрата Δφ(X)флуктуацийлюбой φ(X)функции Xпараметра:

<[Δφ(X)]²> = <[φ(X) - <φ(X)>]²> = <[φ(X)]² - 2φ(X)<φ(X)> + <φ(X)>²> =

= <[φ(X)]²> - 2<φ(X)<φ(X)>> + <φ(X)>² = <[φ(X)]²> - 2<φ(X)><φ(X)> + <φ(X)>² = = <[φ(X)]²> - 2<φ(X)>² + <φ(X)>² = <[φ(X)]²> - <φ(X)>², (4.292)

где <[φ(X)]²> - средний квадрат значения φ(X) функции Xпараметра находящейся в состоянии термодинамического равновесиясистемы; <φ(X)>² - квадрат среднего значения φ(X) функции Xпараметра находящейся в состоянии термодинамического равновесиясистемы.

Наибольшее распространение для количественной оценки ΔXфлуктуаций Xпараметра и

Δφ(X) флуктуаций функции Xпараметра находящейся в состоянии термодинамического равновесиясистемы нашли следующие выражения среднеквадратичных флуктуаций:

(<ΔX²>)^1/2 = (<X²> - <X>²)^1/2; (<[Δφ(X)]²>)^1/2 = (<[φ(X)]²> - <φ(X)>²)^1/2, (4.293)

где (<ΔX²>)^1/2 - среднеквадратичная флуктуацияXпараметранаходящейся в состоянии термодинамического равновесиясистемы; (<[Δφ(X)]²>)^1/2- среднеквадратичная флуктуация

Δφ(X) функции Xпараметранаходящейся в состоянии термодинамического равновесиясистемы.

Выражения относительных среднеквадратичных флуктуаций имеют следующий вид:

(<ΔX²>)^1/2/<X> = (<X²> - <X>²)^1/2/<X>;

(<[Δφ(X)]²>)^1/2/<φ(X)> = (<[φ(X)]²> - <φ(X)>²)^1/2/<φ(X)>, (4.294)

где (<ΔX²>)^1/2/<X> - относительная среднеквадратичная флуктуация Xпараметранаходящейся в состоянии термодинамического равновесиясистемы; (<[Δφ(X)]²>)^1/2/<φ(X)> - относительная среднеквадратичная флуктуация Δφ(X) функции Xпараметранаходящейся в состоянии термодинамического равновесиясистемы.