Статистическое описание равновесных состояний термодинамических систем: одно -, дву – и трехмерные функции распределения 2 страница
dPvX, vY, vZ = dN/N = f(v)dvXdvYdvZ. (4.248) Приравниваем правые части (4.247) и (4.248), т.к. левые части этих выражений равны, и получаем следующее выражение: f(v) = f(vX) f(vY) f(vZ) ↔ lnf(v) = lnf(vX) + lnf(vY) + lnf(vZ). (4.249) Продифференцируем правую и левую части (4.249) выражения по переменной viX - проекции на OvX осьвектораvi скоростей молекул, используя "цепное правило" дифференцирования сложной функции, вследствие чего имеет место следующее выражение: {∂[lnf(v)]/∂[f(v)]}[∂f(v)/∂v] (∂v/∂vX) = = {∂[lnf(vX)]/∂[f(vX)]}[∂f(vX)/∂vX](∂vX/∂vX) ↔ [1/f(v)][∂f(v)/∂v](∂v/∂vX) = [1/f(vX)][∂f(vX)/∂vX]. (4.250) Поскольку vi модульвектораvi скоростей молекул (1.10) из раздела 01.0 «Физические основы механики» имеет вид: vi = (viX2 + viY2 + viZ2)1/2, то частная производнаяот этого vi модуляпо переменной величине проекции viX на OvX осьвектораvi скоростей молекул в (4.250) имеет следующий вид: ∂v/∂vX = vX /(vX 2+ vY 2+ vZ 2)1/2 = vX/v. (4.251) Подставляем (4.251) в (4.250), а также подставляем (4.246) f(v) = f(vX) f(vY) f(vZ) - функцию плотности вероятности, численноравнуювероятностиодновременного (4. 227) нахождениязначений
проекций viX, viY и viZ на OvX, OvY и OvZ оси вектораvi скорости молекул (рис. 04. 2.0.25) в единичном интервале значений, тоже в (4.250), вследствие чего получаем следующее выражение:
[1/f(v)][∂f(v)/∂v]/v =[1/f(vX)][∂f(vX)/∂vX]/vX ↔ [1/f(vX) f(vY) f(vZ)][∂f(v)/∂v]/(vX 2+ vY 2+ vZ 2)1/2 =
= [1/f(vX)][∂f(vX)/∂vX]/vX, (4.252) где vi = (viX2 + viY2 + viZ2)1/2 - модульвектораvi скоростей молекул.
Праваячасть равенства (4.252) не зависит от переменных проекций viY и viZ на OvY и OvZ оси вектораvi скоростей молекул, а зависит только от переменной величины проекции viX на OvX осьвектораvi скоростей молекул. Левая часть (4.252) выражения, в которой присутствуют переменные
проекции viY и viZ на OvY и OvZ оси вектораvi скоростей молекул, вследствие равенства правойи левой частей, тоже не должна зависеть от этих переменных проекций viY и viZ на OvY и OvZ оси
вектораvi скоростей молекул. Это возможно в случае равенства левойи правойчастей
(4.252) выражения одной и той же константе, которую обозначим "-α", поэтому приравняем правую[1/f(vx)][∂f(vx)/∂vx]/vx часть (4.252) выражения "-α" постоянной величине, вследствие чего имеет место следующее выражение: [1/f(vX)][∂f(vX)/∂vX]/vX = -α ↔ [1/f(vX)][∂f(vX)/∂vX]dvX/dvX = -αvX ↔
↔ d[f(vX)]/f(vX)dvX = - αvX ↔ d[f(vX)]/f(vX) = -αvXdvX ↔ ∫d[f(vX)]/f(vX) = - α∫vXdvX ↔
↔ lnf(vX) = -αvX2/2 + lnA ↔ ln[f(vX)/A] = -αvX 2/2 ↔ f(vX) = Aexp(-αvX 2/2), (4.253) где A - постояннаяинтегрирования. Функции плотностивероятности f(vY) и f(vZ) соответственно по OvY и OvZ осям координат определяются аналогично (4.249), (4.250), (4.251), (4.252) и имеют следующий вид: f(vY) = A exp(-αvY 2/2); f(vZ) = Aexp(-αvZ 2/2). (4.254) С учётом трёхмерной(4. 228) функцииf(v) = f(vX) f(vY) f(vZ)плотности вероятности, представляющей собой произведение (4.253), (4.254) функций f(vX), f(vY), f(vZ) плотностивероятности и которая численно равна (рис. 04. 2.0.25) вероятности нахождения модуля vi вектораvi скоростей молекул в единичном прямоугольном объёме по направлению этого вектора vi скоростей молекул, а также с учётом (4.251) значения модуля скорости молекул vi = (viX2 + viY2 + viZ2)1/2, выражение (4.246) принимает следующий вид: f(v) = f(vX) f(vY) f(vZ) = A3exp[-α(vX 2/2)]exp[-α(vY 2/2)] exp[-α(vZ 2/2)] =
= A3exp[-α(vX 2 + vY 2 + vZ 2)/2] = A3 exp[-αv2/2). (4.255) Постоянная A в (4.253), (4.254) и (4.255) определяется из условия нормировки, вследствие чего имеет место следующее выражение: ∞ ∞ A ∫ exp( -αvX 2/2)dvX = 1 ↔ A(2/α)1/2∫exp(-t2)dt = 1, (4.256) -∞ -∞
где t = (α/2)1/2vX; dt = (α/2)1/2 dvX ↔ dvX =(2/α)1/2dt. Выражение (4.256) означает (рис. 04. 2.0.25) следующее: вероятность dPX нахождения
viX проекций на OvX осьвектораvi скоростей молекул в бесконечноминтервале значений скоростейпоэтойOvX оси координат равна1.
Интеграл вероятностей в (4.256) выражении имеет следующее значение:∞
∫exp(-t2)dt = π1/2. (4.257) -∞ Подставляем значение (4.257) интеграла вероятностей в (4.256) и определяем следующее выражение для A постоянной: A = (α/2π)1/2. (4.258) Функция(4.253) f(vX) - функция плотностивероятности, которая численноравна вероятности нахожденияпроекций viX на OvX ось вектораvi скоростей молекул в единичном интервале значений скоростейпоэтойOvX оси координат, c учётом значения (4.258) A постоянной принимает следующий вид: f (vX) = (α/2π)1/2exp(-αvX 2/2). (4.259) Функции(4.254) f(vY) и f(vZ) - функции плотностивероятности, которые численноравны вероятности нахождения проекций viY, viZ на OvY и OvZ оси вектораvi скоростей молекул в единичных интервалах значений скоростейпоэтимOvY и OvZ осям координат, c учётом значения (4.258)
A постоянной принимают следующий вид: f(vY) =(α/2π)1/2exp(-αvY 2/2); f(vZ) =(α/2π)1/2exp(-vZ 2/2).(4.260) Функция(4.255) f(v) плотностивероятности, которая численно равна вероятности нахождениямодуля vi вектораvi скоростей молекул в единичном прямоугольном V объёме по направлению этого вектора vi скоростей молекул,с учётом значения (4.258) A постоянной принимает следующий вид: f(v) = f(vX) f(vY) f(vZ) ↔ f(v) =(α/2π)1/2exp(-αvX 2/2)(α/2π)1/2exp(-αvY 2/2)(α/2π)1/2exp(-αvZ 2/2) ↔
↔ f(v) =(α/2π)3/2 exp[-α(vX 2 + vY2 + vZ 2)/2] = (α/2π)3/2exp[-αv2/2). (4.261) где vi2 = viX2 + viY2 + viZ2- квадрат модулявектораvi скоростей молекул. Определимсреднее< viX 2> значение квадрата viX проекций на OvX осьвектораvi скоростей молекул с использованием (4. 225) правила определения среднего< φ(x)> значенияφ(x) функции, которой в данном случае является среднее< viX 2> значение квадрата viX проекций на OvX осьвектора
vi скоростей молекул, при известной (4.259)f (vX) плотностивероятности этих viX проекций на OvX осьвектораvi скоростей молекул, с учётом чего < vX 2> среднеезначениеимеет следующий вид:
∞ ∞
< vX 2 > = ∫vX 2f(vX)dvX = (α/2π)1/2∫vX 2exp(-αvX 2/2)dvX = (α/2π)1/2(2π/α3)1/2 = 1/α. (4.262)
0 0 Средние< vY2>, < vZ 2> значения квадратов проекций viY и viZ на оси OvY и OvZ вектора
vi скоростей молекул по аналогии с (4.262) выражением имеют следующий вид:
< vY 2> = 1/α; < vZ 2> = 1/α. (4.263) Среднее<v2> значение квадрата модуля vi2 вектораvi скоростей молекул или(4.33) из раздела
04.1.0 "Физическая термодинамика" квадрат среднейvквквадратичной скорости молекул с учётом (4.262), (4.263) принимает следующий вид: <v2> = vкв2 = < vX 2 > + < vY 2> + < vZ 2> = 3/α. (4.264) Приравниваем (4.264) среднее<v2> значение квадрата модуля vi 2 вектораvi скоростей молекул и vкв = (3kT/mi)1/2 выражение(4.33) из раздела 04.1.0 "Физическая термодинамика" квадрата средней
vквквадратичной скорости молекул и получаем следующее α значениеконстантывэтом (4.264) выражении: 3/α = 3kT/m ↔ α = m/kT, (4.265) где m - масса молекулы, k - постоянная Больцмана, а T - термодинамическаятемпература идеального газа.
Подставляем (4.265) α значениеконстантыв (4.262), (4.263), (4.264) и получаем следующие окончательныевыражения для (рис.4.25) функций f(vX), f(vY) и f(vZ) плотностивероятности проекций viX, viY и viZ на OvX, OvY и OvZ оси вектораvi скоростей молекул, а также получаем следующее окончательноевыражение функции f(v) плотностивероятности vi модуля вектораvi скоростей молекул по направлению этого вектора vi скоростей молекул:
f (vX) = (m/2πkT)1/2exp( -mvX 2/2kT); f(vY)=(m/2πkT)1/2exp(-m vY 2/2kT); f(vZ)=(m/2πkT)1/2exp(-mvZ 2/2kT); f (v) = (m/2πkT)3/2 exp( -mv2/2kT). (4.266) C учётом окончательного(4.266)выражения для функции f(v) плотностивероятности vi модуля вектораvi скоростей молекул по направлению этого вектора vi скоростей молекул, вероятность dPv нахождения vi модулей вектораvi скоростей молекул в элементарном шаровом (рис.4.25) слое dVv объёмом с внутренним и внешнимирадиусами соответственно v; v + dv имеет следующий вид: dPv = f(v)4πv2dv = (m/2πkT)3/2exp(-mv2/2kT) 4πv2dv = F(v)dv ↔ F(v) = dPv/dv, (4.267) где F(v) = (m/2πkT)3/2exp( -mv2/2kT)4πv2 - функция (4. 243) плотности вероятности (4. 221), которая численно равна (рис.04.2.0.25) вероятности нахождения vi модуля вектораvi скоростей молекул в шаровомслое с внутренним радиусом, равным этомуvi модулю вектораvi скоростей молекул, и толщиной, равной единичному интервалу, например, находящихся в интервале vi модулей вектораvi скоростей молекул 500…501 м/с по всемвозможным направлениямэтих векторовvi скоростей молекул.
Среднее <v> арифметическоезначениеvi модулей вектораvi скоростей молекул с использованием (4. 225) правила определения среднего< φ(x)> значенияφ(x) функции, которой в данном случае является vi модуль вектораvi скоростей молекул, при известной (4.267) функции F(v) плотности вероятности имеет следующий вид:
∞ ∞
<v > = ∫vF(v)dv =(m/2πkT)3/24π∫ exp(-mv2/2kT)vdv = (8kT/πm)1/2, (4.268) 0 0 где интегрированиепроизведено по частям с помощью ξ = v2 подстановки; пределы интегрирования от 0 до ∞ соответствуют всем возможным значениям vi модулей векторовvi скоростей молекулидеального газа.
Функция (4.267) плотности F(v) вероятности, которая численно равна вероятности нахождения vi модулей векторовvi скоростей молекул в шаровомслое с внутренним радиусом, равным этомуvi модулю вектораvi скоростей молекул, и толщиной, равной единичному интервалу скоростей, по всемвозможным направлениямэтих векторовvi скоростей молекул имеет максимумпри наиболее vвервероятноммодуле этих векторовvi скоростей молекул.
Взяв первую производнуюdF(v)/dvи приравняв её нулю, определим следующий наиболее vвервероятныймодуль векторовvi скоростей молекул:
dF(v)/dv|v=vвер = exp(-mvвер 2/2kT)(2 - mvвер2/kT) vвер = 0 ↔ vвер = (2kT/m)1/2, (4.269) Число dNv молекул, имеющих vi модуливектораvi скоростей молекул(рис. 04. 2.0.25) и находящихсяв (4. 241) dVv = 4πv2dvэлементарном шаровом слое с внутренним радиусом, равным
vi модулю вектораvi скоростей молекул, и толщиной этогошаровогослоя, равной dv элементарному приращению vi модулей скоростейпо всемвозможным направлениямвекторовvi скоростей молекул, c учётом (4.243) определяется следующим выражением: dNv = NdPv = Nf(v)dVv = Nf(v)4πv2dv = NF(v)dv = N(m/2πkT)3/2exp(-mv2/2kT) 4πv2dv, (4.270)где N - полное число молекул в данной массе газа, в которой измеряются vi модульвекторовvi скоростеймолекул; dVv - объём (рис. 04. 2.0.25) элементарногошарового слоя v радиусоми dv толщиной. Выражение (4.270) называется распределениемМаксвелла молекул по скоростям.
На рис. 04. 2.0.26 представлена графическая зависимость (4.267) плотности F(v) вероятности, которая численно равна вероятности нахождения vi модулей векторовvi скоростей молекул
O2 кислорода, имеющего T1 = 300 К или T2 = 600 К температуру, в шаровомслое с внутренним радиусом, равным этомуvi модулю вектораvi скоростей молекул, и толщиной, равной единичному интервалу скоростей, по всемвозможным направлениямэтих векторовvскоростей молекул
O2 кислорода.
Соотношения (рис. 04. 2.0.26) между наиболее (4.269) vвервероятныммодулём векторов
vi скоростей молекул O2 кислорода, средним (4.268) <v> арифметическимзначением модулей векторовvскоростей и средней(1.1) из раздела 1.0 "Физические основы механики"
vквквадратичной скоростью этих молекул O2кислорода определяется следующим выражением: vвер: <v>: vкв = (2)1/2: (8/π)1/2: (3)1/2 = 1 : 1,13: 1,22. (4.271)
Результаты расчёта наиболее (4.269) vвервероятногомодуля векторовvi скоростей молекул
O2 кислорода, среднего (4.268) <v> арифметическогозначения модулей векторовvi скоростей и средней(4.33) из раздела 04.1.0 "Физическая термодинамика"vквквадратичной скоростью этих молекул O2кислородадля двухT1 = 300 К и T2 = 600 Ктемпературэтогогаза, принятого идеальным,приводятся в таблице.
|
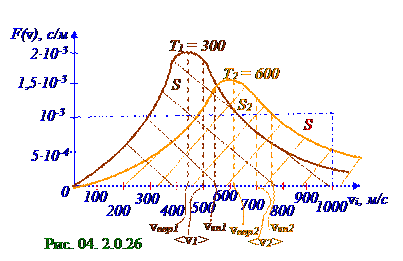
Таблица: значения скоростей vвер, <v>, vкв и соответствующие этим скоростям F(v) плотности вероятности
| T, К | vвер, м/с | F(vвер), с/м | <v>, м/с | F(<v>), с/м | vкв, м/с | F(vкв), с/м |
| 300 | 442 | 2∙10-3 | 500 | 1,75∙10-3 | 540 | 1,6∙10-3 |
| 600 | 618 | 1,6∙10-3 | 700 | 1,5∙10-3 | 756 | 1,4∙10-3 |
Функция распределения по значениям кинетической энергии поступательного движения молекул идеального газа
Выражение vi модуля вектораvi нерелятивистской из раздела 03.0.0 "Релятивистская механика" поступательнойскорости i-ой молекулыидеального газачерез их Wki кинетическую(4.32) из раздела 04.1.0 "Физическая термодинамика"энергию и mi массу имеет следующий вид: v = (2Wk/m)1/2 ↔ dv = (2mWk)-1/2dWk. (4.272)Подставляем (4.272)в (4.270) и получаем dNW число молекул идеального газа, кинетическая энергия которых заключена в интервале от Wk до Wk +dWk, т.е. получаем следующеераспределениемолекул по значениям их Wkкинетических энергий:
dNW = N(m/2πkT)3/2exp(-mv2/2kT) 4πv2dv = N(m/2πkT)3/2{exp[(-m2Wk/m)/2kT]}4π(2Wk/m)(2mWk)-1/2dWk =
= N(m/2πkT)3/2[exp(-Wk/kT)]4π[(2Wk)1/2/m3/2] = N[2π/(πkT)3/2] [exp(-Wk/kT)] Wk1/2dWk, (4.273)
где N - полное число молекул в данной массеидеального газа, в которой измеряются Wkкинетическиеэнергиимолекул; k - постоянная Больцмана; T - термодинамическаятемпература идеального газа.
Вероятность (4. 221) dPW того, что Wkкинетическая энергия молекул идеального газа заключена в интервале от Wk до Wk +dWk,равна отношению dNW числа молекул идеального газа, кинетическая энергия которых заключена в этом интервале от Wk до Wk +dWk, к полному N числу молекул в данной массеидеального газа, вследствие чего для определения вероятности dPW с учётом(4.235)имеет место следующее выражение: dPW = dNW/N =[2π/(πkT)3/2] [exp(-Wk/kT)] Wk1/2dWk. (4.274)
Функция (4. 221) плотности f(Wk) = dPW /dWk вероятностиWkкинетической энергии молекул идеального газа, которая численно равна вероятности нахождения этой Wkкинетической энергии молекул в единичному интервале значений, например, находящихся в (6…7)10-21Дж интервале, имеет с учётом(4.274) следующий вид: f(Wk) = dPW /dWk =[2π/(πkT)3/2] [exp(-Wk/kT)] Wk1/2. (4.275)
Экспериментальная проверка распределения Максвелла по абсолютным значениям скоростей молекул идеального газа (опыт Ламмерта)
Прямыеизмерения скорости атомовртути в пучке были выполнены в 1929 г.Ламмертом. Два (рис. 04. 2.0.27) 6 диска, насаженные на общую ось, имели радиальные3 прорези, сдвинутые одна относительно другой на φ угол. Напротив прорезей находилась 1 печь, в которой легкоплавкийметалл нагревался до высокой температуры. Разогретые7 атомыметалла, в данном случае ртути, вылетали из 1печи и с помощью 2 коллиматоранаправлялись в необходимом направлении. Наличие
2 коллиматора обеспечивало движение 7 атомов металла между быстро вращающимися с (1.19) из раздела 01.0 «Физические основы механики» ωциклической частотой 6 дисками по прямолинейной
4 траектории, параллельной их оси.
В установке Ламмертас целью увеличения интенсивностипрошедшего пучка в 6 дисках было сделано множество прорезей, которые для упрощения на рис. 04. 2.0.27 не изображены. Атомы
7 металла, пролетевшие через прорези в 6 дисках, регистрировали с помощью 5 детектора. Всю описанную установку помещали в глубокий вакуум.
Дата добавления: 2016-02-14; просмотров: 597;
