Практична робота. Розрахунок сил затискання у верстатних пристроях 3 страница
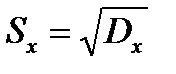 .
.
Для оцінювання розсіювання випадкових величин за допомогою безрозмірної (відносної) характеристики використовують коефіцієнт варіації,що дорівнює відношенню середнього квадратичного відхилення до математичного сподівання:
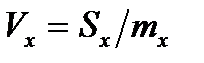 .
.
Порядок виконання
1. Відповідно до табличних даних, визначених в табл. 10.2. розрахувати математичне сподівання, дисперсію, середнє квадратичне відхилення, коефіцієнт варіації.
2. Для визначених в практичному занятті 10 закону розподілу побудувати графічні залежності 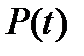 ,
, 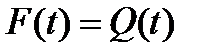 ,
, 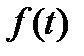 .
.
3. Для самостійної роботи рекомендується додатково вирішити задачі, наведені в додатку 11 в таблиці Д.11.1.
Приклад виконання.
Розрахуємо математичні характеристики закону розподілу закону розподілу (практична робота 10) з врахуванням даних табл. 10.1
Математичне сподівання оцінюємо за формулою
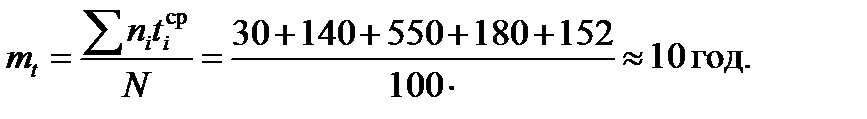
Дисперсію оцінюємо за формулою
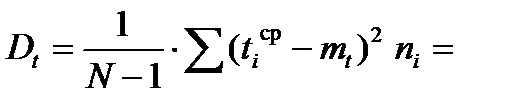
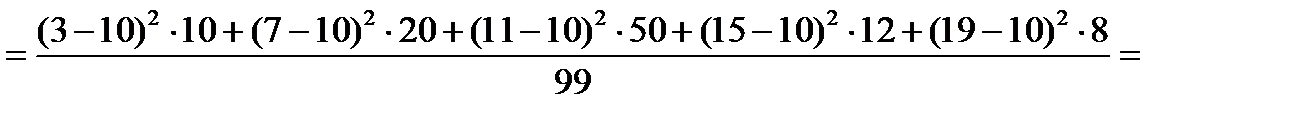
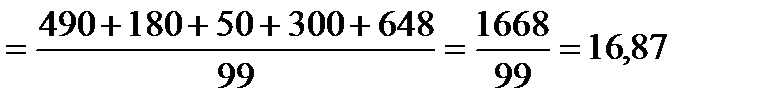
Середньоквадратичне відхилення
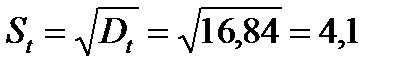 .
.
Коефіцієнт варіації
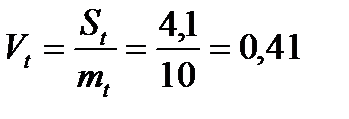 .
.
За результатами розрахунків, наведених в табл.10.1 будуємо графічні залежності показників надійності колінчастого вала холодильного компресора.
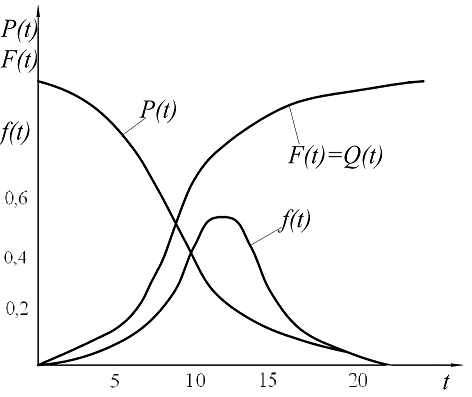
Рис. 11.1. Показники надійності колінчастого вала холодильного компресора: 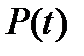 – імовірність безвідмовної роботи;
– імовірність безвідмовної роботи; 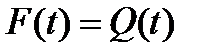 – імовірність відмови;
– імовірність відмови; 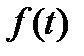 – функція щільності розподілу випадкової величини
– функція щільності розподілу випадкової величини
11.4. Контрольні запитання
1) Як розраховується математичне сподівання та його зв'язок з оцінкою середнього значення 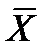 .
.
2) Що таке дисперсія і що вона означає?
3) Яка особливість розрахунку дисперсії для безперервних та дискретних величин?
4) З якою метою вводиться показник середнього квадратичного відхилення?
5) Як пов’язані між собою характеристики графічних залежностей P(t) та F(t).
12. Практична робота. Використання інформаційних технологій для розрахунків показників надійності виробів
12.1. Завдання. Розрахувати показники надійності виробів з використанням програми «Microsoft Excel». Варіант роботи вибирають в практичній роботі 10.
12.2. Хід виконання роботи
1. Перше що треба зробити — це упорядкувати значення напрацювань на відмову у порядку зростання. Для цього відкриваємо програму Microsoft Excel та вводимо ці значення в стовпчик. Потім виділяємо отриманий стовпчик. Для цього переміщуємо курсор миші на перше значення стовпчика та, натиснувши ліву кнопку миші, переміщуємо курсор миші в кінець стовпчика не відпускаючи кнопку миші. Потім знаходимо на панелі інструментів кнопку

(Сортировка по возрастанию) та натискуємо її. Якщо така кнопка на панелі відсутня, то необхідно виконати такі дії:
1) вибрати в основному меню пункт Сервис→Настройка…(рис.12.1);
Рис. 12.1
2) у діалоговому вікні, що з’явилося, необхідно вибрати другу закладку (Команды). У лівому вікні вибрати пункт Данные (рис. 12.2).
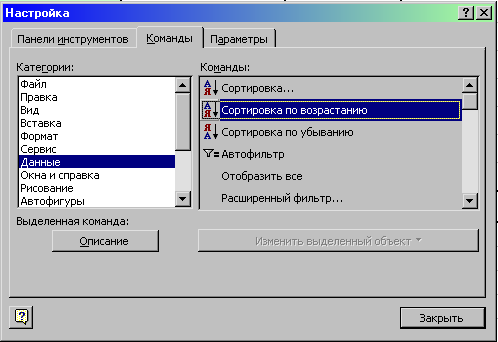
Рис. 12.2
У правому полі знаходимо кнопку

(Сортировка по возрастанию) наводимо курсор миші на неї та натиснувши ліву кнопку миші, перетягаємо цю кнопку у зручне місце на панелі інструментів.
2.Отримавши впорядковані за зростанням значення, потрибно розбити їх на однакові інтервали. Довжина кожного інтервалу:
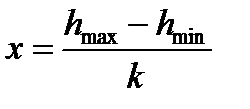 ,
,
де 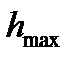 та
та 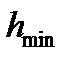 — максимальне та мінімальне значення напрацювання;
— максимальне та мінімальне значення напрацювання; 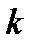 — кількість інтервалів для зручності доцільно прийняти кількість інтервалів, яка дорівнює 10.
— кількість інтервалів для зручності доцільно прийняти кількість інтервалів, яка дорівнює 10.
3.На новому аркуші у комірку А1 вводимо текст “Границі інтервалу ”. У комірку А2 вводимо мінімальне значення напрацювання на відмову. У комірці В2 пишемо “=А2+х”, де х — довжина інтервалу. У комірку А3 пишемо “=В2”. У комірці В3 пишемо “=А3+х”. У комірці А4 пишемо “=В3”. У комірці В4 пишемо “=А4+х” і так далі, поки не отримаємо потрібну кількість інтервалів (10 інтервалів).
Після введення даних у комірку необхідно натискати Enter (8 )
У комірках А2 — А11 будуть початки інтервалів, у комірках В2 — В11 — кінці інтервалів. Отримані результати матимуть вигляд, наведений на рис. 12.3.
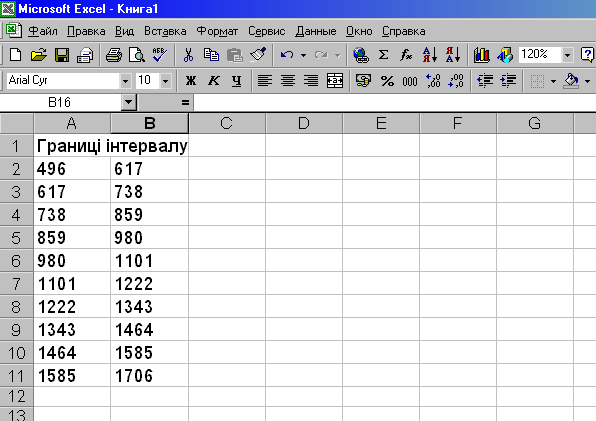
Рис. 12.3
4. Підраховуємо частоту в інтервалі та записуємо відповідні значення у комірки С2—С11.У комірці С1 пишемо “Частота в інтервалі”.
5. Знаходимо середину кожного інтервалу. Вводимо в комірку D1 “Середина інтервалу”. У комірку D2 вводимо “=(В2+А2)/2”, у комірку D3 “=(В3+А3)/2”, у комірку D4 “=(В4+А4)/2” і так далі, до “=(В11+А11)/2”. Щоб прискорити знаходження середини інтервалів, можна ввести у комірку D2 “=(В2+А2)/2” потім виділити комірку D2, натиснувши на панелі інструментів кнопку

(“Копировать”), потім виділити комірки D3—D11 та натиснути на панелі інструментів кнопку

“Вставить”. Отримані результати матимуть вигляд, наведений на
рис. 12.4.
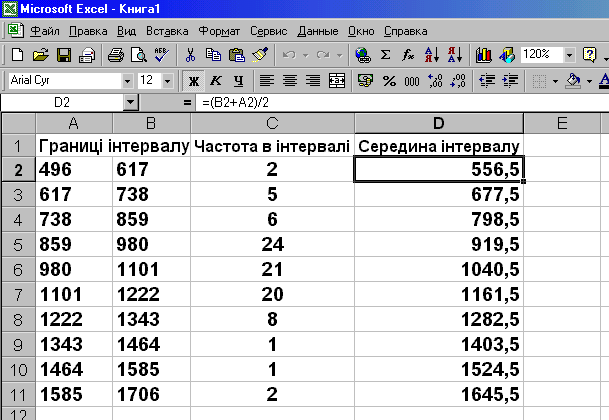
Рис. 12.4
6. У комірці В12 пишемо “Всього”. Потім виділяємо комірки С2—С11 та на панелі інструментів натискаємо кнопку
(Автосумма).
7.Розраховуємо частоту в інтервалі Wi. У комірці Е1 пишемо “Частота,Wi=”. У комірку Е2 вводимо “=С2/С12”, у комірку Е3 вводимо “=С3/С12”, у комірку Е4 “=С4/С12” і так далі до “=С11/С12”. У комірці D12 пишемо ∑Wi, потім виділяємо комірки Е2-Е11 та натискаємо на панелі інструментів кнопку 
(Автосумма). Значення, що з’явилося у комірці Е12, повинно дорівнювати одиниці. Отримані результати матимуть вигляд, поданий на рис. 12.5.
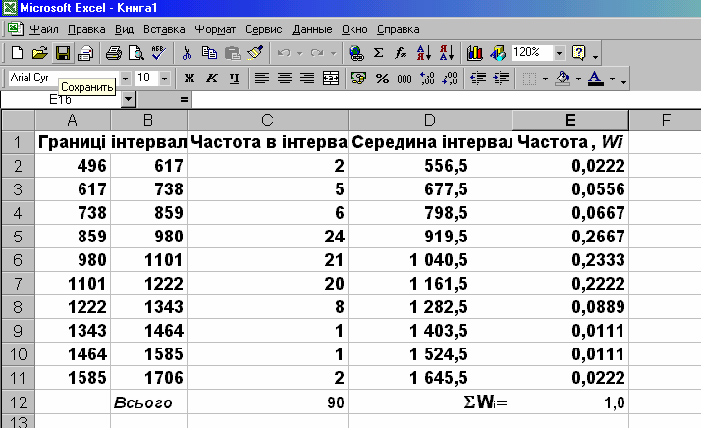
Рис. 12.5
8.Знаходимо значення F(t). У комірці F1 пишемо F(t), у комірці F2 пишемо “=Е2”, У комірці F3 пишемо “=Е3+F2”, у комірці F4 “=E4+F3”, у ячейці F5 “=E5+F4” і так далі до “E11+F10”.
9. Знаходимо значення Р(t). У комірці G1 пишемо Р(t). У комірці G2 пишемо “1- F2”, у комірці G3 “1- F3”, у комірці G4 “1- F4” і так далі до“1-F11”. Значення у комірці G11 має дорівнювати нулю. Отримані результати подані на рис. 12.6.
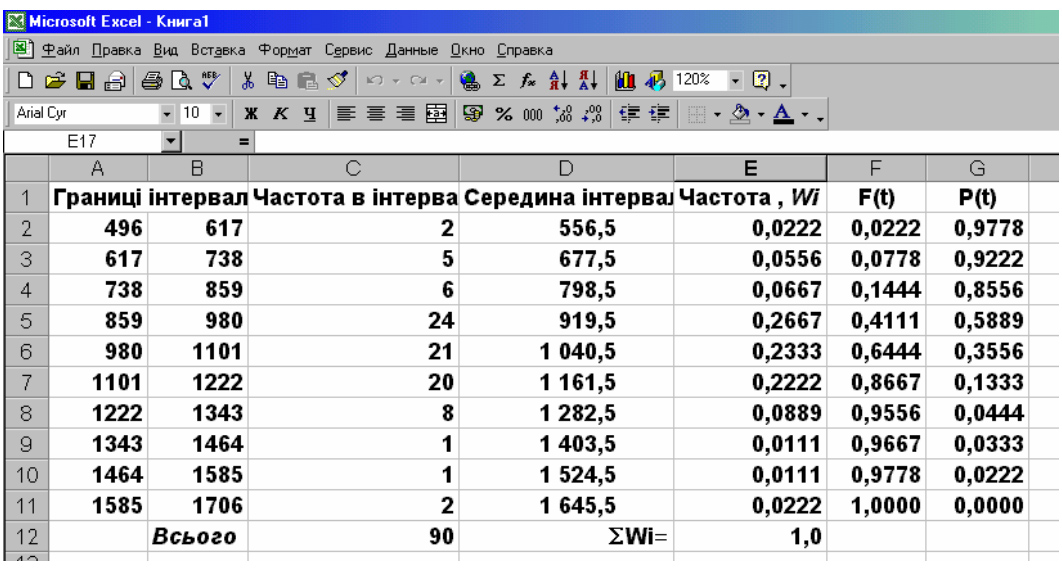
Рис. 12.6
10. Будуємо полігон. Натискаємо на панелі інструментів клавішу

(Мастер диаграмм). У діалоговому вікні, котре з’явилося в лівому вікні “Тип”, вибираємо пункт “Графік”, у правому вікні “Вид” вибираємо перший вид графіків (рис. 12.7).
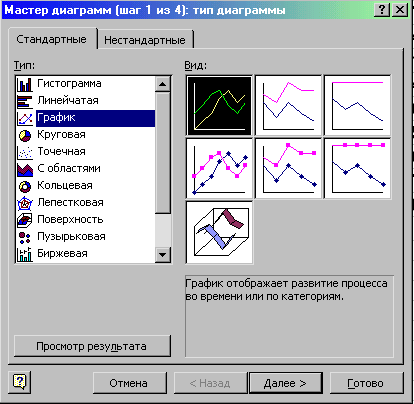
Рис. 12.7
Натискаємо кнопку “Далее>”. У вікні, що з’явилося, вибираємо другу закладку “Ряд”. Натискаємо кпопку “Добавить”. Напроти пункту “Значения” натискаємо кнопку

виділяємо комірки С2 - С11 та натискаємо кнопку

у вікні, що з’явилося. Напроти пункту “Подписи оси Х” натискаємо кнопку

виділяємо комірки D2-D11 та знову натискаємо кнопку

у вікні, що з’явилося. Натискаємо кнопку “Далее>”(Рис. 12.8).
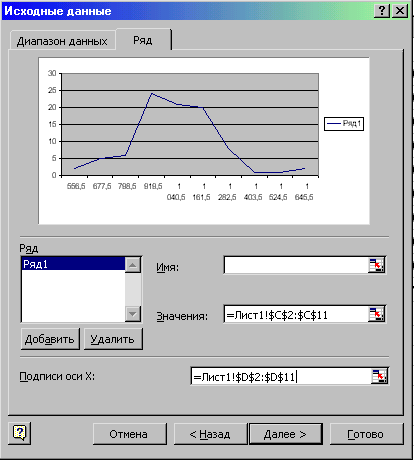
Рис 12.8.
У вікні, що з’явилося, вибираємо закладку “Линии сетки” (рис. 12.9) та ставимо галочки напроти пунктів “Основные линии” та “Промежуточные линии” осі Х та У. В закладці “Легенда” вимикаємо галочку біля пункту “Добавить легенду”. В закладці “Заголовки” в пункті “Название диаграммы” пишемо “Полігон” та натискаємо кнопку “Далее>”.
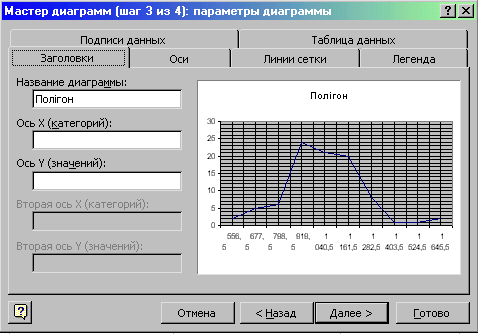
Рис. 9
У вікні, що з’явиться, вибираємо “Поместить диаграмму на листе отдельном”, у вікні напроти пункту “отдельном” замість “Диаграмма1” пишемо “Полігон” та натискаємо кнопку “Готово” (рис. 12.10).
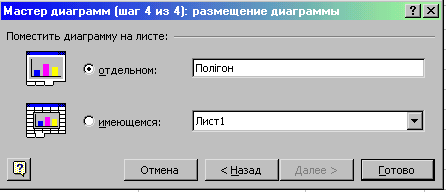
На окремому аркуші отримаємо графік. Внизу вікна Microsoft Excel з’явилася закладка “Полігон” (рис. 12.11).

Рис. 12.11
11.Будуємо гістограму.
Натискаємо на панелі інструментів клавішу

(Мастер диаграмм). У діалоговому вікні, котре з’явилося в лівому вікні “Тип”, вибираємо пункт “Гистограмма”, в правому вікні “Вид” вибираємо перший вид гістограм (рис. 12.12)
Рис. 12.12
Натискаємо кнопку “Далее>”. У вікні, що з’явилося вибираємо другу закладку “Ряд". Натискаємо кнопку “Добавить”. Напроти пункту “Значения” натискаємо кнопку

виділяємо комірки Е2— Е11 та натискаємо на кнопку

у вікні, що з’явилося. Напроти пункту “Подписи оси Х” натискаємо кнопку

виділяємо комірки D2 — D11 та знову натискаємо на кнопку

у вікні, що з’явилося. Натискаємо на кнопку “Далее>”.
Рис. 12.13
У вікні, що з’явилося, вибираємо закладку “Легенда” та вимикаємо галочку біля пункту “Добавить легенду”. У закладці “Заголовки” в пункті “Название диаграммы” пишемо “Гістограма” та натискаємо кнопку “Далее>”. Розміщуємо гістограму на окремому аркуші(рис. 12.14)
Рис. 12.14
На отриманій діаграмі наводимо курсор миші на один з стопчиків та натискаємо праву кнопку миші. У діалоговому вікні що з’явилося вибираємо пункт “Формат рядов данных…” (рис. 12.15) У закладці “Параметры” в пункті “Ширина зазора” вводимо 0.
Рис. 12.15
12.Будуємо графіки P(t), F(t) та f(t).
Натискаємо на панелі інструментів клавішу

(Мастер диаграмм). У діалоговому вікні, котре з’явилося в лівому вікні “Тип”, вибираємо пункт “Графік”, в правому вікні “Вид” вибираємо перший вид графіків(рис. 12.16).

Рис. 12.16
Натискаємо кнопку “Далее>”. В вікні, що з’явилося, вибираємо другу закладку “Ряд”. Натискаємо кпопку “Добавить”. Напроти пункту “Значения” натискаємо кнопку

виділяємо комірки G2—G11 та натискаємо на кнопку

у вікні, що з’явилося. Напроти пункту “Подписи оси Х” натискаємо кнопку

виділяємо комірки D2— D11 та знову натискаємо кнопку

у вікні, що з’явилося. У пункті “Имя” пишемо “P(t)” та знову натискаємо кнопку “Добавить”. Напроти пункту “Значения” натискаємо кнопку

виділяємо комірки F2— F11 та натискаємо кнопку

у вікні, що з’явилося. У пункті “Имя” пишемо “F(t)”. Додаємо ще один ряд, напроти пункту “Значения” натискаємо кнопку

виділяємо комірки Е2—Е11 та натискаємо кнопку

у вікні що з’явилося. У пункті “Имя” пишемо “f(t)”. Натискаємо кнопку “Далее>”.
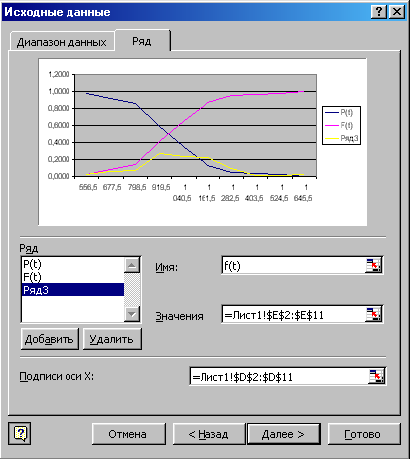
Рис. 12.17
У вікні, що з’явилося, вибираємо закладку “Линии сетки” та ставимо галочки напроти пунктів “Основные линии” та “Промежуточные линии” осі Х та У. Натискаємо на кнопку “Далее>”. У вікні, що з’явиться, вибираємо “Поместить диаграмму на листе отдельном”, у вікні напроти пункту “отдельном” замість “Диаграмма1” пишемо “Графіки” та натискаємо кнопку “Готово”. Для того, щоб зробити ці графіки плавними, наводимо курсор миші на одну з кривих графіка та натискаємо праву клавішу миші. У діалоговому вікні вибираємо пункт “Формат ряда данных”. Вибираємо закладку “Вид” та ставимо галочку біля пункту “Сглаженная линия”. Повторюємо цю операцію і для інших двох графіків. Також у діалоговому вікні “Формат ряда данных” ми можемо змінити колір графіків, вибрати форму та колір маркерів точок данних, змінити тип та товщину ліній. Отримані результати матимуть вигляд, поданий на рис. 12.18.
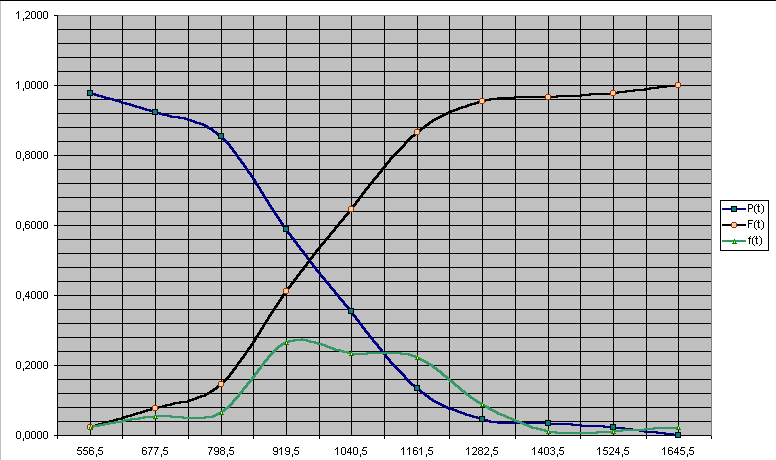
13. Оцінку математичного сподівання визначимо за формулою:
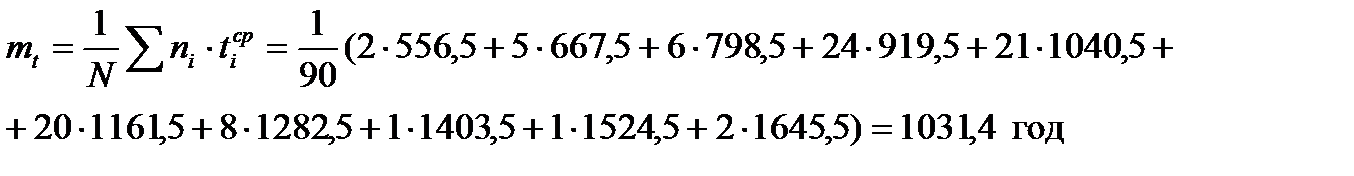
Для автоматичного розрахунку у комірку А14вводимо “Оцінка математичного сподівання:”. У комірці А15 пишемо“mt=”, а у комірку В15вводимо формулу.
“=(D2*C2+D3*C3+D4*C4+D5*C5+D6*C6+D7*C7+D8*C8+D9*C9+D10*C10++D11*C11)/C12”.
У комірці С15 пишемо “год”.
14. Оцінку дисперсії знаходимо за формулою
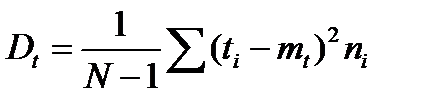 .
.
У комірку А16 вводимо “Оцінка дисперсії:”. У комірці А17 пишемо “Дt=”. У комірку В17 вводимо формулу
“=((C2*(D2-B15)^2)+(C3*(D3-B15)^2)+(C4*(D4-B15)^2)+(C5*(D5-B15)^2)+(C6*(D6-B15)^2)+(C7*(D7-B15)^2)+(C8*(D8-B15)^2)+
(C9*(D9-B15)^2)+(C10*(D10-B15)^2)+(C11*(D11-B15)^2))/(C12-1)”
15.Середньоквадратичне відхилення знаходимо за формулою
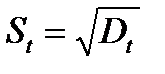 .
.
У комірку А18вводимо “Середньоквадратичне відхилення:”. У комірці А19 пишемо “St=”. У комірку В19 вводимо формулу: “=B17^0,5”.
16.Знаходимо коефіцієнт варіації:
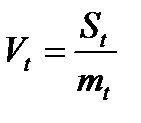 .
.
У комірку А20вводимо “Коефіцієнт варіації:”. У комірці А21 пишемо “Vt=”. У комірку В21 вводимо формулу “=B19/B15”.
Отримані результати наведено на рис. 12.19.
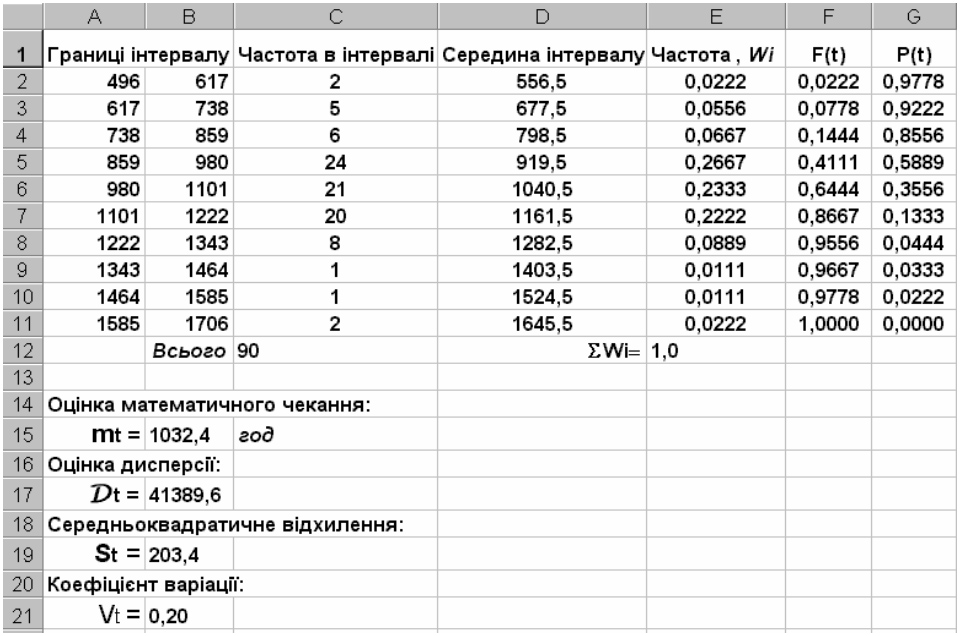 Рис. 12.19
Рис. 12.19
13. Практична робота. Розрахунок надійності технічних систем
13.1. Завдання.Розрахувати надійність технологічних схем у вигляді технічних систем підприємств харчової промисловості.
13.2. Теоретичні відомості про технічні системи та їх розрахунок
Технічні й технологічні системи з огляду на їх надійність є складними комплексами, скомпонованими в найрізноманітніших комбінаціях з окремих підсистем та елементів, що відрізняються між собою важливістю показників надійності та їхнім рівнем. Тому задачі визначення показників надійності таких систем багатоваріантні, але в їх розв’язанні можна виокремити два основних принципи:
Будують структурну схему надійності системи і визначають показники її надійності з урахуванням впливу на ці показники всіх без винятку елементів системи, тобто здійснюють повне визначення надійності;
Будують структурну схему надійності системи і за завчасно заданим критичним рівнем показників надійності елементів виділяють ті з них, що мають низьку надійність, яка є визначальною для системи в цілому. Надійність системи визначають за надійністю цих елементів, тобто розраховують надійність системи за визначальними елементами.
Системи можуть складатися з елементів, які діють послідовно (послідовна система), і з елементів, що діють паралельно (паралельна система, або система з резервуванням). Комбіновані системи можуть мати ділянки з послідовною та паралельною дією елементів.
13.2.1. Надійність послідовних систем
У техніці більшість становлять послідовні системи. Прикладом такої системи може бути привід будь-якого засобу механізації (рис. 13.1).
| • • • |
У послідовних системах відмова будь-якого зі складових елементів призводить до відмови всієї системи, а тому ймовірність безвідмовної роботи системи в цьому разі визначається множенням імовірностей безвідмовної роботи складових елементів:
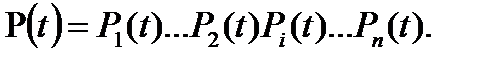 (13.1)
(13.1)
Якщо ймовірність безвідмовної роботи всіх елементів є однаковою, то
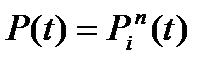 . (13.2)
. (13.2)
Отже, чим більше складових елементів, тим нижчою є надійність такої системи. Наприклад, система з 10 послідовних елементів, імовірність безвідмовної роботи кожного з яких становить 0,9, має загальну ймовірність безвідмовної роботи 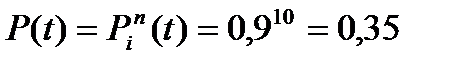 , тобто дуже низьку.
, тобто дуже низьку.
Найчастіше ймовірність безвідмовної роботи елементів досить висока, а тому простіше визначати її через імовірність відмов, використовуючи методи наближених обчислень:
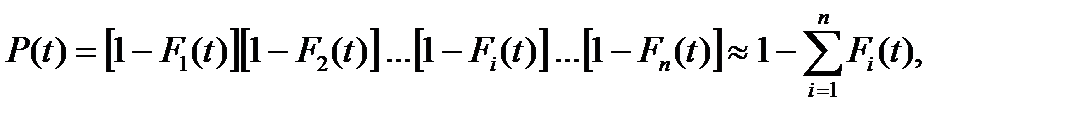 (13.3)
(13.3)
оскільки добутком двох малих величин можна знехтувати.
13.2.2. Надійність паралельних систем (систем з резервуванням)
Для підвищення надійності складних відповідальних систем, де цього не вдається досягти за рахунок надійності складових елементів, застосовують резервування.
При постійному резервуванні з навантаженням («гарячим») резервом резервні елементи або ланцюги елементів підключать паралельно до основних (рис. 13.2). Імовірність відмови всієї системи визначають за теоремою множення ймовірностей:
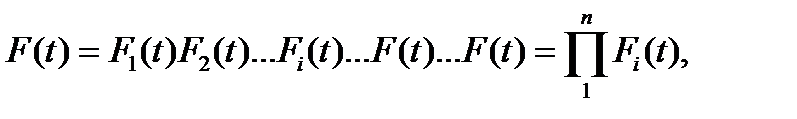 (13.4)
(13.4)
де 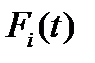 - ймовірність відмови і-го елемента.
- ймовірність відмови і-го елемента.
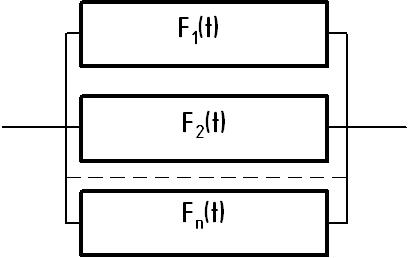
Рис. 13.2. Система з резервуванням
Тоді ймовірність безвідмовної роботи системи:
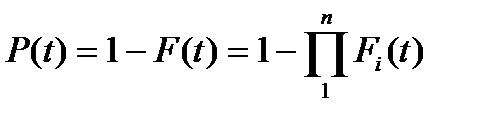 . (5.7)
. (5.7)
Якщо елементи системи рівнозначні, то
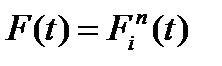 ;
; 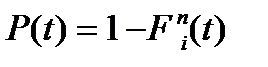 (5.8)
(5.8)
Ці залежності у загальному вигляді характеризують гаряче резервування. Наприклад, якщо при гарячому резервуванні 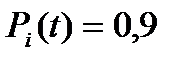 і n = 2, то
і n = 2, то 
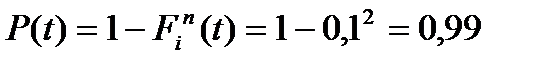 , а отже, безвідмовність системи підвищується.
, а отже, безвідмовність системи підвищується.
Інші види резервування мають свої особливості, які впливають на розрахунки. При холодному резервуванні, тобто резервуванні заміщенням, резервні елементи вступають у дію тільки після відмови основних. Резервні елементи можуть включатися в дію автоматично або вручну, а ті елементи, що відмовили, відновлюються або замінюються. У цьому разі для основного експоненційного закону розподілу відмов (за високої надійності складових елементів) імовірність відмови системи становить:
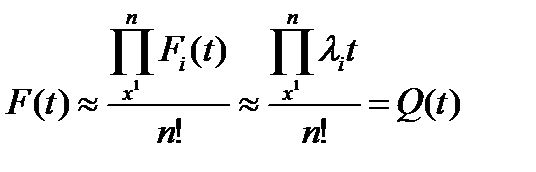 . (13.5)
. (13.5)
Для рівнозначних елементів
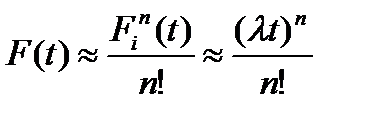 . (13.6)
. (13.6)
Ці формули (13.5), і (13.6) справедливі за умови, що надійність включення резерву гарантується повністю.
13.2.3. Надійність комбінованих систем
Комбіновані системи охоплюють ділянки з послідовно і паралельно діючими складовими елементами. Якщо в системі а елементів не дубльовані і b елементів дубльовані (рис. 13.3), то ймовірність безвідмовної роботи системи визначають за формулою
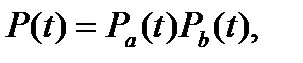 (13.7)
(13.7)
де 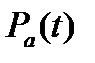 ,
, 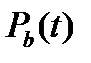 - ймовірність безвідмовної роботи ділянок відповідно з послідовно і паралельно діючими елементами.
- ймовірність безвідмовної роботи ділянок відповідно з послідовно і паралельно діючими елементами.
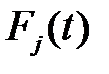
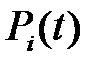
| а |
| bв |
Рис. 13.3. Комбінована система з послідовним і паралельним з’єднанням елементів
При послідовному з’єднанні елементів
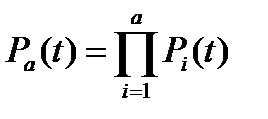 . (13.8)
. (13.8)
Для повного гарячого резервування
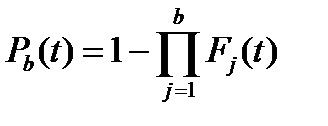 (13.9)
(13.9)
Для інших видів резервування надійність ділянок з паралельно діючими елементами b розраховують методами, викладеними раніше.
У харчових виробництвах часто застосовують комбіновані системи, які не можуть належати ні до послідовних, ні до паралельних (складні комбіновані системи). Така система може бути, наприклад, у технологічній схемі цукрового виробництва, де інколи паралельні лінії перекачування технологічних рідин мають додатковий насос, який за потреби може бути резервом для будь-якої лінії. Розглянемо такий випадок. Основна система (рис. 13.4) із елементів 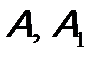 здубльована системою з елементів
здубльована системою з елементів 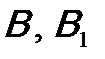 , для яких передбачений елемент С, що резервує елементи А і В.
, для яких передбачений елемент С, що резервує елементи А і В.
А 
|
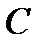
|
В 
|
В1 
|
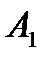
|
Рис. 13.4. Складна комбінована система
У розрахунках подібних складних систем використовують теорему Байєса, яку для визначення надійності формулюють так: імовірність відмови системи F = F (C дієздатний) 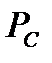 + F (C недієздатний)
+ F (C недієздатний) 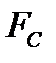 , де
, де 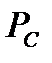 і
і 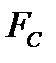 - імовірності відповідно безвідмовної роботи і відмови резерву С.
- імовірності відповідно безвідмовної роботи і відмови резерву С.
Дата добавления: 2016-03-15; просмотров: 796;
