Практична робота. Розрахунок сил затискання у верстатних пристроях 2 страница
Ремонтопридатність – властивість об’єкта бути пристосованим до підтримання та відновлення стану, в якому він здатний виконувати потрібні функції за допомогою ТО та ремонту.
Збережуваність – властивість об’єкта зберігати в заданих межах значення параметрів, що характеризують здатність об’єкта виконувати необхідні функції під час і після зберігання та транспортування.
Готовність – властивість об’єкта бути здатним виконувати потрібні функції в заданих умовах у будь-який час чи протягом заданого інтервалу часу за умови забезпечення необхідними зовнішніми ресурсами.
Ця властивість залежить від поєднання властивостей безвідмовності, ремонтопридатності, а також від матеріально-технічного забезпечення його ТО і ремонту.
Перш ніж перейти до розгляду інших понять і визначень, які охоплює надійність, зазначимо, що вона формується на етапах проектування і виготовлення виробів, а проявляється і забезпечується на етапі їх експлуатації. Технічна властивість виробів виявляється на етапі експлуатації виробів, тому оперують поняттям “експлуатаційна надійність”.
Для визначення окремих властивостей виробів уживають терміни “стан”, “граничний стан”. Стандарт регламентує 25 різновидів станів об’єктів. Розглянемо лише шість станів, зокрема справний, несправний, працездатний, непрацездатний, критичний, які характеризують машини та обладнання харчової, мікробіологічної і фармацевтичної промисловості.
Справний стан (справність) – стан об’єкта, за яким він здатний виконувати усі задані функції.
Несправний стан (несправність) – стан об’єкта, за яким він
нездатний виконувати хоча б одну із покладених на нього функцій.
Працездатний стан (працездатність) – стан об’єкта, який характеризується його здатністю виконувати усі потрібні функції.
Непрацездатний стан (непрацездатність) – стан об’єкта, за яким він нездатний виконувати хоча б одну з потрібних функцій.
Критичний стан – стан об’єкта, що може призвести до травмування людей, значних матеріальних збитків чи інших небажаних наслідків.
Граничний стан – стан об’єкта, за яким його подальша експлуатація неприпустима чи недоцільна або відновлення його непрацездатного стану неможливе чи недоцільне (гранично спрацьовані всі базові вузли і деталі).
Кожну з п’яти властивостей (безвідмовність, довговічність, ремонтопридатність, збережуваність, готовність) об’єкта, які характеризують його надійність, оцінюють відповідними показниками.
Безвідмовність об’єкта оцінюють такими показниками: імовірністю безвідмовної роботи (ІБР); середнім наробітком до відмови; інтенсивністю відмов; гамма-відсотковим наробітком на відмову; наробітком на відмову; параметром потоку відмов.
Імовірність безвідмовної роботи об’єкта (його вузлів і агрегатів) – це імовірність того, що протягом заданого наробітку відмова об’єкта не виникне.
Середній наробіток до відмови – це математичне сподівання наробітку об’єкта до першої відмови.
Інтенсивність відмов – умовна густина імовірності виникнення відмови об’єкта, яка визначається за умови, що до цього моменту відмова не виникла.
Гамма-відсотковий наробіток на відмову – це наробіток, протягом якого відмова об’єкта не виникне з імовірністю g, вираженою у відсотках.
Наробіток на відмову – це відношення наробітку ремонтопридатного об’єкта до математичного сподівання кількості його відмов протягом цього наробітку.
Параметр потоку відмов – це відношення математичного сподівання числа відмов відновлюваного об’єкта за досить малий його наробіток до значення цього наробітку.
Довговічність об’єкта оцінюють такими показниками: середнім ресурсом; середнім терміном служби; гамма-відсотковим ресурсом; гамма-відсотковим терміном служби; призначеним ресурсом; призначеним терміном служби.
Середній ресурс – це математичне сподівання ресурсу (від початку експлуатації або від моменту капітального ремонту об’єкта до настання його граничного стану).
Середній термін служби – це математичне сподівання терміну служби (календарної тривалості від початку експлуатації нового або відремонтованого об’єкта до настання його граничного стану).
Гамма-відсотковий ресурс – це сумарний наробіток, протягом якого об’єкт не досягне граничного стану із імовірністю g, вираженою у відсотках.
Гамма-відсотковий термін служби – це календарна тривалість експлуатації, протягом якої об’єкт не досягне граничного стану із імовірністю g, вираженою у відсотках.
Призначений ресурс – це сумарний наробіток, при досягненні якого експлуатацію об’єкта належить припинити незалежно від його технічного стану.
Призначений термін служби – це календарна тривалість експлуатації, при досягненні якої експлуатацію об’єкта належить припинити незалежно від його технічного стану.
Ремонтопридатність об’єкта оцінюють такими показниками: імовірністю відновлення; середньою тривалістю відновлення; гамма-відсотковою тривалістю відновлення; інтенсивністю відновлення; середньою інтенсивністю відновлення; середньою трудомісткістю ТО (ремонту).
Імовірність відновлення – це імовірність того, що час відновлення працездатного стану об’єкта не перевищить заданого значення.
Середня тривалість відновлення – це математичне сподівання часу відновлення працездатного стану об’єкта після відмови.
Гамма-відсоткова тривалість відновлення – це інтервал часу, протягом відновлення працездатності об’єкта здійснюється з імовірністю g, вираженою у відсотках.
Інтенсивність відновлення – це умовна густина імовірності відновлення працездатності об’єкта, визначена для одного моменту часу за умови, що до цього моменту відновлення не завершилося.
Середня інтенсивність відновлення – це її середнє значення в заданому інтервалі часу.
Середня трудомісткість ТО (ремонту) – це математичне сподівання трудомісткості ТО (ремонту), виражене у людино-годинах.
Збережуваність об’єкта оцінюють середнім терміном збережуваності і гамма-відсотковим терміном збережуваності.
Середній термін збережуваності – це математичне сподівання строку збережуваності.
Гамма-відсотковий термін збережуваності – це термін збережуваності, якого досягає об’єкт із заданою імовірністю g, вираженою у відсотках.
Готовність оцінюють такими показниками: коефіцієнтом готовності; коефіцієнтом неготовності; середнім коефіцієнтом готовності; стаціонарним коефіцієнтом готовності; коефіцієнтом оперативної готовності; коефіцієнтом технічного використання; коефіцієнтом збереження ефективності.
Коефіцієнт готовності – імовірність того, що об’єкт виявиться працездатним у довільний момент часу, крім запланованих періодів, протягом яких використання об’єкта за призначенням не передбачене.
Коефіцієнт неготовності (коефіцієнт простою) – імовірність того, що об’єкт виявиться непрацездатним у довільний момент часу, крім запланованих періодів, протягом яких використання об’єкта за призначенням не передбачене.
Середній коефіцієнт готовності – середнє значення нестаціонарного коефіцієнта готовності у заданому інтервалі часу.
Стаціонарний коефіцієнт готовності – значення коефіцієнта готовності, визначене для умов роботи об’єкта, коли середній параметр потоку відмов і середня тривалість відновлення залишаються сталими.
Коефіцієнт оперативної готовності – імовірність того, що за винятком тих запланованих періодів, протягом яких використання об’єкта за призначенням не передбачено, він у довільний момент часу виявиться у працездатному стані і надалі виконуватиме потрібну функцію протягом заданого інтервалу часу.
Коефіцієнт технічного використання – це відношення математичного сподівання сумарного часу перебування об’єкта у працездатному стані за деякий період експлуатації до математичного сподівання сумарного часу перебування об’єкта в працездатному стані та у простоях, зумовлених ТО і ремонтом за той самий період.
Коефіцієнт збереження ефективності – це відношення значення показника ефективності використання об’єкта за призначенням за певну тривалість експлуатації до номінального значення цього показника, розрахованого за умови, що відмови цього об’єкта протягом того ж періоду не виникають.
Кожен із цих показників, які характеризують ту чи іншу властивість об’єкта щодо його надійності, розраховують за результатами попередньо проведених експериментальних досліджень чи спостережень з використанням відповідних формул.
Таблиця 9.2
Групові та індивідуальні показники надійності
| Групи виро-бу | Вид виробу | Вид показника | Безвідмовність | Довго-вічність | Ремонто-здатність | Збережливість | Комплексні показники |
| І | Групові | - | Тр (Тсл) або Трγ (Тсл γ) | Тв (Рв/t) або Sто(Sр) | Тс(Тс γ) Тсн | Кеф | |
| Індивідуальні | Тру (Тслу) або Трн (Тслн) | ||||||
| групові | - | Показники довговічності основних складових частин | |||||
| індивідуальні | |||||||
| ІІ | Відновлювальні | групові | То або w(t) | Тр (Тсл) або Трγ (Тсл γ) | |||
| індивідуальна | Тру (Тслу) або Ррн (Тслн) | ||||||
| Невідновлювальні | групові | Тел або L(t) абоР(t) | |||||
| індивідуальна | Ту | ||||||
| групові | Показники надійності основних складових частин | ||||||
| індивідуальні |
Порядок виконання
1. Проаналізувати функціональне призначення, обґрунтувати та вибрати групові та індивідуальні показники надійності.
2. Обрати виріб і для нього дати визначення обраних показників надійності і розрахувати їх, користуючись таблицями 9.1, 9.2.
3. З вибраних показників надійності вказати ті, які найбільш важливі для оцінки працездатності виробу.
9.4. Контрольні запитання
1) Які показники безвідмовності найбільш важливі при аналізі роботи технічних об’єктів.
2) Які вироби відносять до І групи.
3) Дайте визначення коефіцієнту технічного використання. Як впливають на нього показники ремонтопридатності.
4) Як пов’язані надійність і довговічність з робото знатністю технічних об’єктів.
5) Назвіть основні чинники, що впливають на надійність виробів.
10. Практична робота. Оцінка результатів спостережень відмов виробів та визначення закону їх розподілу
10.1. Завдання.Для напрацювання до руйнування колінчастого вала, поданого у вигляді випадкових величин (табл. 10.1) оцінити результати спостережень та визначити закон їх розподілу.
10.2. Теоретичні відомості про закони розподілу випадкових величин
При випробуваннях нових зразків техніки найбільш достовірну інформацію про надійність її роботи для спостереження та фіксації відмов (порушення працездатності), їх статистичне оброблення та аналіз причин їх виникнення. Зафіксовані відмови, як правило, непередбачувані та мають вигляд випадкових величин. Ймовірнісні методи їх дослідження розвиваються з використанням теоретичних розподілів випадкових величин, які часто називають законами теорії надійності. Розглянемо найбільш уживані теоретичні розподіли.
10.2.1. Нормальний розподіл
Одним із найбільш універсальних, зручних і широко застосовуваних для практичних розрахунків законів розподілу випадкових величин є закон розподілу Гаусса (рис.10.1). Універсальність цього закону полягає в тому, що його вважають граничним законом, з якого випливають інші (Релея, Вейбулла, Пуассона, біноміальний тощо).
Нормальний розподіл проявляється тоді, коли зміна випадкової величини зумовлена багатьма причинами рівнозначного впливу. Йому підпорядковуються напрацювання до відмови і на відмову більшості відновлюваних і невідновлюваних виробів, які спрацьовуються і кородують, похибки вимірювань тощо.
Функцію щільності розподілу розраховують за формулою
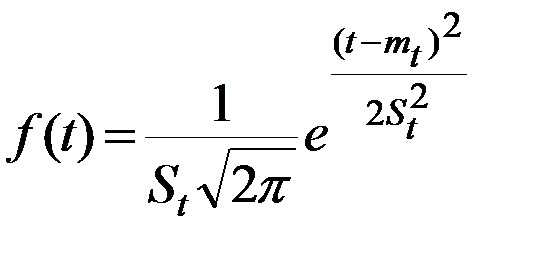 (10.1)
(10.1)
Цей розподіл має два незалежних параметри: математичне сподівання mt і середнє квадратичне відхилення S. Значення цих параметрів оцінюють за такими формулами:
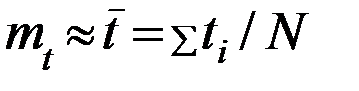 ; (10.2)
; (10.2)
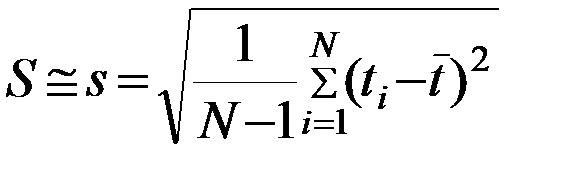 , (10.3)
, (10.3)
де 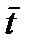 ,
, 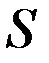 – статистичні оцінки відповідно математичного сподівання і середнього квадратичного відхилення (наприклад, часу напрацювання об‘єкта до відмови або на відмову).
– статистичні оцінки відповідно математичного сподівання і середнього квадратичного відхилення (наприклад, часу напрацювання об‘єкта до відмови або на відмову).
Математичне сподівання в цьому законі розподілу визначає положення центра кривої на осі абсцис, а середнє квадратичне відхилення – ширину фігури, описаної цією кривою (рис. 10.1). При деякому напрацювання  імовірність відмови Q(t)=F(t) наближається до 1,0, а імовірність безвідмовної роботи P(t) падає до нуля (рис. 10.1).
імовірність відмови Q(t)=F(t) наближається до 1,0, а імовірність безвідмовної роботи P(t) падає до нуля (рис. 10.1).
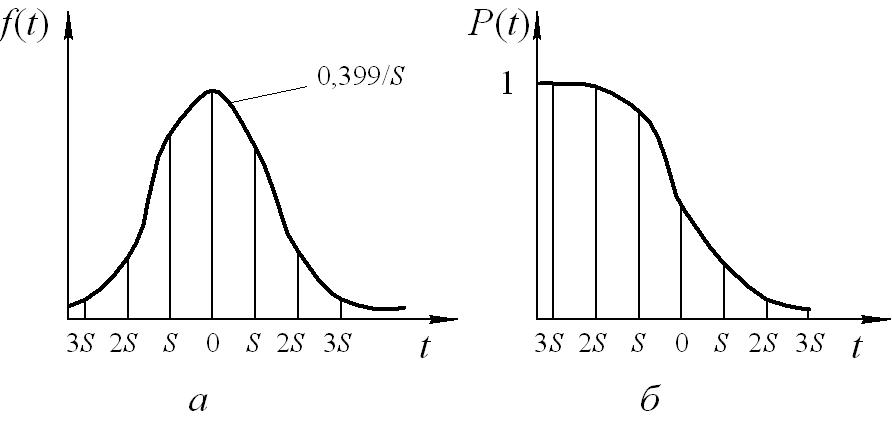
Рис.10.1.Щільність ймовірності (а) та інтегральна функція
імовірності (б) нормального розподілу
Крива щільності розподілу випадкової величини тим гостріша і вища, чим менше значення S (рис. 10.2).
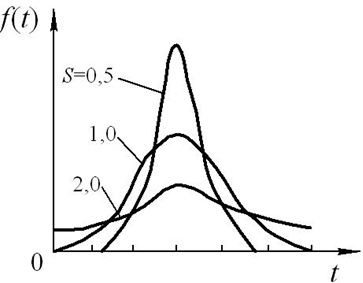
Рис.10.2. Щільність імовірності f(t) при нормальному розподілу
10.2.2. Логарифмічно нормальний розподіл
Розподіл випадкової величини набуває характеру логарифмічно нормального, коли за нормальним законом змінюється логарифм цієї величини. Цим законом описується напрацювання до відмови більшості деталей, особливо якщо відмови настають через втомлюваність і старіння (наприклад, підшипників кочення).
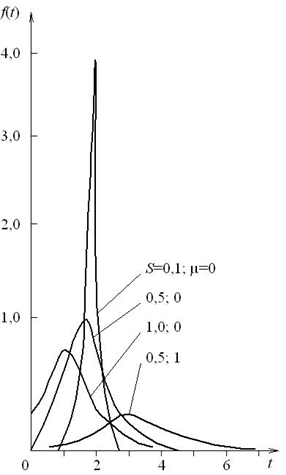
Рис. 10.3. Щільність імовірності f(t) логарифмічно нормального розподілу
Щільність розподілу (рис. 10.3) описується такою залежністю:
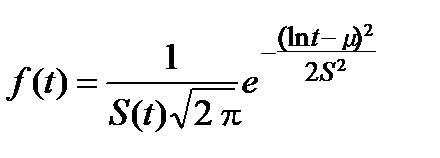 (10.4)
(10.4)
де μ, S - параметри, які оцінюють за результатами спостережень чи випробувань.
Так, якщо випробовують N виробів до відмови, то 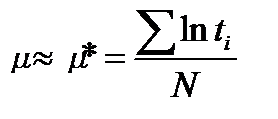 ;
;
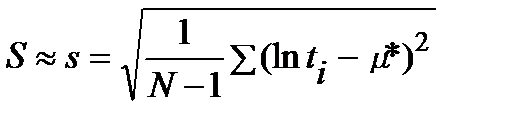 , (10.5)
, (10.5)
де μ*, s – статистична оцінка параметрів μ та s.
Імовірність безвідмовної роботи P(t) визначають залежно від значень квантилів
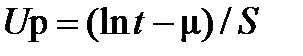 . (10.6)
. (10.6)
10.2.3. Експоненційний розподіл
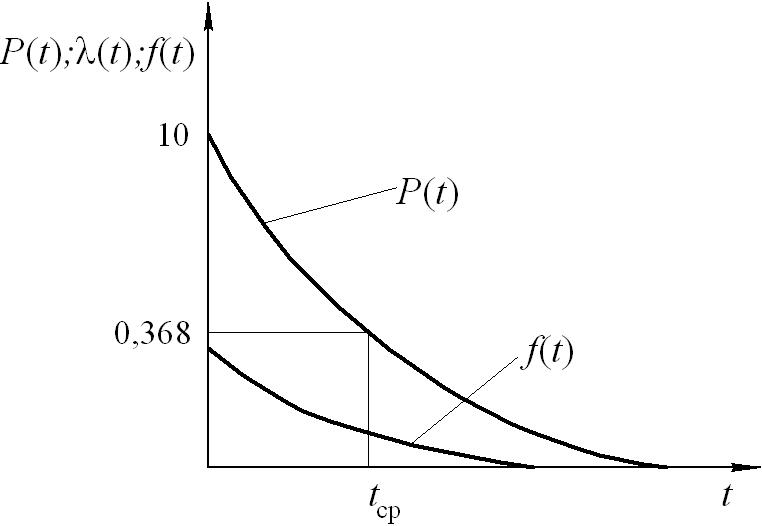
Для експоненційного закону (рис. 10.4) сталою величиною є інтенсивність відмов, тобто
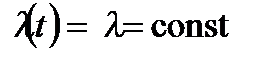 ; (10.7)
; (10.7)
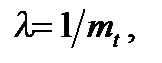 (10.8)
(10.8)
де 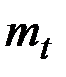 - математичне сподівання напрацювання до відмови, що визначається на підставі оброблення результатів спостережень чи випробувань:
- математичне сподівання напрацювання до відмови, що визначається на підставі оброблення результатів спостережень чи випробувань:
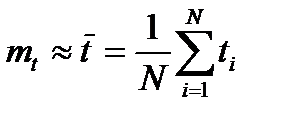 , (10.9)
, (10.9)
де 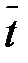 ─ середнє значення напрацювання;
─ середнє значення напрацювання; 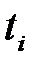 ─ поточне значення напрацювання.
─ поточне значення напрацювання.
Якщо напрацювання виразити в годинах, то 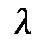 виразиться кількістю відмов за годину.
виразиться кількістю відмов за годину.
|
| Рис. 10.4. Характеристики експоненційного розподілу |
10.2.4. Розподіл Вейбулла
Цей розподіл характеризується такими функціями (рис. 10.5):
- ймовірністю безвідмовної роботи
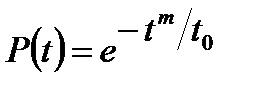 ; (10.10)
; (10.10)
- інтенсивністю відмов
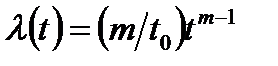 ; (10.11)
; (10.11)
густиною розподілу
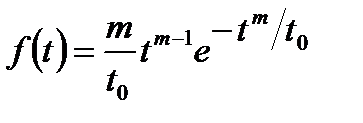 . (10.12)
. (10.12)
Розподіл Вейбулла також має два параметри: параметр форми m > 0 і масштабний параметр t0 > 0.
Математичне сподівання і середнє квадратичне відхилення визначають відповідно так:
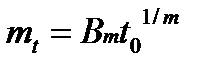 ;
; 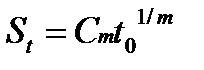 (10.13)
(10.13)
де 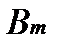 і
і 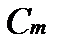 - коефіцієнти (див. табл. 4.2).
- коефіцієнти (див. табл. 4.2).
Якщо протягом певного часу 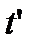 відмови не відбуваються, то імовірність безвідмовної роботи визначають за формулою
відмови не відбуваються, то імовірність безвідмовної роботи визначають за формулою
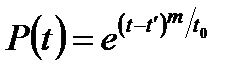 .
.
Іноді характеристики розподілу Вейбулла записують з використанням інших позначень. Наприклад, імовірність безвідмовної роботи можна подати так: 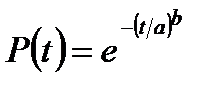
де 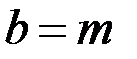 і
і 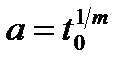
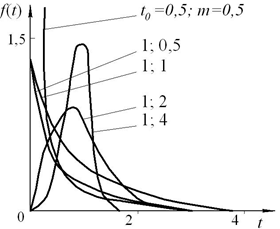
Рис. 10.5. Щільність розподілу ( 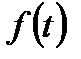 ) при розподілі Вейбулла.
) при розподілі Вейбулла.
Розподіл Вейбулла задовільно описує напрацювання до відмови підшипників та інших деталей машин, які руйнуються від утоми. Його застосовують також для оцінювання надійності вузлів підіймально-транспортних машин і механізмів.
Порядок виконання
1. Відповідно до варіанту з додатку 10, табл.. Д.10.1 (за номером в списку академічної групи) побудувати варіаційний ряд випадкових величин напрацювань, розбити його на 10 інтервалів, встановити границі інтервалів, розрахувати показники надійності, побудувати гістограму емпіричного розподілення.
2. На підставі розрахованих даних побудувати гістограму.
3. Визначити час експлуатації виробу до першого технічного огляду.
Приклад виконання
Визначити кількісні характеристики функції P(t), F(t), f(t) колінчастого вала холодильного компресора при випробуваннях його на втому по заданому варіаційному ряду напрацювання до руйнування (табл. 10.1).
Таблиця 10.1
Границі інтервалів напрацювань колінчастих валів холодильних компресорів до відмови, * год
| [1…5) | [5…9) | [9…13) | [13…17) | [17…21) |
| 1,0 | 5,1 6,1 | 9,0 9,5 10,0 11,0 12, 0 | 13,0 16, 5 | 17, 0 |
| 1,5 | 5,2 6,3 | 9,1 9,5 10,1 11,1 12,1 | 13,5 16,6 | 17,5 |
| 2,0 | 5,3 6,5 | 9,1 9,6 10,2 11,2 12,2 | 14,0 | 18,0 |
| 2,5 | 5,4 6,7 | 9,2 9,6 10,3 11,3 12,3 | 14,5 | 18,5 |
| 3,0 | 5,5 7,0 | 9,2 9,7 10,4 11,4 12,4 | 15,0 | 19,0 |
| 3,5 | 5,6 7,1 | 9,3 9,8 10,5 11,5 12,5 | 15,5 | 19,5 |
| 4,0 | 5,7 7,2 | 9,3 9,9 10,6 11,6 12,6 | 16,0 | 20,0 |
| 4,5 | 5,8 7,5 | 9,4 9,9 10,7 11,7 12,7 | 16,5 | 20,5 |
| 4,8 | 5,9 8,0 | 9,4 9,9 10,8 11,8 12,8 | 16,5 | |
| 4,9 | 6,0 8,9 | 9,4 9,9 10,9 11,9 12,9 | 16,5 | |
| *N=(ti+ti+1)/2 – кількість випробуваних колінчастих валів |
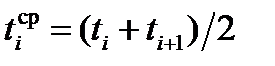 – середнє напрацювання вала в інтервалі напрацювання;
– середнє напрацювання вала в інтервалі напрацювання;
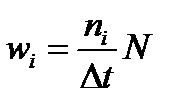 – частість настання відмови;
– частість настання відмови;
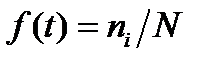 – щільність розподілу випадкової величини;
– щільність розподілу випадкової величини;
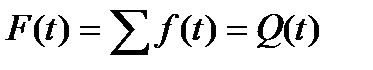 – імовірність відмови колінчастого вала;
– імовірність відмови колінчастого вала;
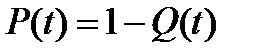 – імовірність безвідмовної роботи вала.
– імовірність безвідмовної роботи вала.
Результати розрахунку показників надійності занесені до табл. 10.2.
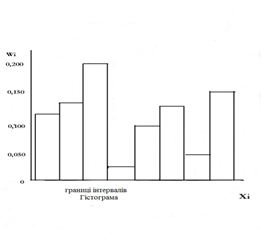
Емпіричне розподілення подаємо у вигляді гістограми.
При побудові гістограми над кожним відрізком абсцис, відповідних інтервалу, будується прямокутник, площа якого пропорційна частоті або частості. При однаковій ширині інтервалів частоті або частості пропорційна висота прямокутників.
Таблиця 10.2
Результати розрахунку показників надійності
| Номер інтервалу | 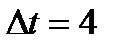
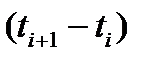
| 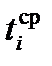
| 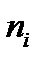
| 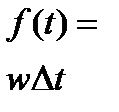
| 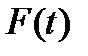
| 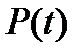
|
| 1…5 | 0,100 | 0,10 | 0,90 | |||
| 5…9 | 0,200 | 0,30 | 0,70 | |||
| 9…13 | 0,500 | 0,80 | 0,20 | |||
| 13…17 | 0,120 | 0,92 | 0,08 | |||
| 17…21 | 0,080 | 1,00 | 0,00 |
При великій кількості інтервалів плавна крива, що описує їх границі наближається до кривої закону розподілу.
10.4. Контрольні запитання.
1) Що таке гістограма? Як і з якою метою її будують?
2) Назвіть основні характеристики законів розподілу випадкових величин.
3) Як пов’язані між собою щільність розподілу відмов і безвідмовність виробів?
4) Які області застосування функцій частоти відмов 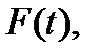 інтенсивності відмов
інтенсивності відмов 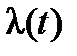 і параметра потоку відмов
і параметра потоку відмов 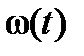 у теорії надійності?
у теорії надійності?
5) У яких випадках моделі відмов описуються ймовірнісними законами надійності (нормальним, логарифмічно нормальним, гамма, Пуассона, Вейбулла, експоненційним)?
11. Практична робота. Математичне визначення показників законів розподілу відмов
11.1. Завдання.Для визначеного за даними в практичному занятті 10 закону розподілу розрахувати математичні характеристики і побудувати графічні залежності 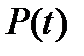 ,
, 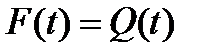 ,
, 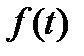 .
.
11.2. Теоретичні відомості про математичні показники надійності
11.2.1. Математичне сподівання (середнє значення) 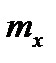 – основна і найпростіша характеристика випадкової величини X. Значення математичного сподівання, що визначається за результатами спостережень, для дискретних і безперервних величин називають оцінкою математичного сподівання, або оцінкою середнього значення
– основна і найпростіша характеристика випадкової величини X. Значення математичного сподівання, що визначається за результатами спостережень, для дискретних і безперервних величин називають оцінкою математичного сподівання, або оцінкою середнього значення 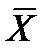 :
:
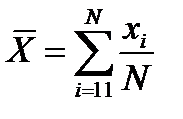 , або
, або 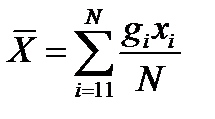 ,
,
де хі – поточне значення випадкової величини; gi – кількість однакових значень хі; N – загальна кількість спостережень.
У першій формулі складають усі N членів, у другій – кількість членів з різними значеннями хі. За досить великої кількості спостережень вважають, що mx = 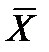 . В імовірнісних задачах математичне сподівання визначають залежно від щільності розподілу f(x) (для безперервних величин) або ймовірності pі появи значення хі (для дискретних величин):
. В імовірнісних задачах математичне сподівання визначають залежно від щільності розподілу f(x) (для безперервних величин) або ймовірності pі появи значення хі (для дискретних величин):
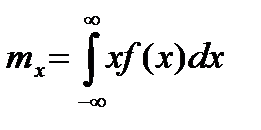 ;
; 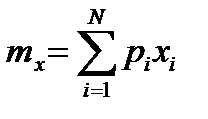 .
.
11.2.2. Мода – значення випадкової величини, що трапляється найчастіше, або найбільш імовірне її значення.
11.2.3. Квантиль– значення випадкової величини, що відповідає заданій імовірності. Квантиль, що відповідає імовірності 0,5, називають медіаною.
11.2.4. Медіанає центром групування випадкової величини. Площу під графіком медіана поділяє навпіл.
Для нормального закону розподілу випадкових величин, який описує відома крива Гаусса, математичне сподівання, мода і медіана збігаються.
11.2.5. Дисперсія випадкової величини – це математичне сподівання квадрату відхилення цієї величини від її математичного сподівання.
Оцінка дисперсії випадкової величини – середнє значення квадрата різниці між значеннями випадкової величини та її середнім значенням:
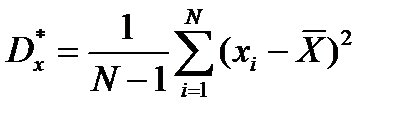 , або
, або 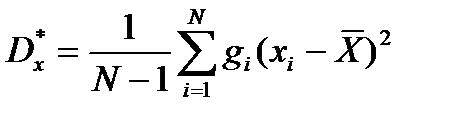 ,
,
де N – загальна кількість спостережень; хі – поточне значення випадкової величини; 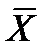 – середнє значення випадкової величини; gi – кількість однакових значень випадкової величини.
– середнє значення випадкової величини; gi – кількість однакових значень випадкової величини.
Поняття “дисперсія ” означає розсіювання і характеризує розбіжність випадкової величини.
Для безперервних випадкових величин
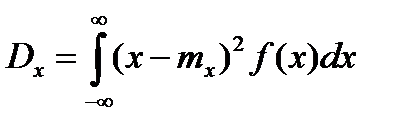 .
.
Для дискретних випадкових величин
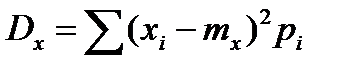 ,
,
де pі – імовірність появи значення 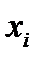 .
.
Дисперсія вимірюється квадратом розмірності випадкової величини. Оскільки зручніше користуватися характеристикою розсіювання, що має розмірність випадкової величини, введено характеристику середнє квадратичне відхилення, тобто квадратний корінь з дисперсії:
Дата добавления: 2016-03-15; просмотров: 1199;
