Буксование ведущих колес на подъеме

Условие буксования ведущих колес определяется схемой привода автомобиля. Рассмотрим последовательно все возможные варианты:

1. Автомобиль классической компоновки с задними ведущими и передними ведомыми колесами.

Условие буксования ведущих колес на подъеме определяется так:

R_z2 * φ_x

Пренебрегаем в расчетах силой сопротивления воздуха и силой инерции, так как очевидно, что при преодолении максимально возможного подъема автомобиль движется с малой скоростью и равномерно.

Тогда баланс проекций сил на плоскость дороги имеет вид:

R_x2 = R_x1 + G_a * Sin ά

где ά – угол подъема;

Учитывая, что R_x1 = R_z1 * f

Где f – коэффициент сопротивления качению ведомых колес

Получим баланс сил в следующем виде:

R_z2 * φ_x = R_z1 * f + G_a * Sin ά

Определим значения нормальных реакций на осях автомобиля ( см. раздел 2.4)

G_a

: R_z1 = ------* ( L₂* Cos ά - h_g * Sin ά )

L

G_a

R_z2 = ----* ( L₁* Cos ά + h_g * Sin ά )

L

Подставим полученные выражения нормальных реакций на осях автомобиля в уравнение баланса сил и после преобразования решим полученное уравнение относительно угла подъема, на котором будет иметь место буксование задних ведущих колес автомобиля с классической компоновкой:

φ_x* L₁ – f* L₂

ά_букс1 = Arc tg ----------------------

L - h_g*( φ_x+ f)

В многих учебниках по теории автомобиля обычно приводится несколько иная формула, характеризующая угол подъема, на котором происходит буксование ведущих колес автомобиля с классической компоновкой:

φ_x* L₁

ά_букс1 = Arc tg ----------------------

L - h_g* φ_x

Эта формула получена при условии пренебрежения силой сопротивления качению колес передней оси. Она достаточно справедлива для случая преодоления подъема на дороге с хорошим твердым покрытием, однако при преодолении подъема на дороге с относительно большим коэффициентом сопротивления качению использование этой формулы может привести к значительным погрешностям.

2. Переднеприводный автомобиль.

У переднеприводного автомобиля уравнение баланса проекций сил на плоскость дороги имеет вид:

R_x1 = R_x2 + G_a * Sin ά

Соответственно, значения касательных реакций на колесах мостов имеют вид: R_x1 = R_z1 * φ_x ; R_x2 = R_z2 * f

Значения нормальных реакций на колесах переднего и заднего мостов переднеприводного автомобиля имеют такой же вид, как и для автомобиля с классической компоновкой.

Подставим полученные выражения нормальных реакций на осях автомобиля в уравнение баланса сил и после преобразования решим полученное уравнение относительно угла подъема, на котором будет иметь место буксование задних ведущих колес переднеприводного автомобиля:

φ_x* L₂ – f* L₁

ά_букс2 = Arc tg ----------------------

L + h_g*( φ_x+ f)

Аналогично, приближенная формула, полученная с пренебрежением силой сопротивления задних ведомых колес, имеет вид:

φ_x* L₁

ά_букс2 = Arc tg ----------------------

L - h_g* φ_x

3. Полноприводный автомобиль с незаблокированным межосевым дифференциалом.

Считаем, что на автомобиле установлен несимметричный межосевой дифференциал, характеризующийся коэффициентом распределения моментов К_д,, характеризующим и распределение касательных реакций по м ОСТам автомобиля:

R_x2

К _д = ------

R_x1

Поскольку при движении на подъем нормальная нагрузка на передних колесах уменьшается в сравнении со статической, есть все основания предположить, что буксовать на подъеме начнут колеса передней оси. В этом случае касательная реакция на передних колесах будет равна:

R_x1 = R_z1* φ_x

Соответственно, на задних колесах будет реализована касательная реакция R_x2, увеличенная в сравнении с реакцией на передних колесах в К_д раз:

R_x2 = R_z1* φ_x* К _д

Уравнение баланса сил в этом случае имеет вид:

R_x1 + R_x2 = G_a * Sin ά

Подставив в уравнение баланса сил значения касательных реакций, выраженных через нормальные реакции и решив полученное уравнение относительно угла подъема, на котором будут буксовать передние колеса полноприводного автомобиля с незаблокированным межосевым дифференциалом , получим:

φ_x* L₂*(1+К _д)

ά_букс3 = Arc tg -------------------

L + h_g* φ_x(1+ К _д)

4. Полноприводный автомобиль с блокированным приводом мостов

У полноприводного автомобиля с блокированным приводом мостов

уравнение баланса проекций сил на плоскость дороги имеет вид:

R_x1 +R_x2 =G_a * Sin ά

Значения касательных реакций при полном использовании сцепных свойств определяются следующим образом:

R_x1 = R_z1* φ_x

R_x2 = R_z2 * φ_x

Подставляя значения касательных реакций колес мостов в уравнение баланса сил и проведя преобразования , получим:

ά_букс4 = Arc tg φ_x

Во избежание опрокидывания при движении полноприводного автомобиля на подъеме должно быть выдержано условие:

.

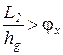Это же условие справедливо и для заднеприводного автомобиля. Переднеприводный автомобиль не может преодолевать подъем, на котором возможно его опрокидывание