Дифференциал c повышенным внутренним трением
Если учесть трение в дифференциале, то мощность, подведенная к дифференциалу разделяется на три потока:
P0=Р`+P``+Pr.
Т.к P0= Т0 · ω0; P`= Т`· ω`; P``= Т``· ω``.
Здесь:
P0 - мощность, подведенная к чашке дифференциала;
Р` -- мощность, снимаемая с забегающей полуоси;
P``- мощность, снимаемая с отстающей полуоси;
Pr – мощность внутреннего трения в дифференциале;
Т0 – момент, подведенный к чашке дифференциала;
Т`· - момент, снимаемый с забегающей полуоси;
Т``· - момент, снимаемый с отстающей полуоси;
ω0 – частота вращения чашки дифференциала;
ω` - частота вращения забегающей полуоси;
ω``- частота вращения отстающей полуоси.
Мощность внутреннего трения представляет собой произведение момента внутреннего трения Тr на разницу частот вращения полуосей:
Pr= Тr · (ω`– ω``).
Мощностной баланс дифференциала примет вид:
Т0 · ω0= Т`· ω` + Т``· ω`` + Тr · (ω`– ω``)
Кинематическим свойством дифференциала является связь частот в механизме: 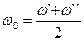 .
.
Силовым свойством дифференциала является связь моментов
T0 = Т` + Т``
Тогда выразим момент на второй полуоси через подведенный момент и момент на первом колесе:
Т``= Т0 – Т`
и подставим это значение в мощностной баланс дифференциала:
Т0 · ω0= Т`· ω` + (Т0 – Т`)· ω`` + Тr · (ω`– ω``).
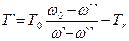 .
.
Учитывая 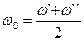 окончательно получим:
окончательно получим:
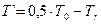
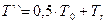 .
.
Дата добавления: 2016-03-15; просмотров: 802;
