Задание №4 Площадь сферы
| Полукруг вращается вокруг своего диаметра. Диаметр равен 7м. Вычисли площадь поверхности тела вращения? | |
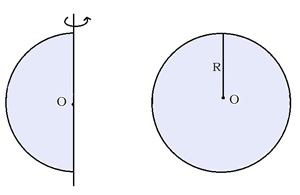
| Дано:Полукруг вращается вокруг диаметра . D=7м Найти: S сферы -? |
Решение:
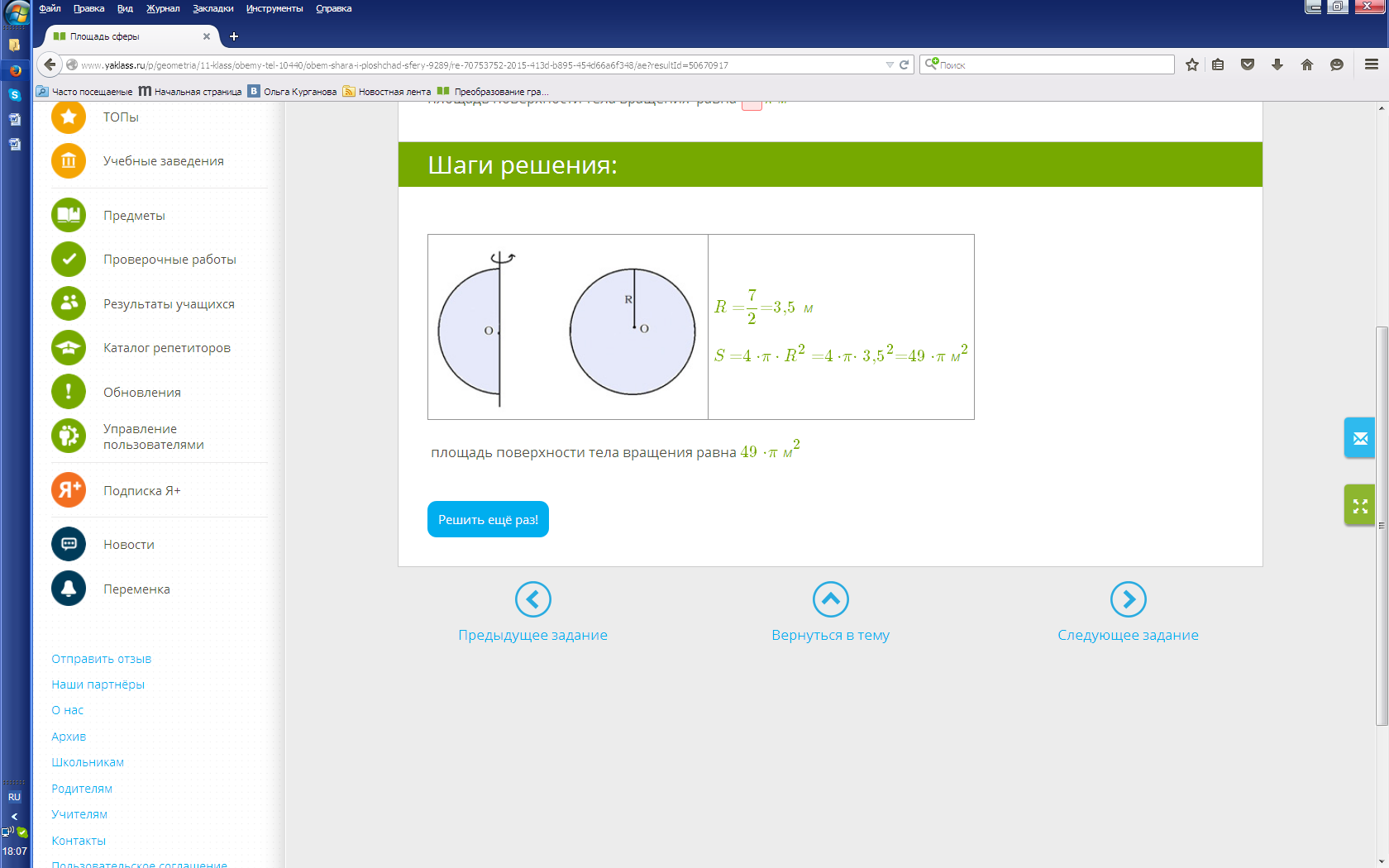 Ответ: S сферы =49π м2
Ответ: S сферы =49π м2
| |
| Решить задание на ЯКласс | №4 Площадь сферы |
Задание №5 Шар касается плоскости
| Шар с центром в точке O касается плоскости в точке A. Точка B лежит в плоскости касания. Найди объём шара, если AB=10,5см , а BO=14,5см. | |
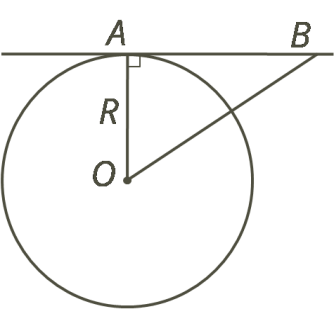
| Дано:Шар касается плоскости в точке А . АВ=10.5см ВО=14.5см Найти: Vшара-? |
Решение:
Радиус шара AO, проведённый в точку касания, перпендикулярен касательной плоскости.
Вычислим AO, используя теорему Пифагора.
AO2=BO2−AB2=14,52−10,52=100⇒R=AO=10см
V(шара)=  ⋅π⋅R3= ⋅π⋅R3=  ⋅π⋅103= ⋅π⋅103= 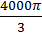 см3
Ответ: Vшара= см3
Ответ: Vшара= 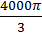 см3 см3
| |
| Решить задание на ЯКласс | № 5 Шар касается плоскости |
Содержание отчета
Записать конспект и решение заданий в тетрадь, ответить на контрольные вопросы
Контрольные вопросы
| По какой формуле вычисляется объем и площадь поверхности шара? | |
| Если шар вписан в куб, у которого известно ребро, то чему будет равен радиус шара? | |
| По какой формуле вычисляется объем шарового сегмента? | |
| Если в шар вписан цилиндр, то может ли высота цилиндра быть больше диаметра шара? |
12
Дата добавления: 2016-03-15; просмотров: 9115;
