Объем наклонной призмы, конуса и пирамиды

1. Дидактическое оснащение практического занятия:

Теория по ссылке: Объём наклонной призмы, пирамиды и конуса

Определение наклонной призмы

Наклонная призма — это призма, боковые рёбра которой не перпендикулярны основанию. ∠KAF=α — угол между боковым ребром и плоскостью основания. KF=h — высота наклонной призмы ( перпендикуляр, проведённый из какой-нибудь точки одного основания к плоскости другого основания ).Часто перпендикуляр проводят с одной из вершин верхнего основания.

Площадь боковой и полной поверхности наклонной призмы

Площадью боковой поверхности наклонной призмы называется сумма площадей её боковых граней. Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра. Площадью полной поверхности наклонной призмы называется сумма площадей всех её граней. Перпендикулярное сечение — пересечение призмы и плоскости, перпендикулярной её боковому ребру.

Объем наклонной призмы

Объём наклонной призмы равен произведению площади основания на высоту V=S(ABCD)⋅h

Многогранник, одна грань которого является n-угольником, а остальные грани — треугольники с общей вершиной, называется пирамидой, n-угольник называется основанием пирамиды, а треугольники — боковыми гранями. Перпендикуляр, проведённый из вершины пирамиды к плоскости основания, называется высотой пирамиды.

Углы пирамиды

Углы, которые образованы боковой гранью и основанием пирамиды, называются двугранными углами при основании пирамиды. Угол, который образован двумя боковыми гранями, называется двугранным углом при боковом ребре пирамиды. Угол, который образован двумя боковыми рёбрами одной грани пирамиды, называется углом при вершине пирамиды. На рисунке ∢DSC.

Основные формулы пирамиды

Площадь боковой поверхности равна сумме площадей всех боковых граней пирамиды: S=S1+S2+S3+... Некоторые формулы годятся только для определённых видов пирамиды. Площадь полной поверхности Sп.п.=S+Sоснования Объём пирамиды V=

Sоснования H, где H — высота пирамиды. Формула объёма используется для пирамид любого вида.

Усеченная пирамида

Усечённой пирамидой называется часть пирамиды между её основанием и плоскостью, параллельной ему. Объём усечённой пирамиды V=

H⋅(S1+

+S2), Где S1иS2− площади оснований

Апофема усеченной пирамиды это перпендикуляр, проведенный к основаниям усеченной пирамиды Площадь боковой поверхности правильной усечённой пирамиды Sбок.=

(P1+P2)⋅h, гдеP1иP2−периметры оснований, h - апофема правильной усечённой пирамиды, на данных рисунках это отрезок LF.

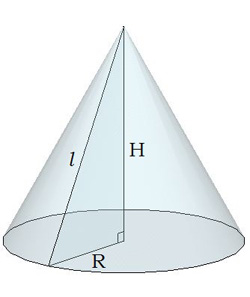Объем и площадь поверхности конуса

Площадь боковой поверхности конусавычисляется по формуле: S(бок.)=πRl где R - радиус конуса, l - образующая конуса. Площадь основания конуса вычисляется по формуле S(полн.) = S(бок.) + S(круга) S(круга) =πR² Площадь полной поверхности конуса вычисляется по формуле S(полн.) = S(бок.) + S(круга) = πRl+πR² Объём конуса вычисляют по формуле V =

⋅H⋅ S(круга) = πR²⋅

Площадью боковой поверхности конуса является площадь ее развёртки. Развёрткой боковой поверхности конуса является круговой сектор.

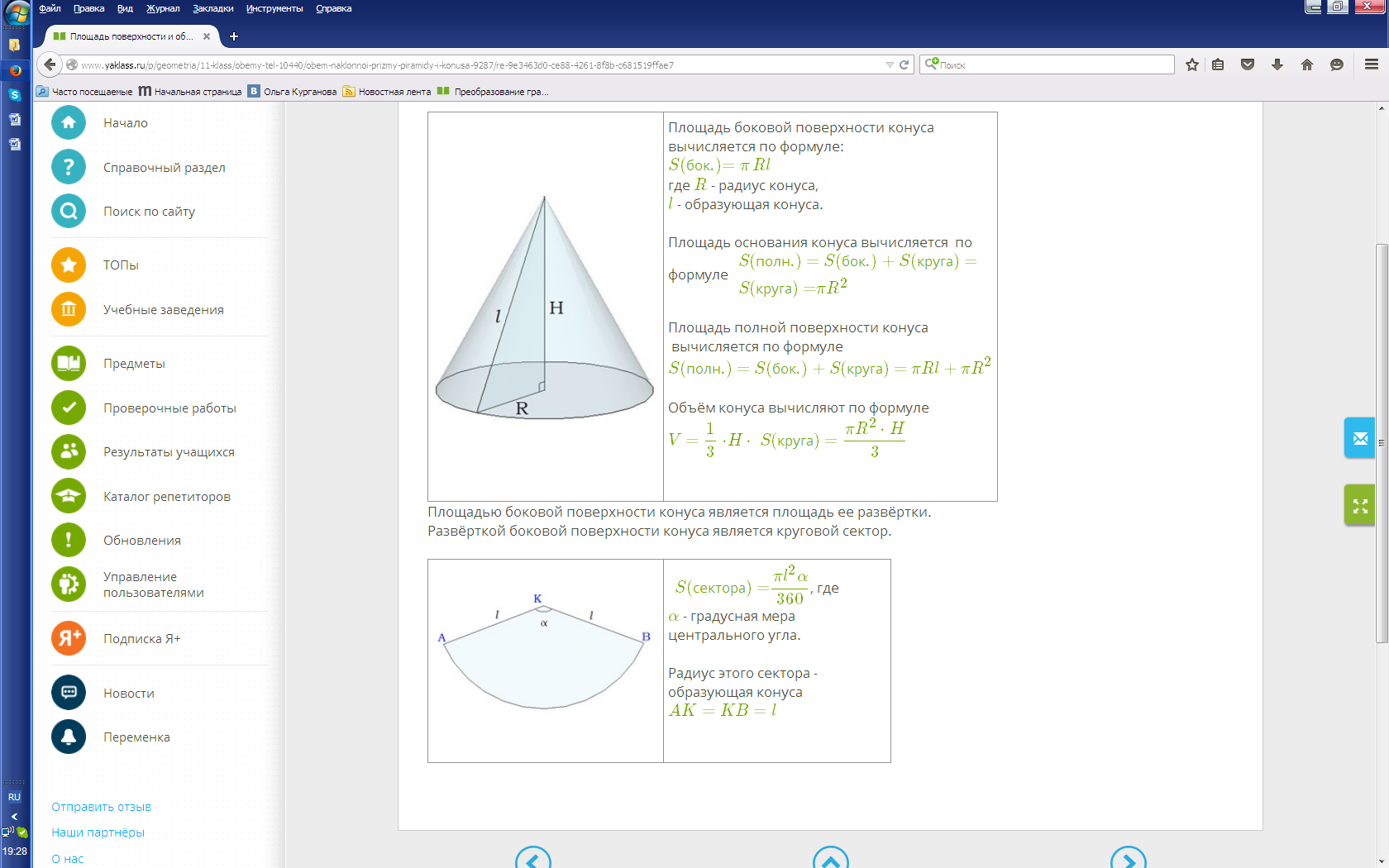
Усеченный конус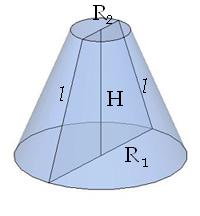

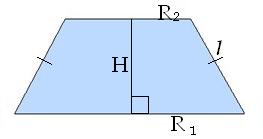
Усечённый конус - тело вращения, которое получается при вращении прямоугольной трапеции вокруг меньшей боковой стороны.

R2 - радиус меньшего основания R1 - радиус большего основания l - образующая H – высота

Площадь боковой поверхности усечённого конуса

Sбок.=π⋅l⋅(R1+R2),г

деR1иR2−радиусы оснований, l - образующая.

Sполн.=Sбок.+S1+S2,

гдеS1,S2 - площади оснований усечённого конуса.

Объём усечённого конуса
V= π⋅H⋅(R²1+R1⋅R2+R²2),

где H - высота усечённого конуса.

При решении задач чаще всего достаточно нарисовать только осевое сечение усечённого конуса, которое является равнобедренной трапецией.

Задания

Задание№1. Объём конуса и цилиндра

Цилиндр и конус имеют общее основание и общую высоту. Вычисли объём конуса, если объём цилиндра равен 12,39.
	Дано: Цилиндр и конус имеют общее основание и высоту V_{цилиндра}=12.39 Найти: V_конуса-?
Решение: Объём цилиндра можно вычислить по формуле V(цилиндра)=π⋅R²⋅H. Объём конуса можно вычислить по формуле V(конуса)=π⋅R²⋅ Соответственно, V(конуса)= = =4,13 Ответ: V(конуса)= 4,13
Решить задание на ЯКласс	№1 Объём конуса и цилиндра

Задание №2 Объём треугольной пирамиды по формуле

Высота треугольной пирамиды равна 13 см, а площадь основания равна 39 см². Вычислите объем пирамиды.
	Дано: H_{пирамиды}=13см S_{основания}=39см² Найти: V_{пирамиды}-?
Решение: Формула объема пирамиды: V= Sосн.⋅H V= 39⋅13=169 см3 Объем пирамиды равен 169 см³ Ответ: V(пирамиды)= 169 см³
Решить задание на ЯКласс	№2 Объём треугольной пирамиды по формуле

Дата добавления: 2016-03-15; просмотров: 5201;