Функции сложного процента, используемые в базовых инвестиционных расчетах
Функциями сложного процента, используемыми в базовых инвестиционных расчетах, являются:
1. Накопление денежной единицы (единичного вклада) S
2. Текущая стоимость денежной единицы ν
3. Текущая стоимость аннуитета α
4. Взнос на амортизацию денежной единицы РМТ
5. Будущая стоимость аннуитета Sα (накопление периодической денежной единицы)
6. Фактор фонда возмещения SFF
Все формулы функций сложного процента приведены для денежного вклада размером в одну денежную единицу, годовой ставки накопления, начисления процентов по вкладу один раз в год.
2.1. Накопление единичного вклада показывает будущую стоимость S одной денежной единицы, размещенной на условиях сложного депозита на t лет под i процентов годовых.
|
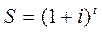 (2.1)
(2.1)
|
 |
Рис 2.1. Схема накопления стоимости единичного вклада
Определим будущую стоимость первоначального вклада в 100 ден ед, размещенного на 5 лет под 20% с использованием функции сложного процента: S= (1+0,2)5 * 100 = 2,48832 * 100 = 248,832
Табл. 2.1 - Определение будущей величины депозитного вклада и размера процентного дохода, при различных схемах начисления процентов
| Год | Накопление на счету осуществляется по схеме | ||||||
| Сложного процента | Простого процента | ||||||
| % | депозит | % | депозит | ||||
| 28,8 | 172,8 | ||||||
| 34,56 | 207,36 | ||||||
| 41,47 | 248,832 | ||||||
| итого | 248,832 | ||||||
2.2 Текущая стоимость денежной единицы ν показывает сегодняшний эквивалент стоимости денежного вклада, который мы ожидаем к получению через t лет, если сегодняшняя ставка сложного процента і.
Процесс определения сегодняшнего (текущего) эквивалента будущего денежного потока также называют дисконтированием, а коэффициент приведения – коэффициентом дисконтирования
Формула коэффициента дисконтирования 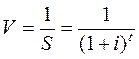 (2.2)
(2.2)

Рис 2.2 Схема определения текущей стоимости будущего денежного потока
Пример: Определить текущую стоимость будущего поступления в размере 248,832 ден ед, ожидаемого к получению через 5 лет, если сегодняшняя ставка по сложным банковским депозитам составляет 20%. Сегодняшний эквивалент будущего вклада рассчитаем с использованием коэффициента дисконтирования: 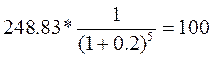
Т.е. ожидаемый к получению через пять лет депозит в размере 248,832 ден ед сегодня эквивалентен 100 ден ед.
2.3. Текущая стоимость обычного аннуитета α.
Аннуитетом называется серия одинаковых по величине платежей, которые поступают через равномерные интервалы времени, в один и тот же момент. Различают аннуитеты:
- Обычный (единичный, постнумерандо) - серия одинаковых платежей., поступающих в конце периодов
- Авансовый (нулевой, преднумерандо) – серия одинаковых платежей, поступающих в начале периодов.
Текущая стоимость аннуитета показывает сегодняшнее значение эквивалента накопленной суммы одинаковых платежей, поступающих периодически в течение периода t , если ставка депозита i.
 | |||
 | |||
Рис. 2.3 Схема определения текущей стоимости аннуитета
Формула коэффициента аннуитета: 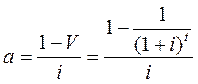 (2.3)
(2.3)
Таблица 2.2 - Определение текущей стоимости вклада в 1 ден ед, поступающего единично V, или периодически a
| год | V | a |
| 0.9091 | 0.9091 | |
| 0.8264 | 1.73551 | |
| 0.7513 | 2.4868 | |
| 0.6830 | 3.1698 |
2.4. Взнос на амортизацию денежной единицы РМТ показывает размер регулярного периодического платежа, поступающего t лет на погашение кредита, приносящего процентный доход i. Из этого взноса погашается и основная сумма кредита и проценты за его использование. Формула коэффициента
 |
Рис.2.4. Схема определения взноса на погашение (амортизацию) долга
Пример: Рассчитать взнос на погашение кредита в размере 3,1698 ден ед, если мы должны вернуть его за 4 года под 10% годовых. Платежи на погашение долга должны поступать равномерно и периодически. Размер единичного платежа на погашение долга рассчитаем по формуле: 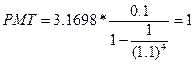 . График погашения долга представим в таблице 2.3.
. График погашения долга представим в таблице 2.3.
Таблица 2.3- График погашения кредита
| год | Остаток долга на начало года | Платеж РМТ | Выплата на погашение процентов i | Выплата на погашение основной суммы долга | Остаток долга на конец года |
| 4= i *2 | 5=3-4 | 6=2-5 | |||
| 3.1698 | 0.3169 | 0.68302 | 2.4868 | ||
| 2.4868 | 0.2487 | 0.75132 | 1.7355 | ||
| 1.7355 | 0.1735 | 0.8265 | 0.9090 | ||
| 0.9090 | 0.0909 | 0.9090 | - |
Таким образом, регулярно внося 1 ден ед в конце каждого года, мы сумеем погасить за 4 года и основную сумму кредита 3,1698 ден ед и 10% за его использование
2.5 Будущая стоимость аннуитета Sα позволяет узнать чему будет равна в конце ожидаемого периода t стоимость серии одинаковых взносов, депонированных под i процентов в конце каждого интервала поступления. Формула коэффициента будущей стоимости аннуитета:
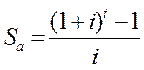 (2.5)
(2.5)
Пример: рассчитаем будущую (накопленную) стоимость аннуитета в 1 ден единицу, поступающего в течение 3 лет на 10% депозит. Накопленный остаток на нашем депозите к концу 3 года составит : 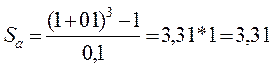
 |
Рис. 2.5. Образование будущей стоимости единичного аннуитета
 | |||||||
 |  | ||||||
 | |||||||
Движение денежных вкладов в 1 ден ед , регулярно и равномерно поступающих 3 года на 10% процентный депозитный счет, продемонстрируем в форме таблицы 2.4.
Таблица 2.4-Накопление средств на депозите
| год | Поступление на депозит | Начисление процентов за текущий год | Остаток депозита на конец текущего года |
| 1,00 | 0,00 | 1,00 | |
| 1,00 | 0,10 | 2,10 | |
| 1,00 | 0,21 | 3,31 |
2.6.фактор фонда возмещения SFF показывает, чему должен быть равен размер регулярного периодического платежа, поступающего t лет на сложный депозит под i процентов, с целью образования известной суммы к концу периода. Формула коэффициента фонда возмещения:
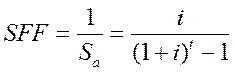 (2.6)
(2.6)

Рис.2.6 Схема поступления платежей на возмещение конечной суммы
Движение денежных вкладов в 1 ден ед , регулярно и равномерно поступающих 3 года на 10% процентный депозитный счет, продемонстрируем в форме таблицы 2.4.
Таблица 2.4-Накопление средств на депозите
| год | Поступление на депозит | Начисление процентов за текущий год | Остаток депозита на конец текущего года |
| 1,00 | 0,00 | 1,00 | |
| 1,00 | 0,10 | 2,10 | |
| 1,00 | 0,21 | 3,31 |
Все формулы финансовой математики представлены для случая, если начисления процентов и поступления на вклад осуществляются 1 раз в году. Если же частота накопления и начисления должна быть больше чем один раз в год, все формулы трансформируются одинаковым образом: ставка процента i делится на частоту накопления σ, а период накопления t, выраженный в годах, умножается на частоту накопления σ.
Вопросы для контроля знаний по теме:
1. Типы протекания инвестиционного процесса
2. Изменение ценности денег во времени, его влияние на инвестиции
3. Функции денежной единицы, их формулы и графики
Литература к теме:
1. Григорьев В.В., Федотова М.А. Оценка предприятия: теория и практика. – М.: ИНФРА-М, 1997.
2.Кочович Е. Финансовая математика: теория и практика финансово-банковских расчетов. – М.: Финансы и статистика, 1994
Дата добавления: 2016-03-15; просмотров: 1103;
