Газовые законы. Идеальный и реальный газы
Иногда для изучения газовых систем достаточно знать только макроскопические параметры, характеризующие состояние всей системы. Такими параметрами для описания газовой системы, находящейся в тепловом равновесии, являются объем системы, ее масса, давление и температура. Равновесным состоянием системы называют такое состояние, при котором все ее макроскопические параметры сколь угодно долго остаются неизменными, при этом давление и температура имеют одинаковые значения во всех частях объема.
Исторически впервые установление связей между равновесными макроскопическими параметрами газовых систем произведено опытным путем. Экспериментальные газовые законы формулируются следующим образом:
1. Для данной массы газа при постоянной температуре 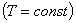 давление газа изменяется обратно пропорционально объему (закон Бойля-Мариотта): давление газа изменяется обратно пропорционально объему (закон Бойля-Мариотта):
В соответствии с формулой (5) изотермический процесс представляется на графике гиперболой, которая называется изотермой (рис.3). | 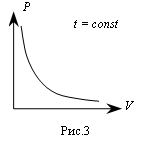
|
2. Для данной массы газа при постоянном давлении 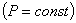 объем газа изменяется линейно с температурой (закон Гей-Люссака):
объем газа изменяется линейно с температурой (закон Гей-Люссака):
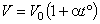 , ,
| (6) |
где  - объем газа при 0oС, V - объем газа при температуре
- объем газа при 0oС, V - объем газа при температуре 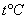 ,
, 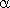 - коэффициент объемного расширения газа.
- коэффициент объемного расширения газа.
3. Для данной массы газа при постоянном объеме 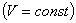 давление газа изменяется линейно с температурой (закон Шарля):
давление газа изменяется линейно с температурой (закон Шарля):
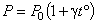 , ,
| (7) |
где 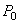 - давление газа при 0oС, P - давление газа при температуре
- давление газа при 0oС, P - давление газа при температуре 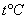 ,
,  - термический коэффициент давления газа.
- термический коэффициент давления газа.
Оказалось, что для всех газов
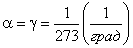 .
.
Согласно формулам (6) и (7), изобарический и изохорический процессы представляются на графиках прямыми линиями (изобарами и изохорами), проходящими наклонно к оси температур и пересекающими ее в точке 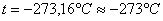 (рис.4, 5).
(рис.4, 5).
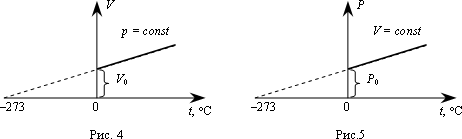
Точка 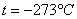 принята за начало отсчета (нуль) новой шкалы температур, называемой термодинамической шкалой или шкалой Кельвина, или абсолютной шкалой. Температура, отсчитываемая по этой шкале, называется термодинамической; нуль этой шкалы называется нулем Кельвина.
принята за начало отсчета (нуль) новой шкалы температур, называемой термодинамической шкалой или шкалой Кельвина, или абсолютной шкалой. Температура, отсчитываемая по этой шкале, называется термодинамической; нуль этой шкалы называется нулем Кельвина.
Если цену деления термодинамической шкалы сохранить той же, что и на шкале Цельсия, то температура Т будет связана с температурой t, измеряемой по шкале Цельсия, формулой
 , ,
| (8) |
при этом 0 К = -273oС.
Из формулы (4) следует, что при температуре, равной 0 К,
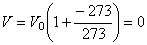 , ,
|
то есть при температуре 0 К вещество исчезает. Этот явно неверный вывод говорит о том, что экспериментальные газовые законы неприменимы в области низких температур. При низких температурах, как будет показано далее, вещество не может существовать в газообразном состоянии: оно переходит в жидкое или даже твердое состояние.
Нуль шкалы Кельвина - самая низкая из возможных температур вещества, при 0 К полностью прекращается хаотическое движение молекул в веществе. Однако это не значит, что в нем прекращается всякое движение. Сохраняется, например, движение электронов в атоме. В настоящее время удается охлаждать малые объемы вещества до температуры, близкой к 0 К, не достигая последнего лишь на несколько тысячных долей Кельвина.
С помощью термодинамической температуры закон Гей-Люссака можно записать в более простом виде:
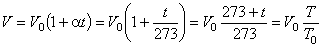 ,
,
где 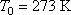 соответствует 0oС. Следовательно,
соответствует 0oС. Следовательно,
 . .
| (9) |
При постоянном давлении объем газа пропорционален термодинамической температуре.
Предложите учащимся самим аналогичным образом преобразовать формулу (7) и получить
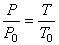 . .
| (10) |
Формулы (9) и (10) представляют собой математическое выражение газовых законов Гей-Люссака и Шарля.
Закон Дальтона. Пусть в некотором объеме находится смесь газов (например, воздух), имеющая давление P. Удалим из объема все газы, кроме одного (например, азота). Тогда он займет весь объем и будет иметь давление P1, называемое парциальным давлением первого газа.
Парциальным давлением газа, входящего в газовую смесь, называется давление, которое имел бы этот газ, если бы он один занимал весь объем, предоставленный смеси. Аналогично введем парциальные давления для других газов, входящих с смесь P2, P3 и т.д.
Для смеси газов справедлив закон Дальтона: давление газовой смеси равно сумме парциальных давлений, входящих в нее газов.
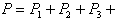 ... ...
| (11) |
Закон Авогадро. На основании опытов с различными газами итальянский ученый А.Авогадро установил следующий закон:
При одинаковых температуре и давлении в равных объемах любого газа содержится одинаковое число молекул.
При нормальных условиях, то есть при давлении 1,0133·105 Па и температуре 273,16 К этот объем составляет 0,022414 м3/моль.
Закон Клапейрона. Закон установлен путем объединения законов Бойля-Мариотта, Гей-Люссака и Шарля и описывает процессы, при которых одновременно изменяются все три параметра 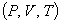 состояния газа:
состояния газа:
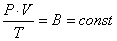 . .
| (12) |
Числовое значение постоянной В зависит от массы газа и его природы.
Уравнение Менделеева-Клапейрона. В 1875 г. Д.И. Менделеев, исходя из законов Клапейрона и Авогадро, получил наиболее общее выражение уравнения состояния газа, связывающее между собой объем V, давление P, температуру Т, массу m и молярную массуМ газа:
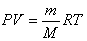 . .
| (13) |
Постоянная 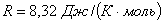 одинакова для всех газов и называется молярной газовой постоянной. Уравнение Менделеева-Клапейрона является также экспериментальным законом.
одинакова для всех газов и называется молярной газовой постоянной. Уравнение Менделеева-Клапейрона является также экспериментальным законом.
При выводе основного уравнения молекулярно-кинетической теории было показано, что макроскопический параметр Рсвязан со средней кинетической энергией поступательного движения молекул 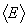 соотношением
соотношением
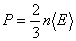 . .
| (14) |
Можно показать, что и другая макроскопическая характеристика состояния газа - термодинамическая температура - также зависит от этой энергии.
Для одного моля газа уравнение (13) перепишем следующим образом:
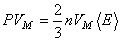 ,
, 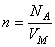 .
.
или
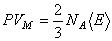 . .
| (15) |
Уравнение Менделеева-Клапейрона для одного моля газа запишется в виде:
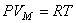 . .
| (16) |
Сопоставив (13) и (15), получаем
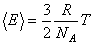 . .
| (17) |
Где 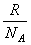 =k - постоянная Больцмана,
=k - постоянная Больцмана,  .
.
Тогда уравнение (17) примет вид:
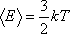 . .
| (18) |
Используя формулы (14) и (18), предложите учащимся получить выражение:
| P = nkT. | (19) |
Из этой формулы видно, что при одинаковых температуре и давлении все газы содержат в равных объемах одинаковое число молекул.
Предложите учащимся, используя формулу (19) подсчитать число молекул в 1 м3 газа при нормальных условиях. Еще раз напомним, что нормальные условия: 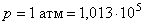 Па, Т = 273 К (0oС). Полученное число называется постоянной Лошмидта
Па, Т = 273 К (0oС). Полученное число называется постоянной Лошмидта 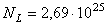 м-3.
м-3.
Уравнение Больцмана (18) имеет очень большое значение в молекулярной физике. Из него следует, что температура является мерой средней кинетической энергии поступательного движения молекул.
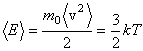 . .
| (20) |
Величина
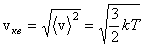 . .
| (21) |
называется средней квадратичной скоростью хаотического движения молекул.
Уравнение Больцмана получено для модели газа, состоящего из очень маленьких упругих твердых шариков (ближе всего к этой модели одноатомная молекула), находящихся в хаотическом движении и обладающих в трехмерном пространстве тремя степенями свободы. Тогда кинетическая энергия, приходящаяся на одну степень свободы молекулы, равна
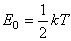 . .
| (22) |
При подсчете кинетической энергии молекулы, имеющей i степеней свободы, используется формула
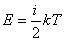 . .
| (23) |
Пример 1. Стенки сосуда, в котором находится газ температуры Т, имеют температуру Тст . В каком случае давление газа на стенки сосуда больше: когда стенки сосуда холоднее газа 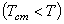 или когда теплее
или когда теплее 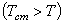 ?
?
Решение. Если температура стенок сосуда Тст совпадает с температурой газа Т, то молекула, ударяясь о стенку, меняет нормальную компоненту импульса 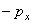 на
на 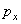 . Значит суммарное изменение импульса равно
. Значит суммарное изменение импульса равно 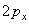 .
.
Когда температура стенок Тст больше температуры газа Т, газ нагревается. Это означает, что молекулы газа отскакивают от стенки с большей скоростью, чем налетают, а, следовательно, и с большим импульсом. В результате изменение импульса будет больше, чем 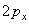 (рис.6).
(рис.6).
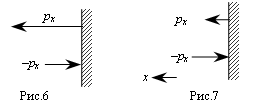
Если же 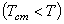 , то газ охлаждается, то есть молекулы газа отскакивают от стенки с меньшим импульсом, чем налетают на нее. Ясно, что изменение импульса в этом случае будет меньше, чем
, то газ охлаждается, то есть молекулы газа отскакивают от стенки с меньшим импульсом, чем налетают на нее. Ясно, что изменение импульса в этом случае будет меньше, чем 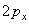 (рис.7). Так как в соответствии со вторым законом Ньютона изменение импульса пропорционально средней силе, то давление газа на стенки больше, когда стенки теплее газа
(рис.7). Так как в соответствии со вторым законом Ньютона изменение импульса пропорционально средней силе, то давление газа на стенки больше, когда стенки теплее газа 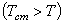 .
.
Пример 2. Определить среднеквадратичную скорость молекул 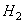 и
и 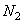 при нормальных условиях.
при нормальных условиях.
Решение. В этой задаче, несмотря на то, что молекулы являются двухатомными, мы применяем формулу
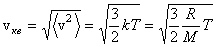 ,
,
учитывая только 3 поступательные степени свободы. Еще раз напомним, что нормальные условия - Т = 273 К (0oС),Р - 1 атмосфера. Решая в системе СИ, имеем: для водорода 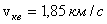 , для азота
, для азота 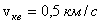 .
.
Реальные газы. Уравнение Менделеева-Клапейрона описывает поведение идеального газа, молекулы которого можно рассматривать как материальные точки, не взаимодействующие друг с другом. Молекулы реального газа имеют, как мы знаем, некоторый, хотя и очень малый, размер и связаны между собой силами взаимодействия, правда, тоже малыми. Однако при низкой температуре или высоком давлении, когда молекулы газа находятся близко друг от друга, пренебрегать их размерами и силами взаимодействия уже недопустимо.
В этих случаях уравнение состояния идеального газа оказывается весьма неточным. Чтобы получить уравнение состояния реального газа, голландский физик Ван-дер-Ваальс ввел в уравнение Менделеева-Клапейрона поправки на размер молекул и на действие сил взаимодействия между ними. В результате уравнение состояния одного моля реального газа приняло вид
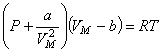 . .
| (24) |
Выражение (24) - уравнение Ван-дер-Ваальса. Здесь а и b - постоянные Ван-дер-Ваальса, для разных газов они имеют свои значения.
Если мы имеем дело не с одним, а с  молями газа объемом V, то в уравнении (24) следует сделать замену:
молями газа объемом V, то в уравнении (24) следует сделать замену:
 .
.
Поправка в первой скобке 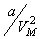 обусловлена силами притяжения между молекулами. Она имеет размерность давления, и ее часто называют внутренним давлением. На стенку сосуда такой газ оказывает давление Р. Однако, если бы силы притяжения между молекулами мгновенно исчезли, то давление на стенку сосуда стало бы
обусловлена силами притяжения между молекулами. Она имеет размерность давления, и ее часто называют внутренним давлением. На стенку сосуда такой газ оказывает давление Р. Однако, если бы силы притяжения между молекулами мгновенно исчезли, то давление на стенку сосуда стало бы 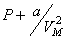 . То есть при переходе от идеального газа к реальному давление на стенку уменьшается из-за сил притяжения между молекулами.
. То есть при переходе от идеального газа к реальному давление на стенку уменьшается из-за сил притяжения между молекулами.
Поправка b связана с собственным объемом и ее размерность 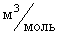 . При малых давлениях и высоких температурах
. При малых давлениях и высоких температурах 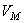 становится большим, поэтому
становится большим, поэтому 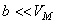 и
и 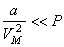 , то есть поправки в уравнение Ван-дер-Ваальса становятся пренебрежимо малыми, и оно превращается в уравнение Менделеева-Клапейрона. Вывод уравнения Ван-дер-Ваальса является упрощенным, но это уравнение дает возможность хотя бы качественно объяснить широкий круг явлений в газах и даже в жидкостях.
, то есть поправки в уравнение Ван-дер-Ваальса становятся пренебрежимо малыми, и оно превращается в уравнение Менделеева-Клапейрона. Вывод уравнения Ван-дер-Ваальса является упрощенным, но это уравнение дает возможность хотя бы качественно объяснить широкий круг явлений в газах и даже в жидкостях.
На рис.8 показаны три наиболее характерные изотермы (1,2,3), соответствующие уравнению (24) при температурах 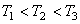 . При достаточно высокой температуре изотерма близка к изотерме идеального газа. Но при температуре
. При достаточно высокой температуре изотерма близка к изотерме идеального газа. Но при температуре 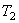 на изотерме появляется точка перегиба К. Точку К называют критической точкой. Соответствующие ей давление, температуру и изотерму называют также критическими.
на изотерме появляется точка перегиба К. Точку К называют критической точкой. Соответствующие ей давление, температуру и изотерму называют также критическими.
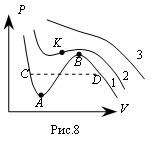
| Еще интересней ведет себя изотерма при температуре T1. Она содержит волнообразный участок САВD, между точкамиА и В которого наблюдается изотермическое уменьшение объема с уменьшением давления. Очевидно, что такого не может быть. Действительно, экспериментальный ход изотерм в этой области (изображен пунктирной прямой CD) говорит о том, что с изотермическим увеличением объема газа его давление на участкеCD не меняется. Опыт показывает, что на горизонтальном участке CD мы наблюдаем так называемый фазовый переход вещества из газообразного состояния в жидкое. Левее двухфазной области расположена область, соответствующая одной фазе - жидкости, правее - вещество находится в газообразном состоянии. |
Таким образом, изотермы, расположенные в области выше критической изотермы, описывают только газообразное состояние вещества. Чем выше температура Т3, тем ближе соответствующая изотерма к изотерме идеального газа.
Из таблицы 1, где приведены критические температура и давление некоторых веществ, видно, что, например, воздух в нормальных атмосферных условиях может существовать только в газообразном состоянии, а вода - как в жидком, так и газообразном состояниях.
Таблица 1
| Вещество | Ткр, К | Pкр, 105 Па | Вещество | Ткр, К | Pкр, 105 Па |
| Вода | Воздух (без СО2) | 38,5 | |||
| Аммиак | 112,3 | Азот | 33,4 | ||
| Углекислота | 72,7 | Водород | 13,2 | ||
| Кислород | 49,7 | Гелий | 2,3 |
Для более глубокого понимания отличия реального газа от идеального приведем пример.
Пример. Произведение давления газа на его объем не меняется с изменением объема при постоянной температуре, только если предположить, что газы, с которыми мы имеет дело, являются идеальными.
Определите, будет уменьшаться или увеличиваться произведение при очень сильном сжатии газа, если не делать предположения об идеальности последнего.
Решение. При очень сильном сжатии газа начинает сказываться отталкивание между молекулами - необходимо учитывать конечность их размеров. Это означает, что при всех прочих равных условиях давление реального газа тем больше, чем сильнее сжат газ. В результате, если при постоянной температуре произведение идеального газа постоянно, то для реального газа оно будет расти по мере уменьшения объема газа.
В XVII – XIX веках были сформулированы опытные законы идеальных газов. Кратко напомним их.
Изопроцессы идеального газа – процессы, при которых один из параметров остаётся неизменным.
1. Изохорический процесс. Закон Шарля. V = const.
Изохорическим процессом называется процесс, протекающий при постоянном объёме V. Поведение газа при этом изохорическом процессе подчиняется закону Шарля:
При постоянном объёме и неизменных значениях массы газа и его молярной массы, отношение давления газа к его абсолютной температуре остаётся постоянным: P/Т = const.
График изохорического процесса на РV-диаграмме называется изохорой. Полезно знать график изохорического процесса на РТ- и VT-диаграммах (рис. 1.6). Уравнение изохоры:
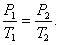
| (1.4.1) |

Рис. 1.6
Если температура газа выражена в градусах Цельсия, то уравнение изохорического процесса записывается в виде
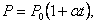
| (1.4.2) |
где Р0 – давление при 0 °С, α - температурный коэффициент давления газа равный 1/273 град-1. График такой зависимости на Рt-диаграмме имеет вид, показанный на рисунке 1.7.
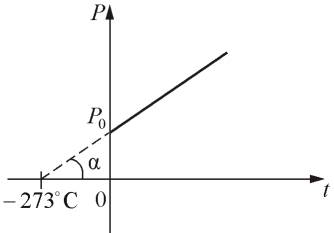
Рис. 1.7
2. Изобарический процесс. Закон Гей-Люссака. Р = const.
Изобарическим процессом называется процесс, протекающий при постоянном давлении Р. Поведение газа при изобарическом процессе подчиняется закону Гей-Люссака:
При постоянном давлении и неизменных значениях массы и газа и его молярной массы, отношение объёма газа к его абсолютной температуре остаётся постоянным: V/T = const.
График изобарического процесса на VT-диаграмме называется изобарой. Полезно знать графики изобарического процесса на РV- и РT-диаграммах (рис. 1.8).
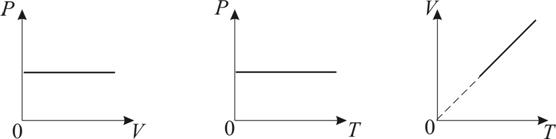
Рис. 1.8
Уравнение изобары:
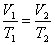 . .
| (1.4.3) |
Если температура газа выражена в градусах Цельсия, то уравнение изобарического процесса записывается в виде
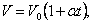
| (1.4.4) |
где α =1/273 град -1- температурный коэффициент объёмного расширения. График такой зависимости на Vt диаграмме имеет вид, показанный на рисунке 1.9.
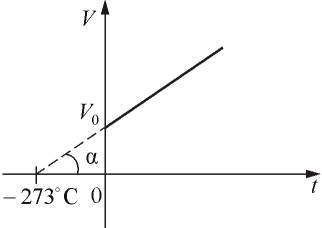
Рис. 1.9
3. Изотермический процесс. Закон Бойля – Мариотта. T = const.
Изотермическим процессом называется процесс, протекающий при постоянной температуре Т.
Поведение идеального газа при изотермическом процессе подчиняется закону Бойля – Мариотта:
При постоянной температуре и неизменных значениях массы газа и его молярной массы, произведение объёма газа на его давление остаётся постоянным: PV = const.
График изотермического процесса на РV-диаграмме называется изотермой. Полезно знать графики изотермического процесса на VT- и РT-диаграммах (рис. 1.10).
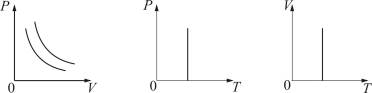
Рис. 1.10
Уравнение изотермы:
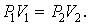
| (1.4.5) |
4. Адиабатический процесс (изоэнтропийный):
Адиабатический процесс – термодинамический процесс, происходящий без теплообмена с окружающей средой.
5. Политропический процесс. Процесс, при котором теплоёмкость газа остаётся постоянной. Политропический процесс – общий случай всех перечисленных выше процессов.
6. Закон Авогадро. При одинаковых давлениях и одинаковых температурах, в равных объёмах различных идеальных газов содержится одинаковое число молекул. В одном моле различных веществ содержится NA=6,02·1023молекул (число Авогадро).
7. Закон Дальтона. Давление смеси идеальных газов равно сумме парциальных давлений Р, входящих в неё газов:
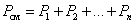
| (1.4.6) |
Парциальное давление Pn – давление, которое оказывал бы данный газ, если бы он один занимал весь объем.
При 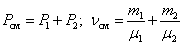 , давление смеси газов:
, давление смеси газов:

| (1.4.7) |
8. Объединённый газовый закон (Закон Клапейрона).
В соответствии с законами Бойля – Мариотта (1.4.5) и Гей-Люссака (1.4.3) можно сделать заключение, что для данной массы газа
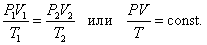
|
Дата добавления: 2016-03-15; просмотров: 2738;

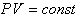 .
.