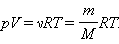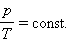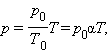Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы над внешними телами.
Первый закон термодинамики является обобщением опытных фактов. Согласно этому закону, энергия не может быть создана или уничтожена; она передается от одной системы к другой и превращается из одной формы в другую. Важным следствием первого закона термодинамики является утверждение о невозможности создания машины, способной совершать полезную работу без потребления энергии извне и без каких-либо изменений внутри самой машины. Такая гипотетическая машина получила название вечного двигателя (perpetuum mobile) первого рода. Многочисленные попытки создать такую машину неизменно заканчивались провалом. Любая машина может совершать положительную работу A над внешними телами только за счет получения некоторого количества теплоты Q от окружающих тел или уменьшения ΔU своей внутренней энергии.
Применим первый закон термодинамики к изопроцессам в газах.
1. Визохорном процессе (V = const) газ работы не совершает, A = 0. Следовательно,
|
2. Здесь U (T1) и U (T2) – внутренние энергии газа в начальном и конечном состояниях. Внутренняя энергия идеального газа зависит только от температуры (закон Джоуля). При изохорном нагревании тепло поглощается газом (Q > 0), и его внутренняя энергия увеличивается. При охлаждении тепло отдается внешним телам (Q < 0).
3. В изобарном процессе (p = const) работа, совершаемая газом, выражается соотношением
|
4. Первый закон термодинамики для изобарного процесса дает:
|
5. При изобарном расширении Q > 0 – тепло поглощается газом, и газ совершает положительную работу. При изобарном сжатии Q < 0 – тепло отдается внешним телам. В этом случае A < 0. Температура газа при изобарном сжатии уменьшается, T2 < T1; внутренняя энергия убывает, ΔU < 0.
6. В изотермическом процессе температура газа не изменяется, следовательно, не изменяется и внутренняя энергия газа,ΔU = 0.
Первый закон термодинамики для изотермического процесса выражается соотношением
|
Количество теплоты Q, полученной газом в процессе изотермического расширения, превращается в работу над внешними телами. При изотермическом сжатии работа внешних сил, произведенная над газом, превращается в тепло, которое передается окружающим телам.
Наряду с изохорным, изобарным и изотермическим процессами в термодинамике часто рассматриваются процессы, протекающие в отсутствие теплообмена с окружающими телами. Сосуды с теплонепроницаемыми стенками называютсяадиабатическими оболочками, а процессы расширения или сжатия газа в таких сосудах называются адиабатическими.


|
| Модель. Адиабатический процесс |
В адиабатическом процессеQ = 0; поэтому первый закон термодинамики принимает вид
|
т. е. газ совершает работу за счет убыли его внутренней энергии.
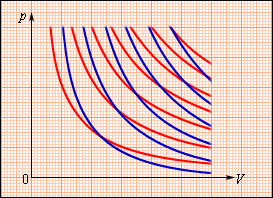
На плоскости (p, V) процесс адиабатического расширения (или сжатия) газа изображается кривой, которая называетсяадиабатой. При адиабатическом расширении газ совершает положительную работу (A > 0); поэтому его внутренняя энергия уменьшается (ΔU < 0). Это приводит к понижению температуры газа. Вследствие этого давление газа при адиабатическом расширении убывает быстрее, чем при изотермическом (рис. 3.9.2).
|
| Рисунок 3.9.2. Семейства изотерм (красные кривые) и адиабат (синие кривые) идеального газа |
В термодинамике выводится уравнение адиабатического процесса для идеального газа. В координатах (p, V) это уравнение имеет вид
|
Это соотношение называют уравнением Пуассона. Здесь γ = Cp / CV – показатель адиабаты, Cp и CV – теплоемкости газа в процессах с постоянным давлением и с постоянным объемом (см. §3.10). Для одноатомного газа 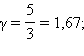 для двухатомного
для двухатомного 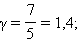 для многоатомного
для многоатомного 
Работа газа в адиабатическом процессе просто выражается через температуры T1 и T2 начального и конечного состояний:
|
Адиабатический процесс также можно отнести к изопроцессам. В термодинамике важную роль играет физическая величина, которая называется энтропией (см. §3.12). Изменение энтропии в каком-либо квазистатическом процессе равноприведенному теплу ΔQ / T, полученному системой. Поскольку на любом участке адиабатического процесса ΔQ = 0, энтропия в этом процессе остается неизменной.
Адиабатический процесс (так же, как и другие изопроцессы) является процессом квазистатическим. Все промежуточные состояния газа в этом процессе близки к состояниям термодинамического равновесия (см. §3.3). Любая точка на адиабате описывает равновесное состояние.
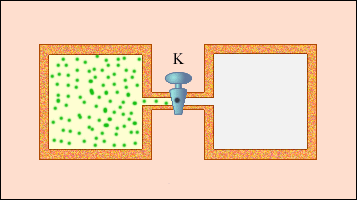
Не всякий процесс, проведенный в адиабатической оболочке, т. е. без теплообмена с окружающими телами, удовлетворяет этому условию. Примером неквазистатического процесса, в котором промежуточные состояния неравновесны, может служить расширение газа в пустоту. На рис. 3.9.3 изображена жесткая адиабатическая оболочка, состоящая из двух сообщающихся сосудов, разделенных вентилем K. В первоначальном состоянии газ заполняет один из сосудов, а в другом сосуде – вакуум. После открытия вентиля газ расширяется, заполняет оба сосуда, и устанавливается новое равновесное состояние. В этом процессе Q = 0, т.к. нет теплообмена с окружающими телами, и A = 0, т.к. оболочка недеформируема. Из первого закона термодинамики следует: ΔU = 0, т. е. внутренняя энергия газа осталась неизменной. Так как внутренняя энергия идеального газа зависит только от температуры, температура газа в начальном и конечном состояниях одинакова – точки на плоскости (p, V), изображающие эти состояния, лежат на одной изотерме. Все промежуточные состояния газа неравновесны и их нельзя изобразить на диаграмме.
Расширение газа в пустоту – пример необратимого процесса. Его нельзя провести в противоположном направлении.
|
| Рисунок 3.9.3. Расширение газа в пустоту |
Соотношение
| p = nkT, |
связывающее давление газа с его температурой и концентрацией молекул, получено в §3.2 для модели идеального газа, молекулы которого взаимодействуют между собой и со стенками сосуда только во время упругих столкновений. Это соотношение может быть записано в другой форме, устанавливающей связь между макроскопическими параметрами газа – объемом V, давлением p, температурой T и количеством вещества ν. Для этого нужно использовать равенства
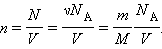
|
Здесь N – число молекул в сосуде, NА – постоянная Авогадро, m – масса газа в сосуде, M – молярная масса газа. В итоге получим:

|
Произведение постоянной Авогадро NА на постоянную Больцмана k называется универсальной газовой постоянной и обозначается буквой R. Ее численное значение в СИ есть:
| R = 8,31 Дж/моль·К. |
Соотношение
| (*) |
называется уравнением состояния идеального газа.
Для одного моля любого газа это соотношение принимает вид:
|
Если температура газа равна Tн = 273,15 К (0 °С), а давление pн = 1 атм = 1,013·105 Па, то говорят, что газ находится при нормальных условиях. Как следует из уравнения состояния идеального газа, один моль любого газа при нормальных условиях занимает один и тот же объем V0, равный
| V0 = 0,0224 м3/моль = 22,4 дм3/моль. |
Это утверждение называется законом Авогадро.
Для смеси невзаимодействующих газов уравнение состояния принимает вид
|
где ν1, ν2, ν3 и т. д. – количество вещества каждого из газов в смеси.
Уравнение, устанавливающее связь между давлением, объемом и температурой газа было получено в середине XIX века французским физиком Б. Клапейроном, в форме (*) оно было впервые записано Д. И. Менделеевым. Поэтому уравнение состояния газа называется уравнением Клапейрона–Менделеева.
Следует отметить, что задолго до того, как уравнение состояния идеального газа было теоретически получено на основе молекулярно-кинетической модели, закономерности поведения газов в различных условиях были хорошо изучены экспериментально. Поэтому уравнение (*) можно рассматривать как обобщение опытных фактов, которые находят объяснение в молекулярно-кинетической теории.
Газ может участвовать в различных тепловых процессах, при которых могут изменяться все параметры, описывающие его состояние (p, V и T). Если процесс протекает достаточно медленно, то в любой момент система близка к своему равновесному состоянию. Такие процессы называются квазистатическими. В привычном для нас масштабе времени эти процессы могут протекать и не очень медленно. Например, разрежения и сжатия газа в звуковой волне, происходящие сотни раз в секунду, можно рассматривать как квазистатический процесс. Квазистатические процессы могут быть изображены надиаграмме состояний (например, в координатах p, V) в виде некоторой траектории, каждая точка которой представляет равновесное состояние.
Интерес представляют процессы, в которых один из параметров (p, V или T) остается неизменным. Такие процессы называются изопроцессами.
Изотермический процесс (T = const)
Изотермическим процессом называют квазистатический процесс, протекающий при постоянной температуре T. Из уравнения (*) состояния идеального газа следует, что при постоянной температуре T и неизменном количестве вещества ν в сосуде произведение давления p газа на его объем V должно оставаться постоянным:
|

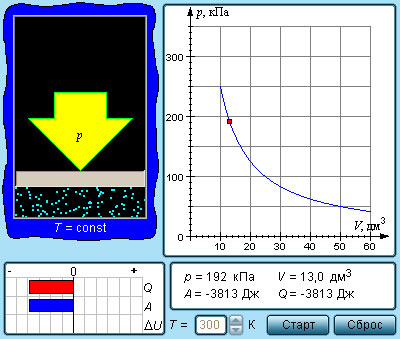
|
| Модель. Изотермический процесс |
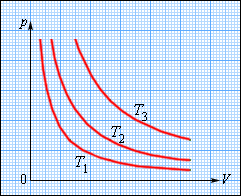
На плоскости (p, V) изотермические процессы изображаются при различных значениях температуры T семейством гиперболp ~ 1 / V, которые называются изотермами. Так как коэффициент пропорциональности в этом соотношении увеличивается с ростом температуры, изотермы, соответствующие более высоким значениям температуры, располагаются на графике выше изотерм, соответствующих меньшим значениям температуры (рис. 3.3.1). Уравнение изотермического процесса было получено из эксперимента английским физиком Р. Бойлем (1662 г.) и независимо французским физиком Э. Мариоттом(1676 г.). Поэтому это уравнение называют законом Бойля–Мариотта.
|
| Рисунок 3.3.1. Семейство изотерм на плоскости (p, V).T3 > T2 > T1 |
Изохорный процесс (V = const)
Изохорный процесс – это процесс квазистатического нагревания или охлаждения газа при постоянном объеме V и при условии, что количество вещества ν в сосуде остается неизменным.
Как следует из уравнения (*) состояния идеального газа, при этих условиях давление газа p изменяется прямо пропорционально его абсолютной температуре: p ~ T или
|


|
| Модель. Изохорный процесс |
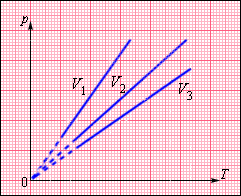
На плоскости (p, T) изохорные процессы для заданного количества вещества ν при различных значениях объема Vизображаются семейством прямых линий, которые называются изохорами. Большим значениям объема соответствуют изохоры с меньшим наклоном по отношению к оси температур (рис. 3.3.2).
|
| Рисунок 3.3.2. Семейство изохор на плоскости (p, T).V3 > V2 > V1 |
Экспериментально зависимость давления газа от температуры исследовал французский физик Ж. Шарль (1787 г.). Поэтому уравнение изохорного процесса называется законом Шарля.
Уравнение изохорного процесса может быть записано в виде:
|
где p0 – давление газа при T = T0 = 273,15 К (т. е. при температуре 0 °С). Коэффициент α, равный (1/273,15) К–1, называюттемпературным коэффициентом давления.
Изобарный процесс (p = const)
Изобарным процессом называют квазистатический процесс, протекающий при неизменным давлении p.
Уравнение изобарного процесса для некоторого неизменного количества вещества ν имеет вид:
|
где V0 – объем газа при температуре 0 °С. Коэффициент α равен (1/273,15) К–1. Его называют температурным коэффициентом объемного расширения газов.

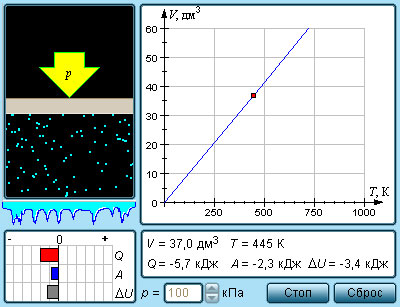
|
| Модель. Изобарный процесс |
На плоскости (V, T) изобарные процессы при разных значениях давления p изображаются семейством прямых линий (рис. 3.3.3), которые называются изобарами.

|
| Рисунок 3.3.3. Семейство изобар на плоскости (V, T).p3 > p2 > p1 |
Зависимость объема газа от температуры при неизменном давлении была экспериментально исследована французским физиком Ж. Гей-Люссаком (1862 г.). Поэтому уравнение изобарного процесса называют законом Гей-Люссака.
Экспериментально установленные законы Бойля–Мариотта, Шарля и Гей-Люссака находят объяснение в молекулярно-кинетической теории газов. Они являются следствием уравнения состояния идеального газа.
Дата добавления: 2016-03-15; просмотров: 2097;