Лекция №13 Өршіген беттің сәулеленуі.

Лекция жоспары:

· идеал жазық антеннаның бағыттылық сипаттамалары;

· қоздырылған беттің сәулелену өрісін анықтау;

· cәулелендіруші беттің бағыттылық диаграммасына өрістің әркелкі амплитудалық таралуының әсері.

13.1 Шеткі аймақтағы сәулеленетін бет өрісінің кернеулілігі. Идеал жазық антеннаның бағыттылық сипаттамалары

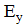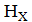Жіңішке бағыттылық диаграммасы сәулелеуші беті бар антеннаның көмегімен қалыптасуы мүмкін, яғни Е және Н перпендикуляр құраушы векторлары өзара үйлескен беткі қабат. Мұндай өршітуші бетті Гюйгенс элементар бастауының жиыны ретінде қарайды. dS кеңестігін құрайтын және өріс векторларының мәнін эквивалентті ток принципін негізге ала отырып, өзара перпендикуляр жоғарғы 2 токтың – электрлік және магниттік − ток өрістерінің суперпозициясы ретінде көрсетуге болады. Кеңістік көлемі аз болғандықтан, көрсетілген токтың жиынтығын − және токтары бар dy,dx ұзындықтағы өзара пенпендикуляр екі элементар диполь ретінде қарастыруға болады. Гюйгенс бастауының сәулеленуі элементар кеңістікке бағытталған. Е және Н жазықтықтарындағы бағыттылық сипаттамасы формуласы бойынша анықталады, ал БД кардиоид пішіндес болады. Сәулеленетін бет түріндегі антенналар сантиметрлі толқын диапазонында қолданылады (рупорлы антенналар, линзалы антенналар, шыны антенналар және т.б.)

Жалпы жағдайда, амплитуда сияқты өршітуші өріс фазасы да сәулеленетін беттің кординат нүктесінің функциясы бола алады, яғни:

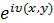= ƒ(x, y) = (13.1)

мұндағы: −тік бұрышты өршіген беттің нүктесіндегі өршітуші өрістің комплексті амплитудасы; – антенна центріндегі өршітуші өріс амплитудасы; ƒ(x, y) − өршітуші өріс амплитудасының координатқа тәуелділігін сипаттайтын функция (амплитудалық таралу); υ(x,y) – өршітуші өріс фазасының сәулеленетін беттің координат нүктесіне тәуелділігін анықтайтын функция (фазалық таралу). Кейбір жағдайларда амплитудалық және фазалық тарату тек қана бір координаттың функциясы болады.

Шеткі аймақтағы тік бұрышты сәулеленетін беттің әсерінен туындаған электрлік өріс кернеулігіне арналған формула табайық. Осы бетті ойша Гюйгенс бастауы бар dx және dy жақты элементар кеңістіктерге бөлеміз (сурет 13.1).

Өршіген беттің ең қарапайым жағдайын идеал сәулеленетін бет (идеал жазық антенна) жағдайын қарастырайық.

Идеал жазық антенна деп Е және Н векторларындағы әрбір нүктедегі тангенстік құраушылардың амплитуда мен фазасы бірдей бағытта болатын, яғни координатқа тәуелсіз болатын идеал өршіген бетті айтамыз. ƒ(x,y) =1, υ(x,y)=0 =π∕2 теңдіктерінен Е жазықтығындағы(yoz жазықтығы) идеал жазық антеннаның толық өріс кернеулігін өлшеуге болатын формуланы аламыз:

Сурет 13.1 – Қоздырылған беттің сәулелену өрісін анықтау үшін

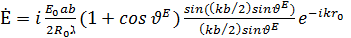(13.2)

Н жазықтығындағы (xoz жазықтығы) салдарлы өріс кернеулігін анықтайтын формуланы осыған ұқсас жолмен табамыз:

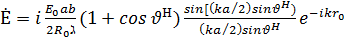(13.3)

(1+cos 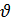) түріндегі көбейткіш –сәулеленетін бет элементінің бағыттылық сипаты (Гюйгенс элементі) – Е және Н жазықтықтарындағы бірбағыттылық қасиеттерін анықтайды.

(1+cos 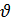) түріндегі көбейткіш 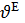және бұрыштарының өзгеруі нәтижесінде, (1+cos 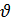) көбейткішіне қарағанда әлдеқайда тез өзгереді. Сондықтан да бір жартылай кеңістіктегі идеал жазық антеннаның бағыттылық сипаттамасы жүйе көбейткіші арқылы анықталады.

U=(ka∕2) sin 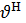және u= (ka∕2 )sin екенін белгілей отырып, жүйе көбейткішін келесі түрде жазуға болады (sinu) 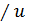және (sinυ)∕υ.

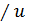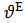(sinu) түріндегі функция u=0 болған кезде максималды және бұл максимум шамасы бірлікке тең. және υ шамалары және 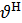бұрыштары нөлге тең болған кезде ғана нөлге тең болады.

Гюйгенс бастауы өз бетінің нормалы бағытында максималды қарқындылықпен сәулелендіретіндіктен жүйе көбейткіші максимумының бағыты және Гюйгенс бастауының бағыттылық сипаттамасы сәйкес келеді. Сондықтан идеал жазық антенна нормал бағытында максимал қарқындылықпен сәулелендіреді. (z өсінің дұрыс бағыты 13.1 суретінде келтірілген –өршітулі толқынының қозғалыс бағыты).

13.2 суретіндегі көрсетілгендей идеал сәулелендіруші беттің бағыттылық диаграммасы көп лепестокты сипаттамаға ие. Бұл антеннаның жүйе көбейткішінде осыған ұқсас синфазалық біртекті антеналық тор көбейткішінен болмашы ғана айырмашылық бар. Қорыта келгенде, бұл антеннаның бағыттылық сипаттамалары антеннаның бір элементінің бағыттылық қасиеттерін сипаттайтын көбейткіштер арқылы ерекшеленеді.

Сәулеленетін өріс нөлге айналатын бағытты келесі формула арқылы табамыз: , мұндағы N=1,2,3…., бұл жерден .

Сурет 13.2 – Сәулеленетін беттің бағытталу диаграммасы

Нөлдік сәулеленудің бірінші бағытын төмендегі формуладан табамыз:

(13.4)

(13.5)

ℷ>a және ℷ>b болған жағдайда нөлдік сәулеленудің бағыты болмайды. Нөлдік сәулелену бағыты, яғни боковой лепесток бағыты ұлғайған сайын антеннаның салыстырмалы ені де ұлғаяды (a>ℷ және b>ℷ). Егер b= және a= деп есептесек, (13.4) және (13.5) формулалары синфазалық тордың үйлесімді формулалармен сәйкес келеді.

Сәулелендіруші беттің үлкен мәндерінде [(ℷ∕) 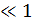және (ℷ ∕ b) 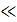1]

(13.4) және (13.5) фомулаларында синустарды аргументпен ауыстыруға болады, сонда идеал жазық антеннаның бағыттылық диаграммасының ені төмендегі формула арқылы анықталады.

Е жазықтығында:

2 =2ℷ∕b, рад; 2 = ℷ∕b, рад; (13.6)

Н жазықтығында:

2 =2ℷ∕a, рад; 2 = ℷ∕a, рад; (13.7)

Қорыта айтқанда, идеал жазық антеннаның бағыттылық диаграммасы осы жазықтыққа параллель антеннаның өлшеміне байланысты, ал перпендикуляр орналасқан антеннаның өлшеміне тәуелді болмайды.

Жартылай қуат бойынша идеал жазық антеннаның бағыттылық диаграммасының ені келесі формула арқылы анықталады.

(13.8)

(13.9)

Идеал жазық антеннаның бағыттылық диаграммасының бірінші лепесток деңгейі 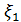=0,214.

Анализ көрсетіп тұрғандай, идеал жазық антеннаның бағыттылық диаграммасының негізгі лепестогында сәулеленуші қуаттың 82%-ы жинақталған, ал қалған 18%-ға жуығы боковой лепестокта жинақталған. Дөңгелек бетте сәулеленген өріс кернеулігінің есебі тік бұрышты антенна жағдайындағы тәсіл арқылы жасалады. Дегенмен, мұнда координатаның тікбұрышты емес, полярлы жүйесін қолданған ыңғайлы болады. Дөңгелек антенна хоу жазықтығында орналасқан р және 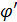– осы антеннада белгіленген элементар кеңістіктің полярлы координаттары. Бақылау нүктесінің координаталары − 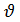( антеннаның oz өсі нормалы мен бақылау нүктесі бағыты арасындағы бұрыш) және (азимут бұрышы).

Идеал жазық дөңгелек антенна жағдайында, негізгі жазықтықтың бірін интегралдау нәтижесінде (( төмендегі формуланы аламыз:

(13.10)

мұндағы: 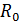−антенна радиусы, S=π ~ антенна раскрыв ауданы, 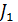− ( аргументінен Бессель нөлдік тәртібінің функциясы.

Идеал тікбұрышты антенна жағдайындағыдай, бағыттылық сипаттамасы 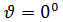болған кезде максималды.

13.2 Cәулелендіруші беттің бағыттылық диаграммасына өрістің әркелкі амплитудалық таралуының әсері

х өсін бойлай косинусты амплитудалық таралатын өрісті қарастырайық (13.3 сурет).

Сурет 13.3 – Сәулелену бетінің бағытталу диаграммасына амплитудалық таралудың әсері

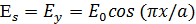(13.11)

Мұндай таралу 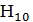толқыны арқылы өршитін тікбұрышты волноводтың ашық ұшында болады. Себебі тап осы жағдайдағы у өсін бойлай таралатын өршітуші өріс идеал антенна (бірқалыпты) жағдайындағыдай. Олай болса, қарастырылып отырған сәулелендіруші беттің бағыттылық сипаттамасы идеал жазық антенннаның бағыттылық сипаттамасынан айырмашылық болмайды. ƒ(x,y)=ƒ(x)=cos(πx∕a); υ(x,y)=0; =0, болған кезде Н векторы жазықтығындағы (xoz жазықтығы) антеннаның бағыттылық сипаттамасына арналған формуланы анықтаймыз.

(13.12)

H жазықтығында өршітуші өрісі косинусты таралатын сәулелендіруші беттің нормаланған сипаттамасы келесі формуламен анықталады:

(13.13)

Қорыта келгенде, тап осы жағдайды идеал жазық антеннамен салыстыра қарасақ, жүйе көбейткішінің түрі өзгереді.

Басты лепестоктың енін жүйе көбейткішінің алымы нөлге теңдігі шартынан табуға болады. Дегенмен косинус аргументі (ka∕2) 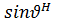π∕2 –ге тең болмау керек, өйткені бұлай болған жағдайда жүйе көбейткішінің алымы нөлге айналады да, 0/0 түріндегі белгісіздік туындайды. Сондықтан жүйе көбейткіші нөлге айналуы үшін (ka/2)sin =(3/2)π, формуласын алу қажет, бұдан sin =1,5ℷ/a. ℷ/a аз мәндерінде бұл формула 2 3ℷ/а рад. түрінде болады немесе

2 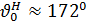ℷ/a (13.14)

Тап осы жағдайда жартылай қуат бойынша бағыттылық диаграммасының ені келесі формула арқылы анықталады:

= ℷ/a. (13.15)

Қорыта келгенде бірқалыпты амплитудалық таралдан косинус заңы арқылы түсетін сәулелендіруші беттің шекаралрындағы таралуға өту кезінде жазықтықтағы бағыттылық диаграммасының ені 1,5 есе ұлғаяды. Басты лепестоктың кеңеюімен бір уақытта боковой лепестоктың салыстырмалы деңгейі ξ=6,6% немесе -23дб−ге тең.

Бағыттылық диаграммасының кеңеюі ƒ(x)=cos(πx/a) амплитудалық таралуына сәйкес, х өсі бағытында антенна центрінен ұзақтау кезіндегі элементар кеңістіктердің жұмысының нашарлауымен түсіндіріледі. Сірә, бет шекараларына жақын орналасқан кеңістік әсерінен туындаған өрістер аз болғандықтан антеннаның салдарлы өрісінің шамасына (мөлшеріне) ықпал етпейді. Демек, антенна шектеріндегі өршітуші өріс амплитудасының кемуі осыған сәйкес өлшемдегі антеннаның біркелкі таралатын өршітуші өріс амплитудасының кемуіне эквивалентті. Алынған нәтижелерді қорытындылай отырып, келесі шешімге келеміз: өршітуші өріс амплитудасы сәулелендіруші беттің шекарасына қаншалықты тез түскен сайын бағыттылық диаграммасының басты лепестогы кеңейеді, ал боковой лепесток деңгейі төмендейді. Бұл жағдай антенналық торларда да таралған. Сәулелендіруші беттің осы қасиеті кең қолданысқа ие.

Бақылау сұраұтары:

1. Шеткі аймақтағы сәулеленетін бет өрісінің кернеулілігі?

2. Қоздырылған беттің сәулелену өрісін қалай анықтайды?

3. Сәулелену бетінің бағытталу диаграммасына амплитудалық таралудың әсері?