Лекция №9. Симметриялық вибратордың кіріс кедергісі.

9.1 Кіріс кедергінің инженерлі есептеу әдісі

Лекция жоспары:

· симметриялық вибратордың кіріс кедергісін есептеу әдістері;

· қысқа және ұзын вибратор бойынша токтың таралуы;

· сәулеленудің толық және бағытталған кедергіні есептеу.

Генератордан симметриялық вибраторға келген қуаттың бір бөлігі сәулеленеді. Ал қалған бөлігі вибратордың өзінде жоғалады, яғни оқшаулағышта (изолятор) және вибратордың айналасындағы заттарда. Сәулеленген қуат сәулеленудің активті кедергісіне сәйкес келеді. Қуат жоғалысы активті кедергі жоғалысына сәйкес келеді. Сәулеленгеннен басқа, антеннаның маңында тербелмелі, сонымен бірге реактивті қуатқа сәйкес келетін электрмагнитті өріс те бар. Бұл қуат кейде жақындағы өріске өтіп кетіп, генераторға беріледі, кейде кері өзіне қайтады. Көп жағдайда реактивті қуат антеннаның реактивті кедергісіне сәйкес келеді. Олай болса, антеннаға қосылған генератор антеннаның кіру кедергісі деп аталады. Кешенді (комплексный) кедергіге жүктелген және вибратордың қысқышындағы (зажим) кернеудің қоректендіру (питание) нүктесіндегі токқа қатынасына тең .

Кіру кедергісінің шамасы мен сипаттамасы антеннаға қосылған генератордың жұмыс режимін анықтайды. Көбінесе симметриялық вибраторда жоғалыс (потерь) аз, сондықтан 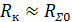деп шамалаймыз, мұндағы 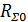- қоректену нүктеде токқа жатқызылған вибратордың сәулелену кедергісі. Кіру кедергіні дәл анықтау үшін вибратордың бойындағы токтың таралу заңын білу қажет. Инженерлік мақсатта жеткілікті жиі жағдайда кіру кедергісі вибратор бойынша токтың таралу заңына жақын есептеледі. Кіру кедергісінің есептеу әдісіне жақынын қарастырайық. Вибратордың бойындағы ток синус заңы бойынша таралған деп, симметриялық вибратордың l/λ=0,5 кіру кедергісін табамыз (сурет 9.1).

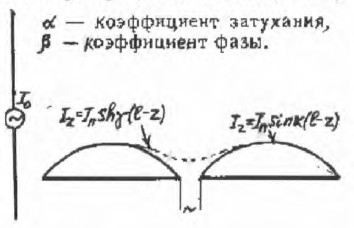
Сурет 9.1 «Қысқа» және «Ұзын» вибратор бойынша

токтың таралу

Бұл жағдайда қоректену нүктесіндегі ток нөлге тең болып шығады және 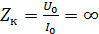екені анық. Шыныда да қоректену нүктесінде ток ешқашан нөлге тең болмайды және симметриялық вибратордың кіру нүктесі ешқашан шексіз үлкен болмайды. Бұл физикалық түрде әбден анық. Синус заңы желіде жоғалыс болмаған жағдайда ғана әділ ғой. Вибратор да сәулелену жоғалысы бар жүйе болып табылады. Кіру кедергісін есептегенде симметриялық вибратор мен ашық желінің соңындағы жоғалыс арасындағы ұқсастықты жүргізген жөн. Мұндай желідегі ток гиперболалық синус заңы бойынша таралғаны белгілі (сурет 9.1)

,

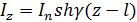мұндағы: таралу коэффициенті; α - әлсіздену коэффициенті; β - фаза коэффициенті.

9.1 суретте көрініп тұрғандай ток таралуының айналым және гиперболалық синус заңдары бойынша тек салстырмалы ток буынынан (узел) жақын арақашықтықта елеулі айырмашылық аламыз. Сондықтан «қысқа» вибратордың (l/λ)≤0,35...0,4;(0,6...0,65)≤l/λ≤(0,85...0,9) кіру нүктесін есептегенде, яғни токтың буыны вибратордың қоректену нүктесіне (0,1...0,15)λ арақашықтықтан жақын емес орналасса, токтың синусоидальді таралуына шығып кетеді. «Ұзын» вибратордың (0,35≤l/λ≤0,65) кіру кедергісін есептегенде токтың гиперболалық синус заңы бойынша таралуынан шыққан жөн. «Қысқа» вибратордың активті және реактивті құрастырылған кіру кедергісін есептейтін формула табайық. Вибратормен сәулеленген қуатты шоғырдағы токтың амплитудасы ( 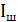) арқылы білдіреміз және қоректену нүктесінде ( 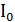) келесі формуланы аламыз:

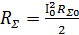және (9.1)

Формуланың сол жақ бөлігі өзара тең болғандықтан, 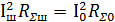болады. 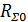қатысты теңдікті шеше оытрып, аламыз.

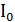орнына 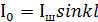мәнін қоя отырып құрастырылған кіру кедергісін есептеуге арналған формуланы аламыз (вибратордағы жоғалысты есептемегенде).

(9.2)

Вибратор үшін берілген ұзындықта 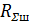шамасын кестеден немесе грфиктен табу оңай. Қысқа симметриялық вибратордың реактиті құрастырылған кіру кедергісін есептегенде жоғалыссыз екі өткізгіш желінің соңында алшақ тұрған кіру кедергісінің формуласы қолданылады және онда желінің толқындық кедергісі антеннаның толқындық кедергісімен ауыстырылады.

(9.3)

Олай болса, қысқа вибратордың толық кіру кедергісін келесі формулада анықтауға болады:

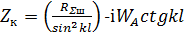(9.4)

Вибратордың көлденең қимасының өлшемі кішірейген кезде (3.20) формула бойынша есептеу дәлдігі жоғарылайды. Ұзын вибратор жағдайында кіру кедергісі жоғалысқа ие желінің соңында алшақ тұрған екі өткізгіштің кіру кедергісіне ұқсас есептелінеді.

(9.5)

мұндағы: -вибратордың толқындық кедергісі; l-вибратор иілісінің ұзындығы; α-бәсеңдеу коэффициенті; β-вибратордағы фаза коэффициенті.

Вибратор өткізгішінде жоғалысты есептемегенде, ұзын желімен ұқсастығы бойынша бәсеңдеу коэффициентін мына формула 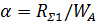бойынша есептеуге болады, мұндағы 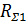- вибратор ұзындығы бірлігіне елетін сәулеленудің активті кедергісі. Вибратордың барлық ұзындығы бойынша сәулелену 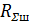біркелкі таралған деп, 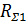есептеу үшін келесі формуланы аламыз . Бұл формула сәулелену кедергісінің ток шоғырына (пучок) қатысты екенін біле тұра, сәулеленудің таралған кедергісін анықтауға мүмкіндік берді.

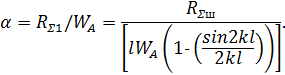
(9.5) формулада фаза коэффициенті β желідегі фазалық жылдамдық жоғалыспен және вибратордағы жарық жылдамдығынан біршама аз болғандықтан, бос кеістіктегі k фаза коэффициентімен біршама ерекшеленеді.

9.2 Сәулеленудің толық және бағытталған кедергіні есептеу

Фазасы мен амплитудасы бойынша ток тең емес 2 байланысты белсенді вибратор болсын делік. Әрбір вибратор толық сәулелену, кедергісін талап етеді. Эквивалентті схеманың вибраторларымен байланысты ауыстырамыз параметрдің жинақталған тербелмелі контуры 2 байланысынан құралады. Әрбір контур жоғары жиілікті генератордан турады, кедергі Z₁₁ немесе Z₂₂ вибраторлардың кедергісінің өзіне тең және бағытталған кедергі Z_Е12 және Z_Е21 белгісіз.

Генератордың кернеуі, контур байланысына негізделген кедергінің байланысына негізделген кедергінің байланысы және контур кедергінің жеке кернеуін түсуін толықтырып отырады. Мынаны ескереді, эквивалентті схеманың көрсеткіші үшін кирхгофа теңдеуін жахамых, кернеудің байланысы белгілі. Бұл теңдеу түрі болады.

U_П1= I_П1 Z₁₁ + I_П2 Z₁₂

U_П2= I_П2 Z_Е22 + I_П1 Z₂₁

мұндағы: U_П1 және генер U_П2 атордың бірінші және екінші кернеу, гибратордың ток нүктесі шоғыры есептелінген.

Берілген теңдеу вибратордың белгілі өзара және жеке кедергілердің тоғын сондай-ақ U_П1 және U_П2 тапсырылған кернеулерді анықтауға мүмкіндік береді. Вибратордың тоғы табылды делік, енді бағытталған кедергіні анытаймыз.

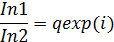
(9.6)

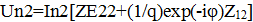(9.7)

Контурлардың (вибраторлардың) толық кедергісін білдіру үшін (9.7) теңдеуін I_n2-ге, ал (9.6) теңдеуін I_n1-ге теңдеуді бөліп аламыз.

(9.8)

(9.9)

Бағытталған және жеке сәулелену кедергінің суммасы вибратордың сәулелену кедергісі толық болса, онда вибратордың толық кедергісі мынаған тең болады:

(9.10)

(9.11)

Сондай-ақ, Ψ вибратордағы токтардың қозғалу фазасы және q токтардың амплитудасының қарым-қатынасы белгілі және вибратордың өзара кедергісі белгілі болса, онда бағытталған кедергі оңай анықталады. Толық қуаттылық, вибраторлардың 2 байланысын сәулелендіреді, мына теңдеуге тең: P_Σ=P_Σ1+P_Σ2= I_n1² _RΣ11/2+ I_n2² R_Σ21/2

Вибратордың байланысты кіріс кедергісі формула бойынша есептелінуі мүмкін, сондай-ақ кіріс кедергісі инденерлік есептеулерде қолданылады. Қысқа вибраторлардың жағдайында вибратордың байланысты кіріс кедергісі мына формула бойынша анықталады.

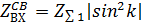немесе 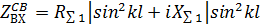(9.12)

Z_Σ1- вибратор байланысының толық сәулелену кедергісі. Ұзын вибратордың жағдайында байланыс вибратордың кіріс кедергісі 9.8 формуласы бойынша есептелінеді.

Бір вибратордың толқындық кедергісі басқа вибраторға әсер етуімен және оның коэффицентінің өшуі. (9.13) осы формулада берілген:

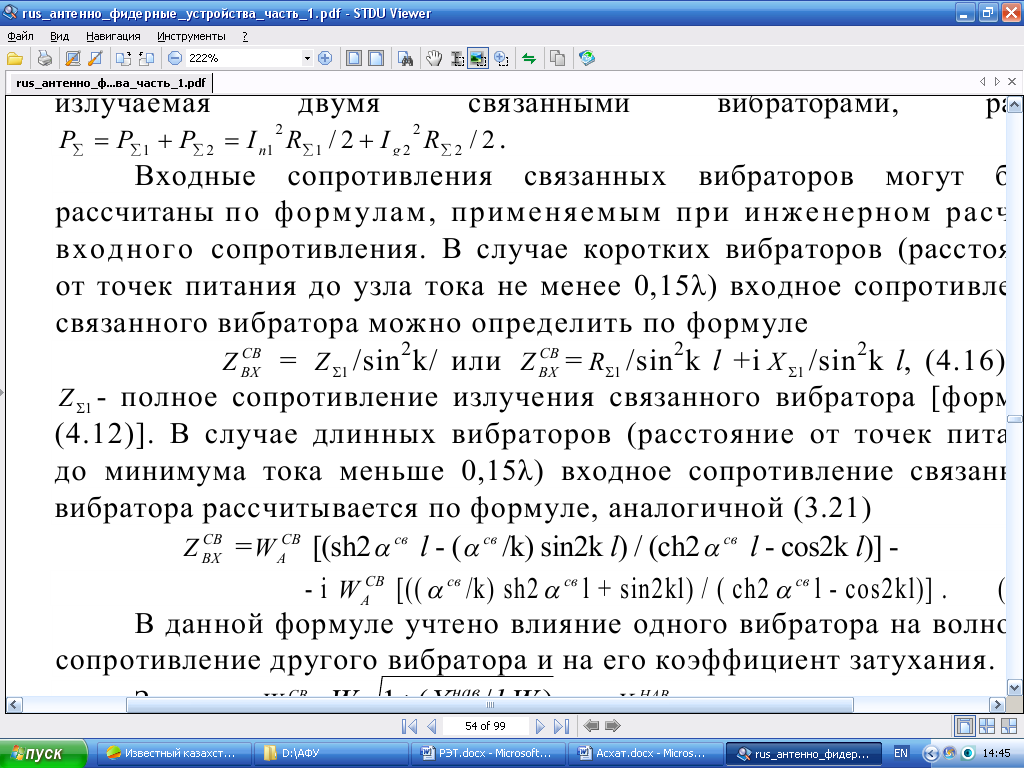
(9.13)

мұндағы: 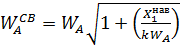, 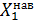реактивті бағытталған кедергі мен вибратордың ұзындығы мына формула бойынша анықталады:

(9.14)

Бақылау сұрақтары:

1. Симметриялық вибратордың кіріс кедергісін есептеу әдістерін айтып беріңіз?

2. Антеннаның кіру кедергісі дегеніміз не?

3. Сәулеленудің толық және бағытталған кедергілерінің айырмашылығын түсіндіріп беріңіз?