Помехостойкость шифров.

Помимо целенаправленных искажений передаваемой шифрованной информации возможны также искажения, происходящие за счет наличия помех в канале связи. Такие помехи могут привести к искажениям и даже потере некоторых знаков используемого алфавита. Если искаженный знак не является знаком используемого алфавита, то на приеме факт искажения легко установить. В противном случае факт искажения может быть установлен лишь при расшифровании, когда искажение в шифртексте ведет к потере части или даже всего открытого текста. Так же проявляется и потеря знаков шифртекста.

Прежде всего интересен вопрос о свойствах самого шифра, позволяющих не распространять искажений при расшифровании. Ограничимся только рассмотрением эндоморфных (X=Y) шифров и искажений двух типов:

1. Замена знаков знаками того же алфавита.

2. Потеря знаков или появление дополнительных знаков того же алфавита.

Шифры, не распространяющие искажений типа "замена знаков".

Будем рассматривать шифры, описываемые алгебраической моделью

S_A = (X, K, Y, E, D),

в которой 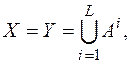причем для любых x Î X и k Î K длина y = E_k(x) совпадает с длиной x.

Мерой значительности последствий искажений типа "замена знаков" является метрика на множестве сообщений X = Y. Простейшей является метрика Хэмминга m,определяемая формулой

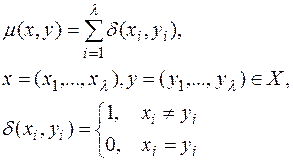
Так как для эндоморфного шифра каждое правило зашифрования E_k представляет собой биекцию E_k : X ® X, то будем пользоваться подстановочной моделью шифра - S_П = (X, E),в которой множество E ={e_k : k Î K} рассматривается как множество подстановок e : X ® X, e Î E.

Шифр S_П = (X, E)не распространяет искажений типа замены знаков и являются помехостойкими если для любых x, y Î A^l и любого e Î E выполняется неравенство

m(e^-1x, e^-1y) £ m(x, y).

Подстановки e Î E, удовлетворяющие предыдущему равенству, называются изометриями на X.

Теорема А. А. Маркова. Биекция eÎE является изометрией на X тогда и только тогда, когда 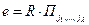для подходящих преобразований множества X:

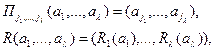
где (j₁,…,j_l) – перестановка чисел 1, 2, …, l; R_i Î S(A) – некоторые фиксированные подстановки множества A, a_i Î A,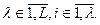

Согласно теореме Маркова, в классе эндоморфных шифров, не изменяющих длины сообщений, не распространяют искажения типа замены знаков, например шифры перестановки, поточные шифры однозначной замены, а также их композиции типа шифр замены – шифр перестановки.

Шифры, не распространяющие искажений типа "пропуск-вставка знаков".

Приведем теорему, рассматривающую подстановочную модель шифра.

Теорема. Если S_П = (X, E)– шифр не распространяющий искажений типа пропуск-вставка, то для любого e Î E, либо e = p_L, либо у = p_L · f (при подходящем p Î S(A)), где p_L отображение множества X в себя, определенное для любого a = (a₁,…,a_l) Î X формулой

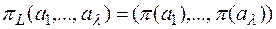
(p - некоторая подстановка множества A), а f – отображение множества X в себя, меняющее порядок следования букв любого слова на противоположный:

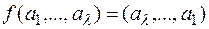
Всякий шифр, не распространяющий искажений типа "пропуск-вставка знака" есть либо шифр простой замены либо произведение шифра простой замены и частного вида шифра перестановки, заключающейся в инверсной записи текста (справа налево).

Следовательно, все сложные шифры распространяют искажения типа "пропуск-вставка" и в данном случае борьба с такими искажениями криптографическими методами невозможна и, следовательно, необходимо применять иные способы повышения помехоустойчивости (например, введением избыточности – контрольные суммы и пр.).

Практические вопросы повышения надежности.

Совместно с алгоритмом шифрования данных целесообразно использовать алгоритм сжатия по следующим причинам:

· Криптоанализ опирается на избыточность шифртекста, а сжатие файла перед шифрованием эту избыточность снижает;

· Шифрование занимает много времени, а потому сжатие файла до шифрования ускоряет весь процесс.

Важно запомнить, что сжатие должно выполняться именно до шифрования. (Сжимаемость шифртекста можно использовать как неплохой тест алгоритма шифрования. Если шифртекст можно сжать, значит алгоритм не сишком надежен.)

Вырабатывать имитовставку можно до сжатия файла и сжимать вместе с ним с целью повышения стойкости шифра. (Имитовставка повышает избыточность текста.) Или же выполнять после шифрования, с целью ускорения процесса аутентификации сообщения.

Помехоустойчивое кодирование, повышающее избыточность текста, наоборот целесообразно применять после шифрования данных.

Последовательность применения имитовставки и кодирования приведена на рис.12.

Рис. 12. Практическое применение имитовставки в сочетании со сжимающим и помехоустойчивым кодированием.

Контрольные вопросы

1. Назовите основные составляющие алгебраической модели шифра.

2. Для чего применяются вероятностные модели шифров?

3. Для чего применяются модели открытых текстов?

4. Назовите критерии на открытый текст.

5. В чем различие между теоретической и практической криптостойкостью шифров?

6. В чем различие между имитацией и подменой сообщения?

7. Назовите основные способы обеспечения имитостойкости.

8. Какие бывают виды искажений при передаче сообщения?