Статистическое определение вероятности

Классическое определение вероятности при переходе от простейших примеров к рассмотрению сложных задач, в особенности же задач естественнонаучного или технического характера, становится не применимым. Прежде всего здесь возникает вопрос о возможности нахождения разумного способа выделения "равновоз­можных" событий. Как, например, из соображений симметрии, на которых основаны наши суждения о равновероятности событий, вывести вероятность распада радиоактивного вещества за определенный промежуток времени; или как определить вероятность того, что родившийся ребенок окажется мальчиком. В этих случаях, еще на заре возникновения теории вероятностей, был найден иной способ приближенной оценки неизвестной вероятности случайного события.

Относительной частотой появления события А называется отношение

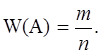(1.8)

где n – число опытов, m – число появлений события А.

Длительные наблюдения над появлением и непоявлением события А при большом числе независимых испытаний, производимых при одном и том же комплексе условий, в ряде случаев показывают, что число появлений события А подчиняется устойчивым закономерностям. Еще в XVII в. Я. Бернулли доказал (см. закон больших чисел Бернулли), что при неограниченном увеличении числа опытов относительная частота будет практически сколь угодно мало отличаться от некоторого постоянного числа, которое и принимается за вероятность события в отдельном опыте.

Статистической вероятностью называется относительная частота появления события при неограниченном увеличении числа испытаний:

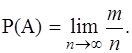(1.9)

Примером статистической вероятности может являться число 0,514 – средне статистическая вероятность рождения мальчиков. Статистическое определение вероятности широко используется на практике, особенно в естествознании. Здесь для определения вероятности используются различные методы математической статистики. Более того, статистическое определение вероятности немецкий математик Р. Мизес положил в основу частотной теории вероятностей. Однако при таком подходе теория вероятностей будет всего лишь прикладной наукой, в которой широко используются математические методы. Отметим, что статистический подход к определению вероятности обладает рядом недостатков. Во-первых, объективно невозможно осуществить произвольное число испытаний; во-вторых, статистическую вероятность можно определить только после опыта, по его результатам, т.е. статистический подход не обладает предсказательной силой.

В заключение отметим, что между всеми рассматриваемыми определениями вероятности (классическим, геометрическим, статистическим) нет принципиального различия. Все они являются всего лишь различными походами к определению одной и той же объективной реальности, которая называется вероятностью.