Размещения и перестановки

Пусть имеется некоторое множество, содержащее n элементов. Выберем из этого множества k элементов без возвращения, но упорядочивая их по мере их выбора в последовательную цепочку. Такие цепочки называются размещениями.

Размещением из n элементов по k элементов называется любое упорядоченное подмножество из k элементов исходного множества, содержащего n различных элементов.

Число размещений 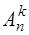можно найти из принципа умножения. Первый элемент размещения можно выбрать n способами. Как только такой выбор будет сделан, останется (n–1) возможностей, чтобы выбрать второй элемент; после этого останется (n–2) возможностей для выбора третьего элемента и т.д.; для выбора k-го элемента будет (n–k+1) возможностей. По принципу умножения находим

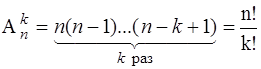. (1.1)

Легко понять, что .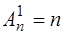

Пример 1.7. В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить 4 фотографии. Сколькими способами это можно сделать, если ни одна страница газеты не должна содержать более одной фотографии?

Решение. Для размещения фотографий следует отобрать 4 различных страницы из 12 имеющихся. Затем нужно отобранные страницы упорядочить, т.е. определить, на какую страницу поместить первую фотографию, на какую – вторую и т.д. Полученная упорядоченная совокупность страниц является, согласно определению, размещением из 12 элементов по 4, а число таких размещений является искомым результатом:

.

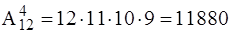Рассмотрим частный случай, когда k=n. Соответствующее этому случаю размещение называется перестановкой.

Перестановкой из n элементов называется любой упорядоченное множество, в которое входят по одному разу все n различных элементов данного множества.

Отметим, что перестановки состоят из одних и тех же элементов, но отличаются между собой порядком. Число перестановок n различных элементов обозначают символом P_n и равно

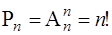(1.2)

Пример 1.8. Сколькими способами можно расставить девять различных книг на полке, чтобы определенные четыре книги стояли рядом?

Решение. Будем считать выделенные книги за одну книгу. Тогда уже для шести книг существует P₆=6!=720 перестановок. Однако четыре определенные книги можно переставить между собой P₄=4!=24 способами. По принципу умножения имеем

P₆P₄ = 720×24 = 17280.

Сочетания

Пусть опыт состоит в выборе k элементов без возвращения и без упорядочения из некоторого множества, содержащего n элементов. Исходами такого опыта будут подмножества, содержащие k элементов и отличающиеся друг от друга только составом. Получаемые при этом комбинации элементов называются сочетаниями.

Сочетаниями из n элементов по k называется любое подмножество из k элементов, которые принадлежат множеству, состоящему из n различных элементов.

Например, при выборе делегации в составе 3 человек из 30 студентов, очевидно, не надо учитывать порядок выбранных делегатов, т.к. все члены делегации равноправны. Поэтому каждый такой выбор будет сочетанием из 30 по 3. Однако, выбирая старосту, профорга и физорга из тех же студентов, порядок уже приходится учитывать. В этом случае каждый конкретный результат будет уже размещением из 30 по 3.

Найдем число возможных сочетаний С_n^k. Чтобы получить размещение из n элементов по k, а их число равно A_n^k, надо выбрать k элементов из множества, содержащего n элементов, что можно сделать C_n^k способами, и организовать из них упорядоченное подмножество. Последнюю операцию можно выполнить P_n способами. Таким образом, чтобы получить A_n^k размещений, надо выполнить две операции, которые можно осуществить С_n^k и Р_n способами, соответственно. Поэтому, согласно принципу умножения, можно записать

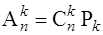. (1.3)

Отсюда получаем

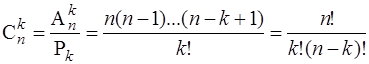. (1.4)

Заметим, что С_n⁰=C_nⁿ=1, C_n¹=n.

Пример 1.9. Сколькими способами можно составить комиссию в составе из трех человек из имеющихся 9 человек, 4 женщин и 5 мужчин, если: а) не важен пол членов комиссии; б) комиссия должна состоять из двух женщин и одного мужчины.

Решение. а) Из смысла задачи следует, что порядок выбора членов комиссии не играет роли. Здесь важен только состав. Тогда выбрать комиссию из трех человек из 9 имеющихся можно

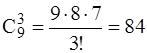
способами.

б) Двух женщин из 4 имеющихся можно выбрать С₄² способами, а одного мужчину из 5 можно С₅¹ способами. тогда общее количество способов выбора комиссии, в соответствии с принципом умножения, можно

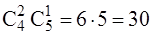
способами.

Отметим, что при использовании сочетаний могут быть полезны следующие свойства:

1⁰. 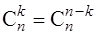(свойство симметрии),

2⁰. ,

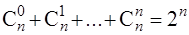3⁰. 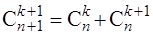(свойство Паскаля).