Геометрическое определение вероятности

Классическая формула вероятности предполагает конечное число всех исходов испытания. Но часто встречаются такие испытания, для которых число возможных исходов бесконечно. В подобных случаях классическая формула вероятности не применима и в этом заключается один из недостатков классического определения вероятности. Например, в теории стрельбы точность попадания равна расстоянию от центра мишени до точки попадания и может принимать любое значение. Если под опытом понимать один выстрел, то в результате такого опыта возможно бесконечное множество исходов.

Геометрической вероятностью события А называется отношение меры области g, благоприятствующей появлению события А, к мере всей области G, в каждой точке которой с равной вероятностью могут осуществляться исходы рассматриваемого опыта:

(1.7)

Мера – это сложное математическое понятие. В простейшем случае это может быть длина (для одномерных областей, например, длина какой-нибудь кривой), площадь (для двухмерных областей, например, площадь какой-нибудь поверхности), объем (для трехмерных областей, например, объем некоторого тела в пространстве).

Пример 1.15. На плоскость нанесена сетка квадратов со стороной 8 см. Найти вероятность того, что брошенный на плоскость круг радиуса 1 см не пересечет ни одной стороны квадрата (событие А).

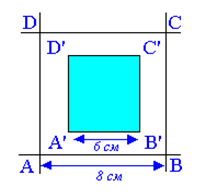Решение. При бросании круга его центр может попасть с равной вероятностью в любой из квадратов, начерченных на плоскости. Поскольку все квадраты одина­ковы, то, не уменьшая общности, можно рассмотреть только один квадрат. Сделаем внутри квадрата "рамку" шириной 1 см. Если центр круга попадет в "рамку", то круг обязательно пересечет сторону квадрата. Если же центр круга попадет в заштрихованную область, то он не пересечет ни одной стороны квадрата. Таким образом, заштрихованный квадрат является благоприятствующей областью наступления события А, вероятность которого нужно найти. В результате получаем:

Геометрический поход к вычислению вероятностей можно использовать в некоторых случаях и для негеометрических задач:

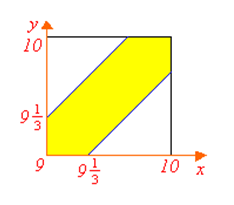Пример 1.16. Два человека А и В решили встретиться между 9 и 10 часами. Причем каждый ждет друг друга в течение 20 мин. Чему равна вероятность того, что они встретятся, если моменты прихода каждого из них в течение указанного времени равновероятны.

Решение. Обозначим моменты прихода лица А через x, а лица В через y. Для того чтобы встреча состоялась, необходимо и достаточно, чтобы

Примем x и y в качестве декартовых координат на плоскости xOy. Тогда всевозможные исходы будут изображаться точками квадрата; благоприятствующие встрече – располагаться в заштрихованной области (см. рис.). Искомая вероятность равна отношению площади заштрихованной фигуры к площади всего квадрата: