Лекция 6 Тепловые двигатели. Реальные газы. Явления переноса
План
1. Круговой процесс (цикл). Цикл Карно и его КПД для идеального теплового двигателя. Второе начало термодинамики. Независимость КПД цикла Карно от природы рабочего тела.
2. Реальные газы. Уравнение Ван-дер-Ваальса. Сравнение изотерм Ван-дер-Ваальса с экспериментальными. Явления переноса.
Тезисы:
1. Термический коэффициент полезного действия для кругового процесса 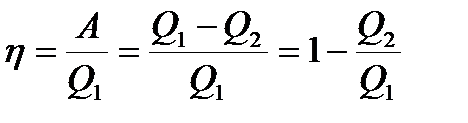 , где Q1— количество теплоты, полученное системой, q2— количество теплоты, отданное системой. Приведенное количество теплоты - отношение теплоты Q, полученной телом в изотермическом процессе, к температуре Т теплоотдающего тела, dQ / T. Приведенное количество теплоты, сообщаемое телу в любом обратимом круговом процессе, равно нулю:
, где Q1— количество теплоты, полученное системой, q2— количество теплоты, отданное системой. Приведенное количество теплоты - отношение теплоты Q, полученной телом в изотермическом процессе, к температуре Т теплоотдающего тела, dQ / T. Приведенное количество теплоты, сообщаемое телу в любом обратимом круговом процессе, равно нулю: 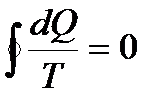 или
или 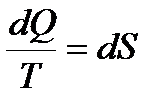 Функция состояния, дифференциалом которой является dQ/T, называется энтропией и обозначается S. Неравенство Клаузиуса
Функция состояния, дифференциалом которой является dQ/T, называется энтропией и обозначается S. Неравенство Клаузиуса 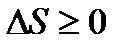 Энтропия замкнутой системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов).
Энтропия замкнутой системы может либо возрастать (в случае необратимых процессов), либо оставаться постоянной (в случае обратимых процессов).
Изменение энтропии DS1®2 идеального газа при переходе его из состояния 1 в состояние 2 не зависит от вида процесса перехода: 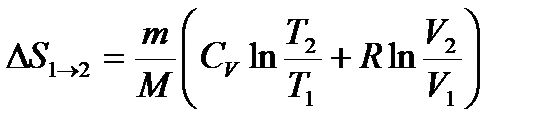
Адиабатический обратимый процесс протекает при постоянной энтропии.
При изотермическом процессе 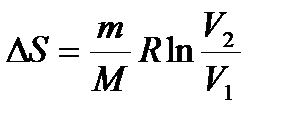 , при изохорном
, при изохорном 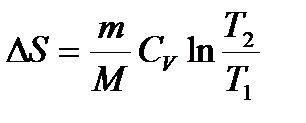
Термодинамическая вероятность W состояния системы — это число способов, которыми может быть реализовано данное состояние макроскопической системы.
Формула Больцмана 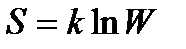 (энтропия определяется логарифмом числа микросостояний, с помощью которых может быть реализовано данное макросостояние).
(энтропия определяется логарифмом числа микросостояний, с помощью которых может быть реализовано данное макросостояние).
Статистическое толкование энтропии Энтропия является мерой неупорядоченности системы. Процессы в замкнутой системе идут в направлении от менее вероятных состояний к более вероятным, до тех пор, пока вероятность состояния не станет максимальной. Энтропия и термодинамическая вероятность состояний замкнутой системы могут либо возрастать (в случае необратимых процессов), либо оставаться постоянными (в случае обратимых процессов). Эти утверждения выполняются в системах, состоящих из очень большого числа частиц.Энтропия пропорциональна вероятности пребывания системы в определенном состоянии. Наиболее вероятным состоянием системы, состоящей из большого числа частиц, будет состояние, когда все частицы равномерно распределены по всему объему системы, т.е. они распределены хаотически. Поэтому возрастание энтропии означает, что любая система стремится в состояние с наибольшей вероятностью. Другими словами, наиболее вероятным состоянием системы является состояние полного хаоса.
Формулировки второго начала термодинамики
1. любой необратимый процесс в замкнутой системе происходит так, что энтропия системы при этом возрастает;
2. невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу;
3. невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому.
Третье начало термодинамики (теорема Нернста — Планка): энтропия всех тел в состоянии равновесия стремится к нулю по мере приближения температуры к абсолютному нулю: 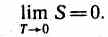
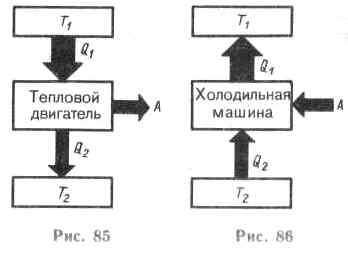
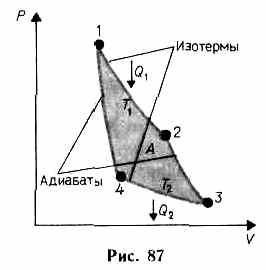
Теорема Карно: из всех периодически действующих тепловых машин, имеющих одинаковые температуры нагревателей (T1) и холодильников (Т2), наибольшим к. п. д. обладают обратимые машины; при этом КПД обратимых машин, работающих при одинаковых температурах нагревателей (T1) и холодильников (T2), равны друг другу и не зависят от природы рабочего тела (тела, совершающего круговой процесс и обменивающегося энергией с другими телами). Цикл Карно – обратимый, наиболее экономичный цикл, состоящий из двух изотерм и двух адиабат
КПД цикла Карно 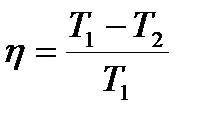
2. Ван-дер-Ваальс первый сумел создать новую модель реального газа:
1) между молекулами действуют силы притяжения, которые по своей природе являются электрическими. Каждая молекула - шар диаметра d. Поэтому величину объема, входящего в уравнение Менделеева - Клапейрона, надо заменить на новую величину (V-b), где b рассматривается как некоторая поправка на истинный объем, доступный молекулам газа; 2) молекулы взаимодействуют не только друг с другом, но и с окружающими их стенками сосуда. Если силы взаимодействия между молекулами вдали от стенки в среднем компенсируют друг друга, то вблизи стенки на молекулу действует некоторая равнодействующая сила, направленная от стенки и стремящаяся уменьшить кинетическую энергию молекулы при ее ударе об стенку.
Уравнение Ван-дер-Ваальса (для 1 моль реального газа) 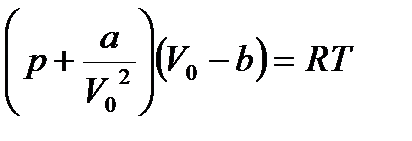 , где а и в – постоянные для каждого газа величины, определяемые опытным путем. Для произвольного количества вещества)
, где а и в – постоянные для каждого газа величины, определяемые опытным путем. Для произвольного количества вещества) 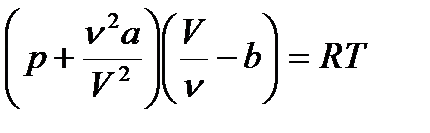
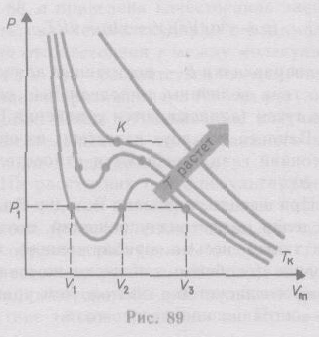
Для исследования поведения реального газа рассмотрим изотермы Ван-дер-Ваальса - кривые зависимости р от Vm при заданных Т, определяемые уравнением Ван-дер-Ваальса для моля газа. Эти кривые (рассматриваются для четырех различных температур) имеют довольно своеобразный характер. При высоких температурах (T>Tк) изотерма реального газа отличается от изотермы идеального газа только некоторым искажением ее формы, оставаясь монотонно спадающей кривой. При некоторой температуре Тк на изотерме имеется лишь одна точка перегиба К. Эта изотерма называется критической, соответствующая ей температура Tк — критической температурой. Критическая изотерма имеет лишь одну точку перегиба К, называемую критической точкой; в этой точке касательная к ней параллельна оси абсцисс. Соответствующие этой точке объем Vк и давление рк называются также критическими. Состояние с критическими параметрами (рк, Vк, Тк) называется критическим состоянием. При низких температурах (Т<Тк) изотермы имеют волнообразный участок, сначала монотонно опускаясь вниз, затем монотонно поднимаясь вверх и снова монотонно опускаясь.
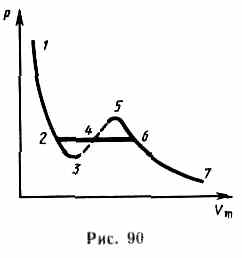
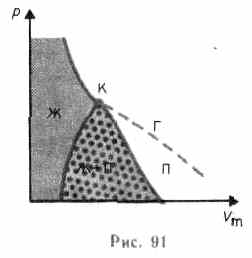
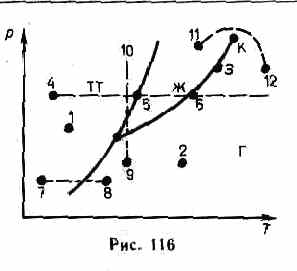
Кривая, соответствующая уравнению Ван-Дер-Ваальса, пересекает горизонтальную прямую - изобару - в трех точках. Однако сразу становится ясным, что не все участки теоретической кривой могут быть реализованы. В частности, на участке 3-5 увеличение объема сопровождается увеличением давления, что противоречит здравому смыслу. Газ же при температуре выше критической не может быть превращен в жидкость ни при каком давлении.
Участок 2—6 соответствующий двухфазным состояниям вещества. Правда, при некоторых условиях могут быть реализованы состояния, изображаемые участками ван-дер-ваальсовой изотермы 5—6 и 2—3. Эти неустойчивые состояния называются метастабильными. Участок 2—3 изображает перегретую жидкость, 5—6 — пересыщенный пар. Обе фазы ограниченно устойчивы. При достаточно низких температурах изотерма пересекает ось Vm, переходя в область отрицательных давлений. Вещество под отрицательным давлением находится в состоянии растяжения. При некоторых условиях такие состояния также реализуются.
Уравнение Клайперона – Клаузиуса: производная от равновесного давления по температуре 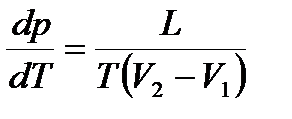 , где L – теплота фазового перехода, T - температура перехода (процесс изотермический). Уравнение позволяет определить наклоны кривых равновесия.
, где L – теплота фазового перехода, T - температура перехода (процесс изотермический). Уравнение позволяет определить наклоны кривых равновесия.
Явления переноса возникают в газах в результате нарушения полной хаотичности движения молекул. Эти нарушения вызваны направленным воздействием на газ, приводящим в случае диффузии к неоднородной плотности, в случае теплопроводности – к разной температуре в различных слоях объема газа. Внутреннее трение связано с тем, что создается упорядоченное движение различных слоев газа с различными скоростями. Нарушение полной хаотичности движения молекул в явлениях переноса сопровождается отклонением от максвелловского закона распределения молекул по скоростям. Именно отклонениями от этого закона объясняется направленный перенос массы, импульса и внутренней энергии в газах.
Теплопроводность Для простоты ограничимся одномерными явлениями переноса. Систему отсчета выберем так, чтобы ось Х была ориентирована в направлении переноса. Если в одной области газа средняя кинетическая энергия молекул больше, чем в другой, то с течением времени вследствие постоянных столкновений молекул происходит выравнивание средних кинетических энергий молекул, т.е. выравнивание температур. Закон Фурье 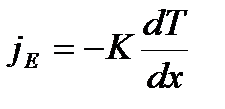 Коэффициент теплопроводности
Коэффициент теплопроводности 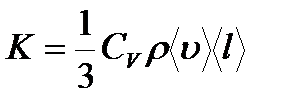 , где jE - плотность теплового потока – величина, определяемая энергией, переносимой в форме теплоты в единицу времени через единичную площадку, перпендикулярную оси Х, К – теплопроводность (коэффициент теплопроводности), dT/dx - градиент температуры, равный скорости изменения температура на единицу длины Х в направлении нормали к этой площадке. Знак «минус» в формуле показывает, что при теплопроводности энергия переносится в направлении убывания температуры. Теплопроводность К численно равна плотности теплового потока при градиенте температуры, равном единице.
, где jE - плотность теплового потока – величина, определяемая энергией, переносимой в форме теплоты в единицу времени через единичную площадку, перпендикулярную оси Х, К – теплопроводность (коэффициент теплопроводности), dT/dx - градиент температуры, равный скорости изменения температура на единицу длины Х в направлении нормали к этой площадке. Знак «минус» в формуле показывает, что при теплопроводности энергия переносится в направлении убывания температуры. Теплопроводность К численно равна плотности теплового потока при градиенте температуры, равном единице.
Явление диффузии заключается в том, что происходит самопроизвольное проникновение и перемешивание частиц двух соприкасающихся тел; диффузия сводится к обмену масс этих частиц, возникает и продолжается, пока существует градиент плотности. Во время становления МКТ по вопросу диффузии возникали противоречия. Так как молекулы движутся с огромными скоростями, диффузия должна происходить очень быстро. Если же открыть в комнате сосуд с пахучим веществом, то запах распространится очень медленно. Однако противоречия здесь нет. Молекулы при атмосферном давлении обладают малой длиной свободного пробега и, сталкиваясь с другими молекулами, в основном «стоят» на месте.
Закон Фика 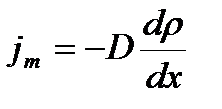 Коэффициент диффузии
Коэффициент диффузии 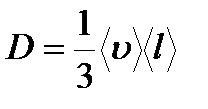 , где jm – плотность потока массы – величина, определяемая массой вещества, диффундирующего в единицу времени через единичную площадку, перпендикулярную оси Х, D - диффузия (коэффициент диффузии), dρ / dx - градиент плотности, равный скорости изменения плотности на единицу длины Х в направлении нормали к этой площадке. Знак минус показывает, что перенос массы происходит в направлении убывания плотности. Диффузия D численно равна плотности потока массы при градиенте плотности, равном единице.
, где jm – плотность потока массы – величина, определяемая массой вещества, диффундирующего в единицу времени через единичную площадку, перпендикулярную оси Х, D - диффузия (коэффициент диффузии), dρ / dx - градиент плотности, равный скорости изменения плотности на единицу длины Х в направлении нормали к этой площадке. Знак минус показывает, что перенос массы происходит в направлении убывания плотности. Диффузия D численно равна плотности потока массы при градиенте плотности, равном единице.
Механизм возникновения внутреннего трения между параллельными слоями газа (жидкости), движущимися с различными скоростями, заключается в том, что из-за хаотического теплового движения происходит обмен молекулами между слоями, в результате чего импульс слоя, движущегося быстрее, уменьшается, движущегося медленнее – увеличивается, что приводит к торможению слоя, движущегося быстрее, и ускорение слоя, движущегося медленнее.
Сила внутреннего трения между двумя слоями газа (жидкости) подчиняется закону Ньютона: 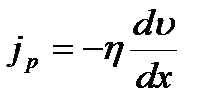 Динамическая вязкость
Динамическая вязкость 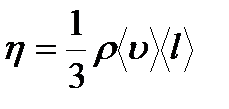 , где jp – плотность потока импульса – величина, определяемая полным импульсом, переносимым в единицу времени в положительном направлении оси Х через единичную площадку, перпендикулярную оси Х, dv / dx - градиент скорости. Знак минус показывает, что импульс переносится в направлении убывания скорости. Динамическая вязкость численно равна плотности потока импульса при градиенте скорости, равном единице. Между коэффициентами переноса зависимости:
, где jp – плотность потока импульса – величина, определяемая полным импульсом, переносимым в единицу времени в положительном направлении оси Х через единичную площадку, перпендикулярную оси Х, dv / dx - градиент скорости. Знак минус показывает, что импульс переносится в направлении убывания скорости. Динамическая вязкость численно равна плотности потока импульса при градиенте скорости, равном единице. Между коэффициентами переноса зависимости: 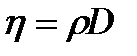 и
и 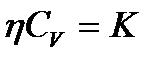
Дата добавления: 2016-03-10; просмотров: 1445;
