ПОНЯТИЕ О КОНЦЕНТРАЦИИ НАПРЯЖЕНИЙ, ПРИНЦИП СЕН-ВЕНАНА
Даже для призматического стержня равномерное распределение напряжений по поперечному сечению не всегда имеет место. Так, отклонения от равномерного распределения напряжений наблюдаются в окрестности сечений, содержащих вырезы, выточки, отверстия, трещины, в местах резкого изменения поперечного сечения, а также в местах приложения сосредоточенных сил и т. п. Неравномерное распределение напряжений в указанных местах является следствием искажения плоскостей поперечных сечений или их депланации.
Поясним это явление на примере подверженной растяжению полосы из податливого материала с круговым отверстием, на поверхности которой нанесены продольные и поперечные риски (рис. 5, а). В зоне отверстия имеет место депланация поперечных сечений, вызванная неравномерным растяжением продольных волокон (рис.5, б). При этом наибольшие удлинения и соответственно напряжения max 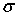 получают волокна возле отверстия. Такое местное увеличение напряжений возле вырезов, выточек, отверстий и т. п., а также в местах приложения сосредоточенных сил, называется у концентрацией напряжений, а источники концентрации напряжений (вырезы, выточки, отверстия и т. п.) получили название концентраторов напряжений.
получают волокна возле отверстия. Такое местное увеличение напряжений возле вырезов, выточек, отверстий и т. п., а также в местах приложения сосредоточенных сил, называется у концентрацией напряжений, а источники концентрации напряжений (вырезы, выточки, отверстия и т. п.) получили название концентраторов напряжений.

Рис.5. Концентрация напряжений: а) исходное состояние, б) деформированное состояние, в) распространение напряжений
Рассмотренными методами механики деформированного тела, опирающимися на гипотезу плоских сечений, задачи о распределении напряжений в зонах концентрации напряжений не решаются. Такие задачи решаются методами теории упругости или исследуются экспериментально. При этом для практических расчетов вводится так называемый теоретический коэффициент концентрации напряжений 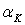 , представляющий собой отношение максимальных max
, представляющий собой отношение максимальных max 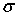 и номинальных
и номинальных 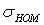 напряжений:
напряжений: 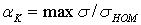 , где номинальные напряжения определяются без учета концентрации напряжений. В приведенном примере растяжения полосы с отверстием
, где номинальные напряжения определяются без учета концентрации напряжений. В приведенном примере растяжения полосы с отверстием 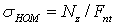 , a Fnt — площадь поперечного сечения полосы, уменьшенная за счет отверстия («нетто»). Таким образом,
, a Fnt — площадь поперечного сечения полосы, уменьшенная за счет отверстия («нетто»). Таким образом, 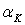 играют роль поправочных коэффициентов.
играют роль поправочных коэффициентов.
Однако, как показали эксперименты и точные решения задач теории упругости, местные отклонения от равномерного распределения напряжений, вызванные концентрацией напряжений, быстро затухают по мере удаления от сечения с концентратором, и на расстояниях порядка ширины сечения распределение напряжений можно считать практически равномерным (рис. 5, в). Отмеченное свойство является частным случаем широко используемого практически во всех разделах механики деформируемого твердого тела (в том числе и теории упругости) принципа Сен-Венана
Дата добавления: 2016-03-05; просмотров: 1101;
