Основы технической термодинамики, теплопередачи и гидродинамики
Технической термодинамикой называется наука, изучающая свойства тепловой энергии и законы взаимного превращения тепловой и механической энергии. Техническая термоди-намика является основой теории двигателей внутреннего сгорания. Всякая тепловая маши-на приводится в действие вследствие происходящего в ней изменения состояния вещества, называемого рабочим телом или рабочим агентом.
Совокупность тел, находящихся в тепловом и механическом взаимодействии друг с другом и окружающей средой, называется термодинамической системой.
Рабочее тело определяет тип и назначение тепловой машины. Наиболее эффективными рабочими телами для тепловых машин являются пар и газы, обладающие наибольшим коэффициентом объемного расширения. Для термодинамического анализа работы тепловой машины необходимо знать термодинамические свойства рабочего тела.
В качестве основных термодинамических параметров состояния газообразного вещества выступают абсолютная температура, абсолютное давление, удельный объем и др.
Температура газа служит мерой кинетической энергии поступательного движения молекул газа и характеризует степень его нагрева. В настоящее время в термодинамике в качестве основной принята термодинамическая температурная шкала, где нижней границей шкалы является температура абсолютного нуля (практически недостижимая), когда прекращается тепловое движение молекул. Единица температуры по термодинамической температурной шкале получила название Кельвин. Соотношение между шкалой Цельсия и шкалой Кельвина
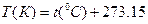
где 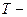 температура термодинамической шкале;
температура термодинамической шкале; 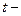 температура по шкале Цельсия.
температура по шкале Цельсия.
Абсолютная температура, измеряемая в кельвинах, является параметром состояния.
Давление— физическая величина, характеризующая интенсивность сил, действующих по нормали к поверхности тела и отнесенных к единице площади этой поверхности, т.е.
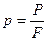 где
где 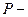 сила в ньютонах;
сила в ньютонах; 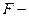 площадь в
площадь в 
Для измерения давления применяются различные единицы: Паскаль (Па), бар, техническая атмосфера или просто атмосфера, миллиметр ртутного или водяного столба, которые находятся в следующих соотношениях: 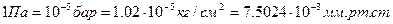
Различают абсолютное, избыточное и вакуумметрическое давление. На практике за начало отсчета обычно принимают атмосферное (барометрическое) давление, которое зависит от массы слоя воздуха. Нормальное давление - это барометрическое давление, равное одной физической атмосфере и составляет примерно 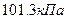 или
или 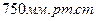 Абсолютным давлением называется давление газов и жидкостей в закрытых объемах и, которое не зависит от состояния окружающей среды. Если абсолютное давление больше атмосферного, то разность между ними характеризует избыточное (манометрическое) давление:
Абсолютным давлением называется давление газов и жидкостей в закрытых объемах и, которое не зависит от состояния окружающей среды. Если абсолютное давление больше атмосферного, то разность между ними характеризует избыточное (манометрическое) давление: 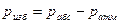 . Если абсолютное давление меньше атмосферного, то разность между ними называется разрежением, или вакуумом:
. Если абсолютное давление меньше атмосферного, то разность между ними называется разрежением, или вакуумом: 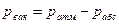 . Вышеприведенные формулы показывают, что при неизменном состоянии газа в сосуде постоянным остается лишь значение абсолютного давления
. Вышеприведенные формулы показывают, что при неизменном состоянии газа в сосуде постоянным остается лишь значение абсолютного давления 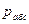 а
а 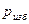 и
и 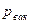 изменяются при изменении
изменяются при изменении 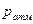 . Поэтому параметром состояния газа служит только абсолютное давление, которое и входит во все термодинамические зависимости.
. Поэтому параметром состояния газа служит только абсолютное давление, которое и входит во все термодинамические зависимости.
Удельный объем вещества представляет собой объем единицы массы вещества, т.е. это величина равная отношению объема к его массе 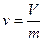 где
где 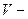 объем вещества;
объем вещества; 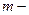 масса вещества. Величина обратная удельному объему называется плотностью вещества.
масса вещества. Величина обратная удельному объему называется плотностью вещества.
В технической термодинамике в качестве рабочего тела принимается идеальный газ — условное газообразное вещество, силами взаимодействия между молекулами которого пренебрегают. Если реальные газы сильно разряжены, их свойства близки к свойствам идеального газа. К основным законам идеальных газов относятся: закон Бойля-Мариотта, Гей-Люсака и Шарля, Авогадро.
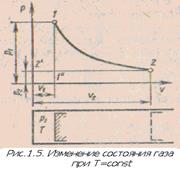 Закон Бойля — Мариотта. При постоянной температуре удельные объемы данного газа обратно пропорциональны его абсолютным давлениям. В координатах давление – объем процесс изменения состояния газа при постоянной температуре изображается гиперболой (рис.1.5). Так как в каждой точке этой кривой температура газа одинакова, то кривая называется изотермой. Используя данный закон для точек, соответствующих началу и концу процесса получим
Закон Бойля — Мариотта. При постоянной температуре удельные объемы данного газа обратно пропорциональны его абсолютным давлениям. В координатах давление – объем процесс изменения состояния газа при постоянной температуре изображается гиперболой (рис.1.5). Так как в каждой точке этой кривой температура газа одинакова, то кривая называется изотермой. Используя данный закон для точек, соответствующих началу и концу процесса получим
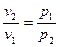 при
при 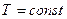 (1.1)
(1.1)
где индексы 1 и 2 относятся соответственно к начальному и конечному состоянию газа в процессе его расширения или сжатия. Из выражения (1.1) следует, что 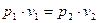 или
или 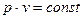 (1.2)
(1.2)
Закон Гей-Люссака- объем данной массы газа при постоянном давлении изменяется линейно в зависимости от температуры. Процесс в координатах давление – объем изображается линией, параллельной оси абсцисс (рис.1.6). Эта линия называется изобарой. Уравнение для начального и конечного состояния
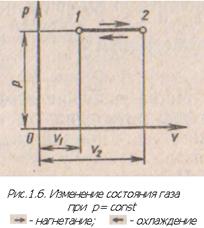
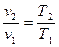 при
при 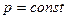 (1.3) Из уравнения (1.3) следует, что
(1.3) Из уравнения (1.3) следует, что 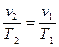 или
или 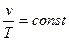 (1.4)
(1.4)
Таким образом, при постоянном абсолютном давлении удельные объемы идеального газа прямо пропорциональны его абсолютным температурам:
Закон Шарля. При постоянном объеме данной массы газа абсолютные давления идеального газа прямо пропорциональны его абсолютным температурам: 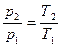 при
при 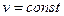 (1.5)
(1.5)
Выражение (1.5) можно записать в следующем виде: 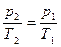 или
или 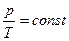 (1.6)
(1.6)
Закон Авогадро. В равных объемах разных идеальных газов при одинаковых температуре и давлении содержится равное число молекул — число Авогадро ( 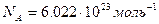 ). Количество вещества- это отношение числа молекул в данном теле к числу атомов в 0,012 кг углерода:
). Количество вещества- это отношение числа молекул в данном теле к числу атомов в 0,012 кг углерода: 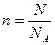 где
где 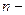 число молекул в данном теле. Количество вещества измеряют в молях. Моль — это количество вещества, содержащее столько же молекул, сколько содержится атомов в 0,012 кг углерода. В системе единиц (СИ) под молем понимают количество вещества в граммах, численно равное его молекулярной массе (
число молекул в данном теле. Количество вещества измеряют в молях. Моль — это количество вещества, содержащее столько же молекул, сколько содержится атомов в 0,012 кг углерода. В системе единиц (СИ) под молем понимают количество вещества в граммах, численно равное его молекулярной массе ( 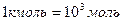 ). Молярной массой вещества называется величина, равная отношению массы вещества к его количеству
). Молярной массой вещества называется величина, равная отношению массы вещества к его количеству 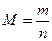 где
где 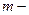 масса вещества,
масса вещества, 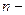 количество вещества.
количество вещества.
Молярная масса выражается в 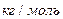 . Объем одного киломоля при нормальных условиях
. Объем одного киломоля при нормальных условиях
Для всех газов равен 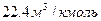 . Отсюда следует, что можно легко определить удельный объем и плотность любого газа при нормальных условиях (
. Отсюда следует, что можно легко определить удельный объем и плотность любого газа при нормальных условиях ( 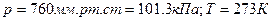 ) по формулам
) по формулам 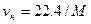 :
: 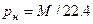
Рассмотренные законы Бойля-Мариотта, Гей-Люсака и Шарля устанавливают связь только между двумя из трех основных параметрами газа давлением, удельным объемом и температурой при условии, что значение третьего параметра остается постоянным. В технике обычно совершаются процессы, когда изменяются все три параметра. Уравнения, которые устанавливают зависимость между всеми параметрами газа, называются уравнениями состояния, которое имеет вид
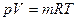 (1.7).
(1.7).
Данное уравнение (1.7) состояния газа называется уравнением Клапейрона. В этом уравнении постоянная 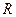 (
( 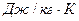 ), имеющая для каждого газа определенное численное значение, называется газовой постоянной и ее значения можно вычислить, зная параметры любого состояния газа. Газовая постоянная становится универсальной, т.е. одинаковой для всех газов, если количество газов выразить в кмолях (объем 1-го кмоля любого газа
), имеющая для каждого газа определенное численное значение, называется газовой постоянной и ее значения можно вычислить, зная параметры любого состояния газа. Газовая постоянная становится универсальной, т.е. одинаковой для всех газов, если количество газов выразить в кмолях (объем 1-го кмоля любого газа 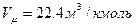 ), которое будет составлять
), которое будет составлять 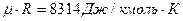 В результате уравнение состояния для 1-го кмоля газа можно представить в виде
В результате уравнение состояния для 1-го кмоля газа можно представить в виде 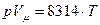 (1.9). Из этого уравнения, зная численное значение относительной молекулярной массы, можно определить газовую постоянную любого газа.
(1.9). Из этого уравнения, зная численное значение относительной молекулярной массы, можно определить газовую постоянную любого газа.
Таким образом, по физическому смыслу газовая постоянная 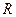 соответствует работе расширения 1-го кг газа при нагревании его на один кельвин в условиях постоянного давления. Аналогичный смысл, но применительно к 1-му кмолю газа имеет и постоянная Менделеева, т.е. универсальная газовая постоянная есть работа 1-го кмоля газа при нагревании его на 1 кельвин в условиях постоянного давления.
соответствует работе расширения 1-го кг газа при нагревании его на один кельвин в условиях постоянного давления. Аналогичный смысл, но применительно к 1-му кмолю газа имеет и постоянная Менделеева, т.е. универсальная газовая постоянная есть работа 1-го кмоля газа при нагревании его на 1 кельвин в условиях постоянного давления.
Газовые смеси. На практике обычно приходится иметь дело не с однородными газами, а с их смесями. Примером газовой смеси может служить отработавшие газы ДВС, которые являются механической смесью газов, включающей углекислый газ, азот, кислород, окись углерода и водяной пар.
Для проведения тепловых расчетов, связанных с газовыми смесями, необходимо знать состав газовой смеси. Состав смеси задается массовыми или объемными долями. Массовая доля данного  газа есть отношение его массы к массе всей смеси, т. е.
газа есть отношение его массы к массе всей смеси, т. е.
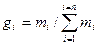
где 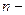 количество компонентов в газовой смеси.
количество компонентов в газовой смеси.
Объемная доля данного 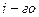 газа есть отношение его приведенного объема (объема газа, приведенного к температуре
газа есть отношение его приведенного объема (объема газа, приведенного к температуре 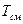 и давлению
и давлению 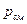 смеси) к объему занимаемому всей газовой смесью, т. е.
смеси) к объему занимаемому всей газовой смесью, т. е. 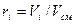
Так как газовая смесь, состоящая из отдельных однородных идеальных газов, представляет собой другой идеальный газ, то для него справедливы характеристические уравнения состояния.
Теплоемкость газов. Для определения количества теплоты, подводимой к газу или отводимой от него при осуществлении того или иного процесса, необходимо знать теплоемкость этого газа. Теплоемкость характеризует способность вещества воспринимать теплоту при нагревании или отдавать ее при охлаждении.
Количество теплоты, поглощаемое телом при нагревании на 1 кельвин, называется теплоемкостью, а теплоемкость единицы массы вещества называется удельной теплоемкостью.
В связи с тем, что теплоемкость газа зависит от температуры, различают истинную и среднюю теплоемкость.
Под удельной истинной теплоемкостью понимают отношение бесконечно малого количества теплоты, подводимой к единице количества газа, к вызываемому при этом
бесконечно малому повышению его температуры. Численное значение истинной теплоемкости газа определяется по таблицам или графически в зависимости от температуры газа.
Удельной средней теплоемкостью называют количество теплоты, необходимое для нагревания единицы количества газа на один кельвин в среднем за рассматриваемый интервал изменения температуры газа (от 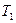 до
до 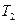 ).
).
Характерными условиями нагревания являются постоянство объема и давления газа. Теплоемкости при постоянном объеме обозначают 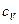 ,
, 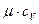 , а при постоянном давлении -
, а при постоянном давлении - 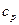 ,
, 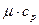 . Разность между молярной теплоемкостью
. Разность между молярной теплоемкостью 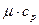 при постоянном давлении и молярной теплоемкостью
при постоянном давлении и молярной теплоемкостью 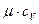 при постоянном объеме для всех газов одинакова и равна
при постоянном объеме для всех газов одинакова и равна 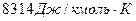 . По физическому смыслу 8314 – это количество теплоты, эквивалентное работе одного кмоля любого газа при нагревании его на 1 К при любом постоянном давлении.
. По физическому смыслу 8314 – это количество теплоты, эквивалентное работе одного кмоля любого газа при нагревании его на 1 К при любом постоянном давлении.
В теплотехнических расчетах широко используется отношение теплоемкостей, обозначаемое k и называемое показателем адиабаты, который определяется по формуле
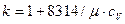
Дата добавления: 2016-03-05; просмотров: 1998;
