Схема простейшего регулятора межэлектродного зазора
Обязательным элементом любого электроэрозионного станка является автоматический регулятор МЭЗ (межэлектродный зазор).
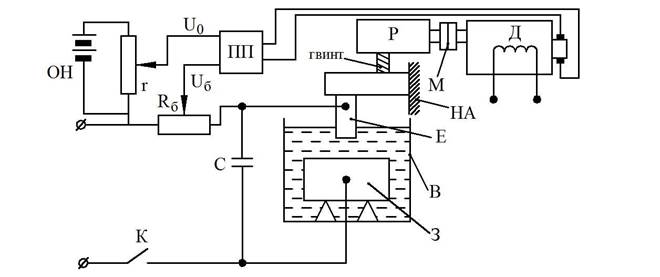
В - ванна
Rб- опір баластний;
М - муфта;
Р - редуктор;
Д - двигун;
ПП - підсилювач перетворювач;
r - потенціометр;
ОН - джерело живлення (додаткове джерело живлення);
Е - електрод;
З - заготовка;
НА напрямна арматура
С - конденсатор.
Принцип работы схемы. На якорь двигателя привода электрода подается разность двух напряжений Uб, на баластном сопротивлении Rб - источника тока, и напряжения Uo, снимаемого с дополнительного источника ОН потенциометром r. При Uб=Uо якорь будет неподвижен. Величину скорости электрода можно определить из выражения:
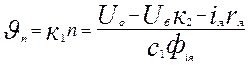 (2)
(2)
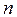 - число оборотов двигателя;
- число оборотов двигателя;
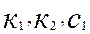 - постоянные коэффициенты;
- постоянные коэффициенты;
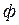 - поток возбуждения магнитный;
- поток возбуждения магнитный;
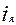 - ток якоря;
- ток якоря;
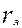 - сопротивление якоря.
- сопротивление якоря.
Для постоянного момента нагрузки 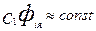 .
.
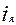 ,
, 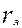 из-за маленького
из-за маленького 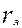 можно пренебречь. В этом случае можем записать:
можно пренебречь. В этом случае можем записать:
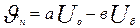 (3)
(3)
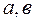 - постоянные коэффициенты.
- постоянные коэффициенты.
Если от напряжения перейти к зазору можем записать:
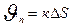 (4)
(4)
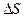 - отклонение величины зазора от заданного значения.
- отклонение величины зазора от заданного значения.
1) Регуляторы, реализующие подобный закон называются пропорциональными или П-регуляторами.
2) Кроме пропорциональных регуляторов существуют регуляторы, реализующие иные законы - интегральные регуляторы.
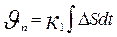 (5)
(5)
3) пропорционально интегральный регулятор (П-И-регулятор) реализует закон:
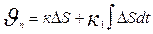 (6)
(6)
4) пропорционально интегральный дифференциальный регулятор (П-И-Д-регулятор)
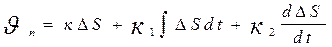 (7)
(7)
Реализовать этот регулятор очень сложно. Но он определяет наличие экстремума (за счет дифференциала).
Наиболее эффективным является закон регулятора ПИД. Производна отклонения отражает тенденцию изменения регулируемой величины. Величина и знак производной по отклонению несут информацию о том, куда и насколько отклоняется регулируемая величина через некоторое время. Регуляторы с воздействием по производной могут «предвидеть» возможное отклонение регулируемой величины и заблаговременно их устранить.
При исследовании систем управления, регулирования электроэрозионных станков важно различать в них переходные и установившиеся процессы.
Переходные процессы возникают при изменении задающего управляющего или возмущающего воздействия. В устойчивой системе по истечении времени регулирования устанавливается равновесное состояние между управляемой величиной и воздействиями. Это состояние обычно называется установившимся процессом. В САУ и САР как в замкнутой динамической системе возможны 4 вида протекания переходного процесса.
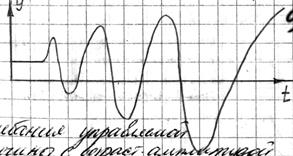
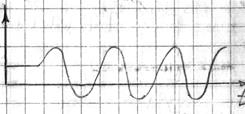
колебания управляемой колебания управляемой
величины с возрастающей величины с постоянной
амплитудой амплитудой
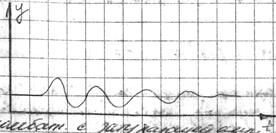

колебания с затухающей безколебательное или
амплитудой апериодическое возвра-
щение управляющей
величины к заданному
значению
Оценка качества САУ (САР) в электроэрозионных станках чаще всего производится по переходной характеристике – по величине перерегулирования 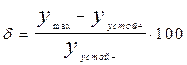 (8) - процент перерегулирования и времени переходного процесса tp.
(8) - процент перерегулирования и времени переходного процесса tp.
Рассмотрим процессы регулирования, происходящие в различных типах регуляторов.
1) П-регулятор
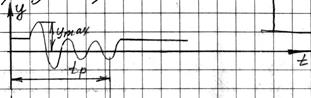
2) Интегральный регулятор
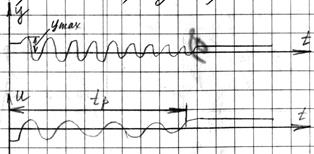
3) Комбинация (П-И регулятор)
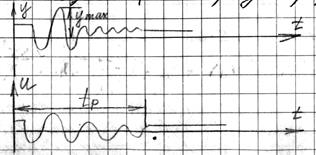
4) Пропорционально дифференциальный регулятор (П-И-Д регулятор)

Автоматическая система электроэрозионных станков работает, как правило, при непрерывн о изменяющихся сигналах управления и возмущения, поэтому для анализа их работы используется аппарат дифференциальных уравнений. Элементы систем автоматики, описываемые линейными дифференциальными уравнениями и системы состоящие из этих элементов называются линейными. Если же работа хотя бы одного элемента описывается нелинейным дифференциальным уравнением, то и вся система является нелинейной.
Рассмотрим линейные системы.
Любая линейная система управления может быть представлена в виде совокупности отдельных простых звеньев, описываемых простыми дифференциальными уравнениями. Выделение звеньев должно быть произведено так, чтобы состояние каждого звена, заменяющего элемент системы определялось одной переменной (  ). Кроме того звенья по возможности должны быть достаточно простыми, чтобы их можно было описать дифференциальными уравнениями не выше второго порядка
). Кроме того звенья по возможности должны быть достаточно простыми, чтобы их можно было описать дифференциальными уравнениями не выше второго порядка
Для каждого элемента в замкнутой системе имеется входная и выходная величина. Выходная величина как в переходном так и в установившемся процессе зависит от входной.

Принципиальная схема элемента
Математически зависимость между входными и выходными величинами может быть представлена дифференциальным уравнением, которое можно получить опытным путем или вывести теоретически при некоторой идеализации процессов, происходящих в элементе.
Рассмотрим некоторые наиболее часто встречающиеся элементы, входящие в состав автоматических систем.
1)  (9)
(9)
Звено типа статическая связь. При внезапном изменении входной величины выходная изменяется без запаздывания. Пример - редуктор, потенциометр.
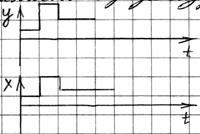
2) Дифференцирующее звено 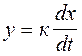 (10)
(10)
Звено типа скоростная связь. У этих звеньев выходная величина изменяется пропорционально скорости изменения входной величины (трансформатор).
3) 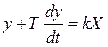 - апериодическое звено (11)
- апериодическое звено (11)
При внезапном изменении входной величины Х, выходная величина y нарастает по экспоненциальному закону, стремясь к установившемуся значению

Пример (катушка):
входная - U;
выходная - магнитный поток
конденсатор заряжен через активное сопротивление;
Х-U источника;
Х-U на конденсаторе;
Т- const времени, носящая размерность времени.
4) 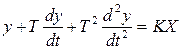 -колебательное звено(12)
-колебательное звено(12)
В этом звене при внезапном изменении входной величины Х, выходная (y) будет совершать затухающие синусоидальный колебания.
Пример: конденсатор, заряжаемый через индуктивность и сопротивление: Х-Uисточн; y-U на конденсаторе; маятник; Х - усилие; y - угол поворота.
В теории автоматического регулирования широкое распространение получила форма записи дифференциальных звеньев при помощи передаточных функций. Формально они представляют собой символичную запись дифференциального уравнения, однако, эти функции могут быть определены только путем преобразования вещественных функций в функции комплексной переменной, т.е. изображениями по Лапласу. Передаточная функция определяется как отношение изображений выходной и входной величин при нулевых начальных условиях. Передаточные функции, записанные с помощью комплексной переменной, полностью совпадают с выражениями, полученными из дифференциальных уравнений с применением оператора дифференцирования 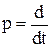 .
.
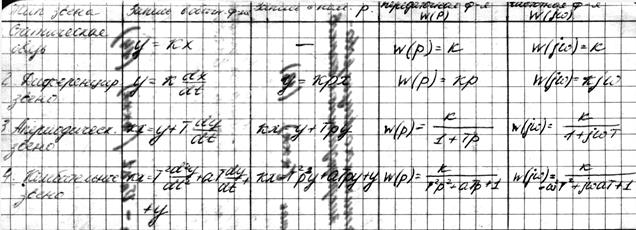
| Тип звена | Запись в обычной форме | Запись с помощью p | Передаточная функция W(p) | Частотная функция W(jω) |
| Статическая связь | ||||
| Диференциальное звено | ||||
| Апериодическое звено | ||||
| Колебательное звено |
| <== предыдущая лекция | | | следующая лекция ==> |
| ЭПИЛЕПТИЧЕСКИЙ СТАТУС | | | Мирное урегулирование. |
Дата добавления: 2016-03-05; просмотров: 1505;
