Кинематика автомобильного дифференциала
При помощи дифференциального механизма (рис.11.6) в автомобилях осуществляется передача вращательного движения от двигателя к ведущим колёсам. При повороте дифференциальный механизм распределяет мощности между ведущими колёсами таким образом, чтобы их обороты согласовывались с условиями движения.
Дифференциальный механизм состоит из центральных конических колёс 3 и 4, конического колеса – сателлита 5 и водила 2. Водило выполнено в виде конического колеса и передача вращения водилу осуществляется от карданного вала 1 при помощи обычной конической передачи 1 – 2. На основании (11.2):
(11.4)
Формула (11.4) связывает обороты водила n2 и обороты левого и правого колёс. Число оборотов n2 является известным. Если машина движется прямолинейно, то равенству к (11.4) добавляется n3=n4. При повороте к равенству (11.4) добавляется:
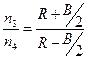(11.5)
Равенство (11.4) и (11.5) позволяют получить определённость решения и найти n3 и n4 .
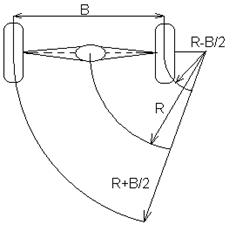
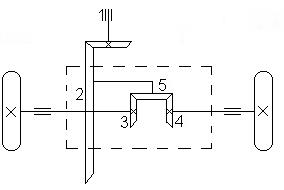
Рис.11.6
Планетарные механизмы
Если у дифференциального механизма центральное колесо 1 сделать неподвижным и тем самым отнять одну степень подвижности, то можно получить зубчатый механизм с одной степенью подвижности (рис.11.7).
Зубчатые механизмы со степенью подвижности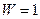 
, у которых геометрические оси некоторых колёс перемещаются, называются планетарными механизмами.
Найдём передаточные отношения. Рассматривая планетарный механизм как частный случай дифференциального механизма и полагая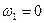 
, можно применить формулу (11.3). Получим:
= 
.
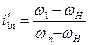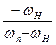Обратное передаточное отношение
,
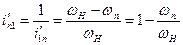где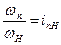 
- передаточное отношение от вала любого колеса n к валу водила H.
Следовательно,
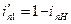или 
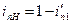(11.6)
Отметим, что к формуле (10.6) под цифрой 1 обозначено неподвижное колесо. Это необходимо учитывать и корректировать формулу при решении задач.
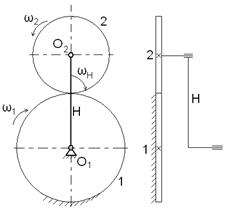
Рис.11.7
Пример 11.4
Определить передаточное отношение планетарного механизма (рис.11.8).
Дано: z1=100, z2=99,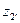 
=100, z3=101.
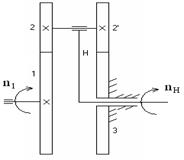
Рис.11.8
Решение:
По формуле (11.6) определим передаточное отношение (учтём, что здесь неподвижным является колесо 3):
Как видно, передаточное отношение здесь очень мало. Вал 1 вращается в 10 000 раз медленнее, чем вал водила. Для осуществления такого малого передаточного отношения при помощи обычного зубчатого механизма необходимо было бы сделать его многоступенчатым, что потребовало бы большого количества колес. Однако необходимо отметить, что при таких передаточных отношениях планетарный механизм может надежно работать только в сторону уменьшения числа оборотов ведомого вала по сравнению с ведущим, т. е. может передавать движение от водила к колесу. При передаче движения в сторону увеличения числа оборотов механизм при таких передаточных отношениях обладает очень низким к. п. д. и даже может быть самотормозящим, т. е. не может даже двигаться. Поэтому при очень малых передаточных отношениях планетарные передачи применяются только в маломощных механизмах, работающих в течение небольших промежутков времени (например, в приборах дистанционного управления). Большим достоинством планетарных механизмов, помимо возможности достижения больших передаточных отношений, является соосность ведущего и ведомого валов лёгкость и компактность конструкции.
Пример 11.5
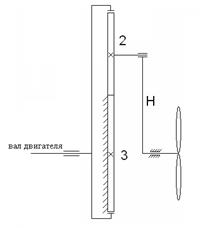
Определить передаточное отношение планетарного механизма (рис.11.9) от вала двигателя 1 к валу винта самолёта H и число оборотов винта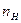 
, если число оборотов двигателя n1=3000 об./мин., а количество зубьев зубчатых колёс равно: z1=66 , z2=18 , z3=30.
Решение:
Передаточное отношение планетарного механизма:
Число оборотов винта:
Рис.11.9
Дата добавления: 2016-03-05; просмотров: 1940;