В целях энергосбережения
На небольших объектах значительного энергосбережения можно добиться за счет применения возобновляемых источников энергии. Наиболее приспособленными возобновляемыми источниками энергии являются Солнце, ветер и биотопливо[24]. Рассмотрим методические положения практического применения этих источников.
10.1. Автономные солнечные
электростанции
Задачу использования солнечной электростанции для автономного электроснабжения небольших потребителей можно сформулировать следующим образом: необходимо обеспечить электроснабжение потребителя, имеющего случайный график нагрузок, от источника энергии случайной мощности при минимальных затратах, при ограничении – электроснабжение на основе солнечной электростанции должно быть не менее надежно, чем традиционное.
Суточное электропотребление какого-либо абстрактного объекта можно представить графиком (рисунок 10.1).
Для удовлетворения потребности в электроэнергии можно либо использовать источник электроэнергии мощностью, обеспечивающей суточное энергопотребление (если позволяет график нагрузки), либо использовать источник меньшей мощности, но с аккумулированием энергии в периоды провала нагрузки и с отдачей аккумулированной энергии в часы пиковой нагрузки. Так как стоимость аккумуляторов априорно меньше стоимости фотоэлектрических преобразователей, и солнечное излучение отсутствует в ночные часы, то второй вариант в соответствии с поставленной задачей будет предпочтительнее.
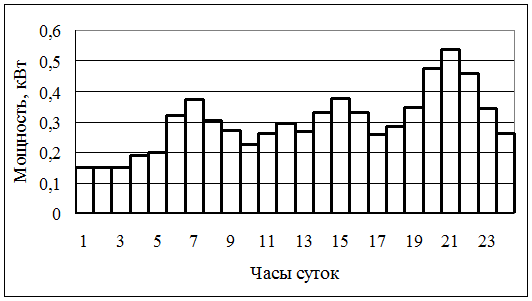
Рисунок 10.1 График нагрузки абстрактного
объекта электропотребления
Если мощность источника энергии постоянна, то, при аккумулировании энергии в периоды провалов, генерируемую мощность можно выбрать из условия /6, 7/:
∑(NГ – NПj) t1j ηA = ∑( NПi – NГ) t2i (10.1)
где: NГ – генерируемая мощность, кВт;
N1j – мощность потребителя в j-тый период, меньшая, чем генерируемая мощность, кВт;
N2i – мощность потребителя в i-тый период, большая, генерируемая мощность, кВт;
t1j – продолжительность j-того периода, час;
t2i – продолжительность i-того периода, час;
ηA – к.п.д. аккумулятора энергии.
В уравнении (10.1) левая часть представляет собой избыточную энергию, которая может быть аккумулирована. К.п.д. аккумулятора учитывает, что в последующем в пиковую нагрузку можно выдать только часть аккумулированной энергии.
Уравнение (10.1) является трансцендентным и его следует решать графически относительно генерируемой мощности. На рисунке 10.2 показан пример такого решения для приведенной абстрактной нагрузки для летних месяцев при ηA = 0,7 и среднегодовом поступлении солнечной энергии в этот период на территории Ростовской области.
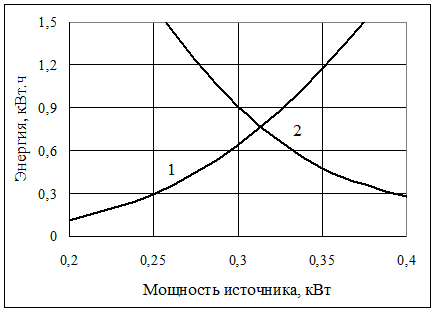
Рисунок 10.2. Графическое решение уравнения (10.1)
1 – левая часть, 2 – правая часть
В приведенном примере минимальная мощность источника энергии должна быть равной 0,32 кВт.
Для удовлетворения ограничения целевой функции необходимо учитывать особенность поступления солнечной энергии, которая определяет мощность электроэнергии, генерируемой фотоэлектрическими преобразователями при случайной интенсивности солнечного излучения. С учетом этого вероятностью энергообеспечения будет вероятность того, что энергии солнечного излучения будет достаточно для удовлетворения потребностей в получаемой электроэнергии. Минимальное значение мощности батареи фотоэлектрических преобразователей при этом можно определить из равенства /6, 7/:
∑(NФj – N1j) t1j ηA = ∑( N2i – NФi) t2i (10.2)
где: NФj – мощность батареи фотоэлектрических преобразователей в j-тый период, превышающая мощность потребителя в этот же период, кВт;
NФi – мощность батареи фотоэлектрических преобразователей в i-тый период, меньшая мощности потребителя в этот же период, кВт.
Учитывая, что мощность фотоэлектрического преобразователя определяется из условия
NФ = NС FФ ηФ (10.3)
уравнение (10.2) можно записать в следующем виде:
∑(NСj FФ ηФ – N1j) t1j ηA = ∑(N2i – NСi FФ ηФ) t2i (10.4)
Здесь: NСj – удельная мощность солнечного излучения в j-тый период, кВт/м2;
FФ – площадь батареи фотоэлектрических преобразователей, м2;
ηФ – к.п.д. батареи фотоэлектрических преобразователей.
Уравнение (10.4) относительно площади батареи фотоэлектрических преобразователей также решается графически. На рисунке 10.3 показан пример такого решения для прежней нагрузки при следящей системе батареи фотоэлектрических преобразователей без концентраторов. Полученная в результате этого площадь батареи фотоэлектрических преобразователей равна 58м2, что обеспечивает вероятность энергообеспечения не менее 0,9. Как видно с увеличением вероятности энергообеспечения площадь батареи фотоэлектрических преобразователей растет.
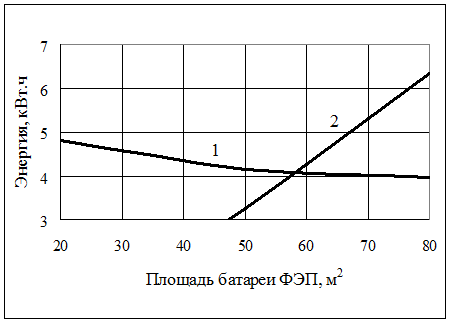
Рисунок 10.3. Решение уравнения (10.4)
при вероятности энергообеспечения 0,9
1 – левая часть, 2 – правая часть
Как видно из рисунка 10.3 мощность ФЭП несколько выше мощности топливной электростанции (см. рисунок 10.2). Это объясняется тем, что в утренние и вечерние часы фотоэлектрические преобразователи не могут обеспечить номинальную мощность. Определенная таким образом площадь батареи фотоэлектрических преобразователей будет достаточной для зарядки аккумуляторов и питания нагрузки с заданной вероятностью энергообеспечения в течение расчетного периода. То есть, расчетная площадь фотоэлектрических преобразователей способна в летнее время обеспечить заданную нагрузку в течение 1990 часов, что составляет 0,9 от расчетного периода. В остальное время (220 часов) нагрузка будет удовлетворяться не менее чем на 50%. Емкость аккумуляторов при этом можно определить из соотношения /6, 7/:
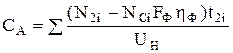 (10.5)
(10.5)
где СА – емкость аккумуляторной батареи, А.ч.;
UН – номинальное напряжение потребителя, В.
Таким образом, для данного примера (при вероятности энергообеспечения 0,9) площадь фотоэлектрических преобразователей должна быть 60 м2, а емкость батареи аккумуляторов (при напряжении потребителей UН = 220 В) 20 А.ч, или общая емкость аккумуляторов 380 А.ч.
10.2. Методика массовых
расчетов автономных солнечных электростанций
В процессе инженерных расчетов определяются оптимальные параметры автономных энергетических комплексов, приводящие к их наиболее высокой конкурентоспособности. Для проведения расчетов параметров автономных солнечных электростанций для массовых заказчиков желательно иметь инженерные методы, позволяющие получать искомые оптимальные параметры более простыми способами без поиска экстремумов целевых функций. В основе таких расчетов могут быть различные эмпирические функции (например, функции уравнений линейной регрессии), графики и таблицы, описывающие зависимости оптимальных параметров от влияющих факторов. Получить такие зависимости можно путем описания движения оптимального параметра в области изменения влияющих на него факторов.
В таблице 10.1 приведены оптимальные параметры автономной системы электроснабжения удаленных объектов на основе использования энергии солнечного излучения, а на рисунках 10.4 и 10.5 приведены графики этих параметров в зависимости от средней потребляемой мощности электроприемников и требуемой надежности электроснабжения /6, 7/.
Таблица 10.1
Расчетные параметры автономного энергетического комплекса
сезонно работающих объектов
| Средняя нагрузка объекта, Вт | Площадь ФЭП (м2) при вероятности энергообеспечения: | Емкость аккумуляторной батареи (А.ч) при вероятности энергообеспечения | ||||||||
| 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | 0,5 | 0,6 | 0,7 | 0,8 | 0,9 | |
| 22,3 28,0 33,0 38,5 43,5 | 26,0 32,5 38,5 44,7 51,0 | 29,0 35,8 42,5 49,3 56,7 | 31,2 38,3 46,0 53,5 61,0 | 35,5 44,5 53,0 62,0 71,0 |
Для проведения расчетов можно пользоваться уравнениями регрессии
F = 0,066х1 + 596х2 + 0,168х1х2 – 0,0002х12 – 894х22 +
+ 1,9Е-07х13 + 435х23 – 131 (10.6)
СА = 0,449х1 – 370х2 + 0,786х1х2 – 0,0013х12 – 216х22 +
+ 1,9Е-06х13 + 288х23 + 303 (10.7)
Здесь: х1 – среднесуточная нагрузка, Вт;
х2 – заданная вероятность энергообеспечения.
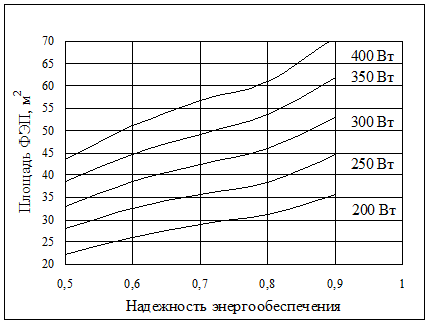
Рисунок 10.4. Размеры батареи фотоэлектрических преобразователей
в зависимости от нагрузки и надежности энергообеспечения
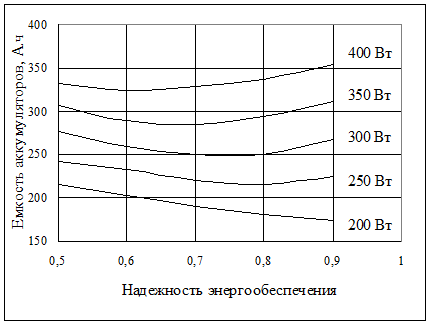
Рисунок 10.5. Емкость аккумуляторных батарей в зависимости от нагрузки и надежности энергообеспечения
В случае применения концентраторов солнечного излучения и систем слежения площадь батарей фотоэлектрических преобразователей уменьшается и определяется по формуле:
FУТ = kУТ F (10.8)
где FУТ – уточненное значение площади батарей фотоэлектрических преобразователей, м2;
F – площадь батареи фотоэлектрических преобразователей по формуле (5.10), м2;
kУТ – коэффициент уточнения.
Значения коэффициентов уточнения площади батарей фотоэлектрических преобразователей приведены в таблице 10.2 /6/.
Таблица 10.2
Значения коэффициентов уточнения
| Вариант | Коэффициент уточнения |
| 1. Система точного слежения без концентраторов 2. Параболические концентраторы с периодическим слежением и коэффициентом концентрации: до 3; 3 – 5; больше 5. 3. Концентраторы первого порядка с системой точного слежения и коэффициентом концентрации: до 3; больше 3. | 0,75 0,65 0,55 0,50 0,65 0,55 |
10.3. Мероприятия по повышению эффективности
автономных солнечных электростанций
Интенсивность солнечного излучения зависит от взаимной ориентации Солнца и солнечного коллектора (рисунок 10.6). На рисунке 10.6 азимутальный угол Солнца равен нулю, то есть Солнце по отношению к наблюдателю, находящемуся в северном полушарии, расположено строго на юге.

Рисунок 10.6. Параметры ориентации
солнечного коллектора в северном полушарии Земли
α – угол солнцестояния, β – угол наклона коллектора, γ – азимутальный угол коллектора, γС – азимутальный угол Солнца.
Очевидно, значительного увеличения поступления энергии солнечного излучения на фотоприемник можно достичь путем оптимальной ориентации батареи фотоэлектрических преобразователей. При этом следует учитывать, что прозрачность атмосферы, определяющая интенсивность прямого солнечного излучения, изменяется в течение суток и года. Так, например, на территории Ростовской области по статистике в первой половине светового дня атмосфера более прозрачна, а во второй половине дня появляется облачность. На основании этого можно предположить, что фиксированные преобразователи должны иметь отрицательный азимутальный угол, то есть, должны быть повернуты в сторону востока на какой-то угол. Изменение азимутального угла повлечет и изменение угла наклона, так как Солнце, не достигнув полуденного положения, будет иметь меньший угол солнцестояния.
Плотность солнечного излучения, поступающего на солнечный коллектор, определяется по формуле /6/:
Sк = S[Sпi cosai cos(gс i - g) sinb + Sгi cosb] (10.9)
где: Sк - суммарная за год плотность солнечного излучения на коллектор с параметрами ориентации γ и β, Вт/м2;
Sпi - плотность солнечного излучения на перпендикулярную к нему площадку за i-тый промежуток времени, Вт/м2;
ai - средний угол солнца над горизонтом в i-тый период времени, град;
gсi - средний азимут солнца за i-тый период времени, град.
Метеорологические станции имеют наиболее полную информацию о плотности солнечного излучения на горизонтальную поверхность. Выразим Sп через Sг :
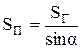 (10.10)
(10.10)
Тогда (10.9) будет иметь вид:
Sк = SSгi[ctgai cos(gсi - g) sinb + cosb] (10.11)
Как следует из (10.11), суммарная годовая плотность солнечного излучения на фиксированный коллектор зависит от двух параметров, g и b.
Оптимальное значение угла g определяется из равенства:
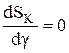 , при b = const ¹ 0 (10.12)
, при b = const ¹ 0 (10.12)
Проведя дифференцирование, получаем:
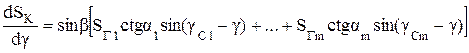 (10.13)
(10.13)
Воспользуемся тригонометрическим тождеством
sin(γCi – γ) = sinγCi cosγ - cosγCi sin γ (10.14)
Обозначив Ai = SГictgαi, разделив (10.13) на sinβ ≠ 0 и с учетом (10.14), получаем:
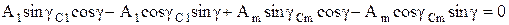 (10.15)
(10.15)
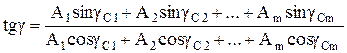 (10.16)
(10.16)
Или, проведя обратную подстановку, окончательно получаем:
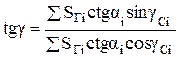 (10.17)
(10.17)
Как следует из (10.17), оптимальный азимутный угол ориентации солнечного коллектора не зависит от угла его наклона к горизонту.
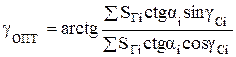 (10.18)
(10.18)
Оптимальный угол b определяется при γ = γопт из условия:
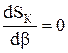 (10.19)
(10.19)
Выполнив дифференцирование, получаем:
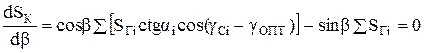 (10.20)
(10.20)
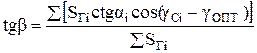 ; (10.21)
; (10.21)
 (10.22)
(10.22)
Анализируя (10.22), замечаем, что оптимальный угол наклона солнечного коллектора к горизонту зависит от его азимутального угла gопт. Отсюда последовательность оптимизации параметров ориентации солнечного коллектора должна быть следующей:
§ вычисляется оптимальный азимутальный угол солнечного коллектора по формуле (10.18);
§ вычисляется оптимальный угол наклона солнечного коллектора по формуле (10.22) при фиксированном оптимальном азимутальном угле.
В таблице 10.3 в качестве примера приведены расчетные и рекомендуемые на территории Ростовской области параметры ориентации фиксированных батарей фотоэлектрических преобразователей.
Таблица 10.3
Параметры ориентации
фиксированной батареи фотоэлектрических преобразователей
| Месяц | Азимутальный угол, град. | Угол наклона к горизонту, град. |
| Январь Февраль Март Апрель Май Июнь Июль Август Сентябрь Октябрь Ноябрь Декабрь | – 0,3 – 0,3 – 1,3 – 18,5 – 16,4 – 11,7 – 14,3 – 15,6 – 20,7 – 5,6 – 8,5 – 17,6 | 70,4 62,9 51,8 40,6 31,1 27,2 28,4 35,7 47,3 57,8 67,5 71,8 |
10.4. Системные
ветроэлектростанции
Системные ветроэлектростанции являются разгрузочными источниками энергии в централизованной сети электроснабжения. В соответствии с назначением, системные электростанции не нуждаются в аккумуляторах энергии, так как работают (разгружают традиционные электростанции) только тогда, когда имеется ветер достаточной мощности. В связи с этим системные электростанции рассчитываются по максимальной выработке электроэнергии за год в конкретном климатическом регионе.
Исходным расчетным параметром, определяющим мощность системной ветроэлектростанции, является рабочая скорость ветра. Заметим, что конкретная ветроустановка не может иметь один и тот же коэффициент использования энергии ветра при разных скоростях, так как ее аэродинамические параметры рассчитываются на определенную рабочую скорость ветра, являющейся номинальной. При увеличении скорости ветра больше рабочей, мощность, снимаемая с ветроколеса, остается постоянной. Таким образом, не смотря на увеличение мощности ветрового потока при увеличении его скорости, мощность ветроэлектростанции не увеличивается.
В любой климатической зоне имеются ветра с различной скоростью, включая и штиль. Каждая климатическая зона имеет характерный для нее ветровой кадастр, определяющий вероятность скорости ветра. Время действия ветра с определенной скоростью на основании данных ветрового кадастра можно определить следующим образом.
tV = v·T·p(v) (10.23)
где tV – время действия ветра со скоростью v, час;
T – число часов в году, час. Т = 8760 часов;
p(v) – вероятность ветра со скоростью v.
Если принять, что текущее значение скорости ветра является значением рабочей скорости, то энергия, передаваемая ветроколесом, равна:
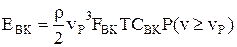 (10.24)
(10.24)
где ρ – плотность воздуха в ветровом потоке, кг/м3. Принимают ρ = 0,65 кг/м3;
vР – текущее значение рабочей скорости ветра, м/с;
Р(v ≥ vР) – вероятность того, что скорость ветра будет не меньше рабочей;
FВК – ометаемая площадь ветроколеса, м2;
СВК – коэффициент использования энергии ветра ветроколесом в номинальном режиме.
Вероятность того, что скорость ветра будет не меньше текущего значения рабочей скорости, равна сумме вероятностей скоростей ветра равных и больше рабочей:
 при vj ≥ vР
при vj ≥ vР
(10.25)
Р(v ≥ vР) = 0 при vj < vР
Расчет по формуле (10.24) с учетом (10.25) показывает, что максимальное значение передаваемой энергии будет у ветроколеса, рассчитанного на скорость ветра vР = 1,5vСР, где vСР – среднее значение скорости ветра для данной климатической зоны. При этом ветроустановка в течение примерно 3000 часов в году будет выдавать номинальную мощность, и в течение 1500 часов 50% номинальной мощности.
Зная рабочую скорость ветра, мощность системной ветроэлектростанции можно определить по формуле:
NВЭС = 0,65 vP3 FBK cBK ηВК ηСГ (10.26)
где ηВК – к.п.д. ветроколеса;
ηСГ – к.п.д. синхронного генератора.
Практически задаются желаемой мощностью ветроэлектростанции и рассчитывают ометаемую площадь ветроколеса и его диаметр. В заключении отметим, что ветроустановки мощностью более 100 кВт экономически эффективнее выполнять многоагрегатными, в которой мощность отдельной ветроустановки (агрегата) составляет 30 – 50 кВт.
10.5. Автономные
ветроэлектростанции
Дата добавления: 2016-03-05; просмотров: 1225;
