Задания для самостоятельного решения
► Для заданных дифференциальных уравнений подберите шаг разбиения в методе Эйлера, обеспечивающий абсолютную погрешность вычислений, не превышающую 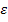 = 0,005:
= 0,005:
57. 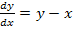 , при начальных условиях y(0) =1,5;
, при начальных условиях y(0) =1,5;
58. 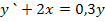 , при начальных условиях y(0) = 0,5;
, при начальных условиях y(0) = 0,5;
59. 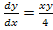 , при начальных условиях у(0)= 1;
, при начальных условиях у(0)= 1;
60. 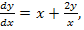 при начальных условиях у(1)= 2;
при начальных условиях у(1)= 2;
61. 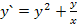 ,при начальных условиях у(2)= 4;
,при начальных условиях у(2)= 4;
62. 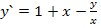 , при начальных условиях у(1) = 4;
, при начальных условиях у(1) = 4;
63. 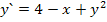 , при начальных условиях у(0)= 1;
, при начальных условиях у(0)= 1;
64. 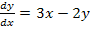 , при начальных условиях у(1) = 3;
, при начальных условиях у(1) = 3;
65. 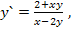 при начальных условиях у(1)= 2;
при начальных условиях у(1)= 2;
66. 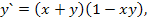 при начальных условиях у(0)= 1.
при начальных условиях у(0)= 1.
► Решить методом Эйлера дифференциальные уравнения. Вычисления провести с абсолютной погрешностью не превышающей 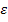 = 0,01:
= 0,01:
67. 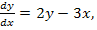
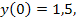
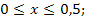
68. 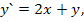
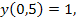
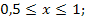
69. 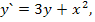
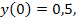
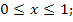
70. 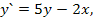
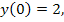
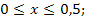
71. 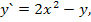
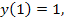
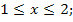
72. 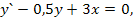
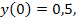
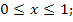
73. 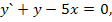
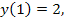
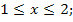
74. 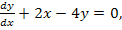
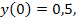
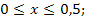
75. 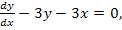
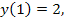
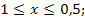
76. 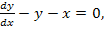
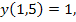
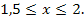
► Используя метод Эйлера, составить таблицу приближенных значений интеграла дифференциального уравнения уỹ = f(x, у), удовлетворяющего начальным условиям y(x0)=y0 на отрезке [а, Ь], принять шаг равным h = 0,1. Вычисления вести с четырьмя десятичными знаками. Аргумент тригонометрических функций выражен в радианах:
77. 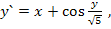
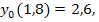
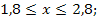
78. 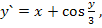
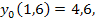
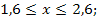
79. 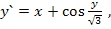
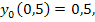
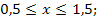
80. 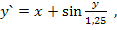
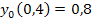 ,
, 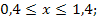
81. 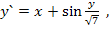
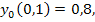
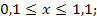
82. 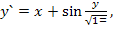
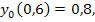
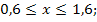
83. 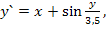
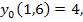
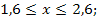
84. 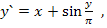
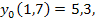
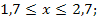
85. 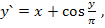
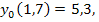
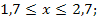
86. 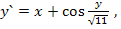
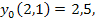
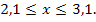
► Применяя метод Эйлера, численно решить дифференциальные уравнения с данными начальными условиями с шагом h и  :
:
87. 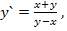
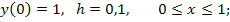
88. 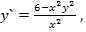
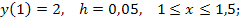
89. 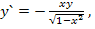
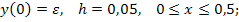
90. 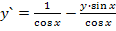 ,
, 
91. 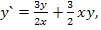
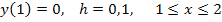 ;
;
92. 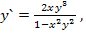
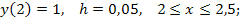
93. 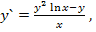
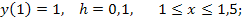
94. 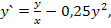
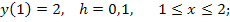
95. 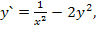
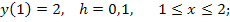
96. 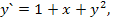
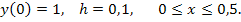
Дата добавления: 2016-03-04; просмотров: 1051;
