Дифференцирование сложной функции многих переменных
Для функции одной переменной производная сложной функции равна, грубо говоря, произведению производных соответствующих функций. Более точная формулировка правила вычисления производной сложной функции будет нами дана для ряда конкретных случаев ФНП. В общем случае дана функция 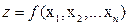 от
от 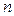 переменных, каждая из которых является функцией от
переменных, каждая из которых является функцией от 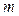 переменных, т. е.
переменных, т. е. 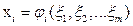 ,
,  .
.
Как всегда, начнем с функции двух переменных 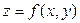 , в которой сами аргументы являются функциями двух других переменных. Пусть, например,
, в которой сами аргументы являются функциями двух других переменных. Пусть, например, 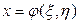 ,
, 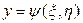 и надо вычислить частные производные
и надо вычислить частные производные 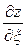 ,
, 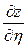 . Как разобраться в тех формулах, которые возникают в подобных ситуациях? Мы будем предполагать, что все функции дифференцируемы в рассматриваемых точках. Для функции запишем ее полное приращение
. Как разобраться в тех формулах, которые возникают в подобных ситуациях? Мы будем предполагать, что все функции дифференцируемы в рассматриваемых точках. Для функции запишем ее полное приращение 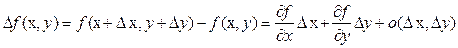 . Поделим обе части этого равенства на
. Поделим обе части этого равенства на 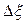 и перейдем в полученном соотношении к пределу при
и перейдем в полученном соотношении к пределу при 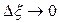 . Предел величины
. Предел величины 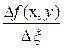 равен
равен 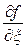 , если предел правой части существует. В правой части
, если предел правой части существует. В правой части 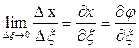 ,
, 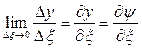 ,
, 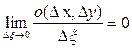 , следовательно, предел правой части существует и справедливо равенство
, следовательно, предел правой части существует и справедливо равенство 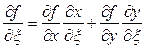 . Совершенно аналогично доказывается вторая формула
. Совершенно аналогично доказывается вторая формула 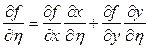 .
.
Вернемся к общему случаю 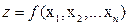 ,
, 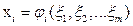 ,
,  . В этом случае
. В этом случае 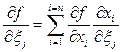 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| Система международного спортивного права | | | Главное окно Delphi |
Дата добавления: 2016-03-04; просмотров: 878;
