Уравнения Максвелла. Волновая природа света

В 1861 – 1862 гг Джеймс Максвелл предположил, что изменяющееся со временем магнитное поле обуславливает появление в пространстве поля электрического, независимо от присутствия в этом пространстве поля проводящего контура. Наличие контура лишь позволяет обнаружить существование в соответствующих точках пространства электрического поля. Причем возникающее таким образом электрическое поле, является вихревым, т.е. силовые лини такого электрического поля замкнуты.

В результате Максвеллом было обосновано существование электромагнитного поля, а электрическое и магнитное поля – являются частными случаями электромагнитного.

Основу теории образуют уравнения Максвелла.

Две пары уравнений Максвелла в дифференциальной и интегральной форме:

№ п/п	В дифференциальной форме	В интегральной форме

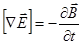
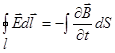
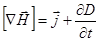
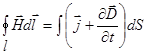
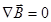
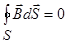
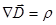
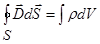
Где

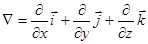- оператор Гамильтона (набла);

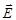- вектор напряженности электрического поля;

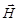- вектор напряженности магнитного поля;

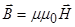- индукция магнитного поля;

μ – магнитная проницаемость;

μ₀ = 4π·10^-7 Гн/м – магнитная постоянная;

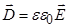- электрическая индукция (электрическое смещение);

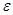- диэлектрическая проницаемость;

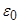= 8,85·10^-12 Ф/м – диэлектрическая постоянная;

j – плотность тока ( );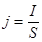

ρ — плотность свободных зарядов ( ).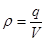

Формулировка уравнений.

1) Циркуляция вектора 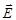по замкнутому контуру l, который является границей поверхности S, равна изменению потока магнитной индукции (производной по времени от магнитного потока), проходящего через поверхность S, взятому с обратным знаком.