Порядок применения обобщенного критерия Гурвица
1. Упорядочиваем матрицу игры таким образом, чтобы исходы каждой альтернативы располагались в порядке возрастания. При этом в одном столбце матрицы могут оказаться исходы, относящиеся к разным состояниям - это не существенно. В результате вместо "старой" матрицы игры Х мы получаем "новую" матрицу Y, где в каждой строке исходы располагаются от самого маленького до самого большого:
xi1, xi2,..., xij,..., xiM → yi1 ≤ yi2 ≤... ≤ yiq ≤... ≤ yiM
2. Рассчитываем суммы исходов по каждому столбцу новой матрицы Y:
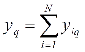
3. Рассчитываем сумму все исходов матрицы:
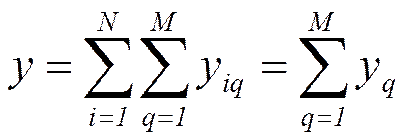
4. Далее коэффициенты λq определяются в зависимости от отношения ЛПР к неопределенности.
4.1. Если ЛПР оптимист, то коэффициент λq для любого q-го столбца определяется по формуле:
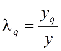
Поскольку для каждой альтернативы соблюдается условие:
yi1 ≤ yi2 ≤... ≤ yiq ≤... ≤ yiM
то y1 ≤ y2 ≤... ≤ yq ≤... ≤ yM
и, следовательно:
λ1 ≤ λ2 ≤ ... ≤ λq ≤ ... ≤ λM
То есть, чем лучше исход, тем больше удельный вес ему присваивается.
Кроме того, так как
 ,
,
то обеспечивается выполнение равенства:

Таким образом, полученные формальным путем коэффициенты отвечают необходимым условиям.
4.2. Если ЛПР пессимист, то определение коэффициентов немного сложнее. Мы должны обеспечить соблюдение условия: худшим исходам - большие веса. Это можно сделать, зеркально поменяв местами коэффициенты, рассчитанные для оптимистичного ЛПР:
а) при нечетном количестве состояний М:
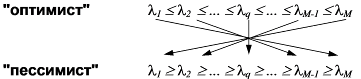
б) при четном количестве состояний М:

Формальная запись зависимости для расчета коэффициентов λq при пессимистично настроенном ЛПР выглядит следующим образом:
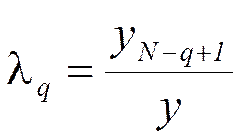
5. Теперь, имея все значения коэффициентов λq, можно рассчитать величину обобщенного коэффициента Гурвица для каждой i-й альтернативы:
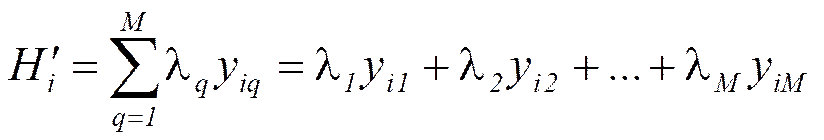
6. Оптимальной является стратегия, у которой наибольшее значение обобщенного критерия Гурвица:
Х* = Хk, H'k = max(H'i), i=1..N
Пример применения обобщенного критерия Гурвица
Применим обобщенный критерий Гурвица для поиска оптимального решения в условиях задачи из табл. 3 для оптимистически и пессимистически настроенного ЛПР.
Будем действовать в соответствии с изложенным выше алгоритмом.
1. Упорядочим матрицу игры, расположив исходы в порядке возрастания (табл. 5).
Таблица 5
Упорядоченная матрица игры Y (для примера).
| Альтернативы (Xi) | Номер столбца (q) | ||
| Х1 | 25 | 45 | 50 |
| X2 | 20 | 25 | 60 |
| yq = ∑yiq | 45 | 70 | 110 |
| y = ∑ yq | 225 | ||
| λqO оптимист | 0.20 | 0.31 | 0.49 |
| λqП пессимист | 0.49 | 0.31 | 0.20 |
2. Рассчитаем суммы yq по столбцам упорядоченной матрицы:
y1 = y11 + y21 = 25 + 20 = 45
y2 = y12 + y22 = 45 + 25 = 70
y3 = y13 + y23 = 50 + 60 = 110
3. Рассчитаем сумму всех исходов:
y = y1 + y2 + y3 = 45 + 70 + 110 = 225
4. Рассчитаем коэффициенты для каждого ЛПР.
4.1. коэффициенты для ЛПР оптимиста:
λ1 О = 45/225 = 0.2
λ2 О = 70/225 = 0.31
λ3 О = 110/225 = 0.49
4.2. коэффициенты для ЛПР пессимиста рассчитывать нет необходимости - главное, правильно поменять местами уже найденные коэффициенты:
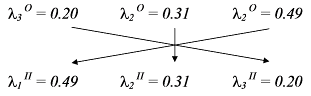
5. Рассчитать значения обобщенного критерия Гурвица для каждого проекта для каждого ЛПР:
5.1. ЛПР-оптимист
H'1O = λ1O y11 + λ2O y12 + λ3O y13 = 0.20×25+ 0.31×45 + 0.49×50 = 43.4
H'2O = λ1O y21 + λ2O y22 + λ3O y23 = 0.20×20+ 0.31×25 + 0.49×60 = 41.1
5.2. ЛПР-пессимист
H'1П = λ1 П y11 + λ2 П y12 + λ3 П y13 = 0.49×25+ 0.31×45 + 0.20×50 = 36.2
H'2 П = λ1 П y21 + λ2 П y22 + λ3 П y23 = 0.49×20+ 0.31×25 + 0.20×60 = 29.6
6. Сравнить полученные значения обобщенного коэффициента Гурвица. Оптимальными для каждого ЛПР являются проекты с максимальным значением критерия:
ЛПР-оптимист:
43.4 > 41.1 => H'1 О > H'2 О => X* = X1
ЛПР-пессимист:
36.2 > 29.6 => H'1 П > H'2 П => X* = X1
Здесь и для оптимистичного, и для пессимистичного ЛПР оптимальным по обобщенному критерию Гурвица является первый проект.
Благодаря тому, что в оценке учитываются все исходы, обобщенный критерий Гурвица лишен недостатка обычного критерия. Кроме того, формальный подход к расчету коэффициентов максимально снижает степень субъективности. ЛПР достаточно определить лишь общий характер своего отношения к неопределенности - оптимистичный или пессимистичный, тогда как при использовании обычного критерия требовалось еще и самому задать уровень оптимизма.
Мы рассмотрели шесть основных критериев, которые можно применять для принятия решений в условиях неопределенности. Если проанализировать то, как они построены, то можно заметить, что пять из них, по сути, отличаются между собой только разными весовыми коэффициентами, присваиваемыми исходам. Действительно, все критерии, кроме критерия Сэвиджа, могут быть описаны формулой:
Где
λj - удельный вес j-го значения исхода рассматриваемой i-й альтернативы,0 ≤ λj ≤ 1,
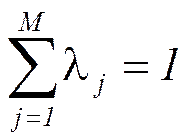
Для критерия Вальда "веса" всех исходов кроме самого плохого - нулевые, зато для наихудшего исхода этот коэффициент равен единице.
Для "максимакса" - наоборот, коэффициент единица присваивается наибольшему исходу, а для остальных они равны 0.
Критерий Лапласа устанавливает всем исходам одинаковые удельные веса, равные 1/М.
В обычном критерии Гурвица ненулевыми являются только коэффициенты для крайних значений, причем они задаются произвольно (при условии, что их сумма равна единице) исходя из степени неприятия ЛПР неопределенности.
При расчете обобщенного критерия Гурвица каждому исходу присваивается свой удельный вес. Формальный способ расчета обеспечивает и соблюдение необходимых условий, и учет отношения к риску.
Подход, основанный на присвоении исходам удельных весов - это один из способов заполнить пробел знаний относительно вероятностного распределения состояний. Один из самых распространенных (но, к сожалению, не всегда самый лучший) критерий сравнения альтернатив в условиях риска - ожидаемое значение - рассчитывается практически также:
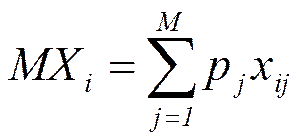 ,
,
Здесь в качестве удельных весов исходов используются их вероятности pj, которые обладают теми же свойствами, что и использованные нами ранее весовые коэффициенты:
0 ≤ pj ≤ 1,
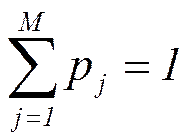
Чем выше вероятность получить конкретный исход - тем больше его удельный вес в этой оценке. В условиях риска вероятности известны, поэтому и используются в расчетах. В ситуации неопределенности мы о них ничего не знаем. Как следствие, мы вынуждены "додумывать" и произвольно присваивать веса, опираясь не на вероятности, а на свое отношение к неопределенности. Знание вероятностного распределения устранило необходимость делать такие допущения и позволило бы принимать более взвешенные решения.
Поэтому в условиях неопределенности теоретически наилучшим подходом является более глубокое исследование ситуации и определение вероятностей. Однако на практике это не всегда возможно или требует серьезных временных и иных затрат. В таком случае остается принимать решения на основе имеющихся данных лишь об исходах, применяя рассмотренные в настоящей главе принципы доминирования и критерии выбора.
Подводя итог рассмотрению критериев выбора, можно сформулировать несколько простых рекомендаций относительно их использования для принятия решений в условиях неопределенности.
1. Нет универсальных критериев. Каждый критерий фокусируется на некоторых свойствах результатов и "затуманивает" другие. Поэтому желательно сравнивать альтернативы не по одному, а по нескольким критериям.
2. Порядок расчета критерия объективен и не зависит от ЛПР. Однако сам выбор критерия для сравнения альтернатив - субъективен и отражает отношение ЛПР к риску. Как следствие, решение, принятое одним ЛПР, не всегда является оптимальным для другого ЛПР. Каждый человек должен сам выбрать именно те критерии, которые наиболее точно соответствуют его отношению к неопределенности.
3. Процедура применения критериев формализована, а сами критерии сильно "упрощают" представление об альтернативах. Из-за этого результаты применения критерия могут быть не совсем логичны с позиций реального человека. Поэтому любое решение, "рекомендуемое" тем или иным критерием, необходимо проверять с позиций "здравого смысла".
В рассмотренном в данной главе примере две альтернативы оценивались последовательно по всем шести критериям. В результате были получены противоречивые результаты. Часть критериев "рекомендовала" первую стратегию, часть - вторую. Каким критериям доверять больше, а каким меньше, должен выбрать ЛПР.
Дата добавления: 2016-03-04; просмотров: 2127;
