Константы и переменные встроенных типов
Константу нельзя изменить в процессе исполнения программы, она может быть записана явно как 3.14 или иметь имя, например Pi. Переменная – это именованный объект, значение которого можно изменить.
Имеется пять встроенных типов:
- числовые:целые integer,вещественные real, комплексные complex;
- логические logical;
- строковые (символьные) character.
Таблица 16. Примеры оформления констант разных типов
| Тип | Примеры явных констант | Разновидности и диапазоны порядков | Пояснения |
| integer | –2147 | integer*1 *2 *4 ±1010 | Точное значение |
| Real | -1.76 1e7 1.2e7 1.3D+123 1.2Q-1234 | real* 4 10±38 7 цифр real* 8 10±308 17 цифр real*1610± 4932 33 цифры | Неточное представление, неточное вычисление |
| Complex | (-1.76 , 1) | Пара вещественных чисел | Неточно |
| Logical | .true. .false. | Logical*1 *2 *4 | 1 бит |
| character | ‘х=’ “O’K” | character*1 до *32767 символов | Кодировка символов ANSI |
Каждому типу соответствует своя область допустимых значений, особый способ хранения в памяти ПК, объём памяти, набор операций ПК.
Атрибут именованной константы parameter, тип и значение входят в ее описание: real,parameter:: Pi =3.141593.
Выражения
Выражение – осмысленная математическая формула, записанная по правилам языка программирования. В отличие от математики формула записывается в виде строк текста; объекты именуются, значки функций заменены именами функций, которые указаны в описании языка и доступны в помощи. В отличие от других языков программирования, выражение может включать не только переменные, но и массивы. В выражение могут входить:
- константа, переменная, элемент массива;
- массив, секция массива;
- вызов функции с аргументами в скобках, например, cos(х-0.2) ;
- операция с одним операндом, например, –х ;
- операция с несколькими операндами, например, x+y+z ;
- парные круглые скобки ( ), квадратных и фигурных скобок нет.
В зависимости от типов объектов, входящих в выражения, различают:
- арифметические (числовые) выраженияс числовым результатом – выполняются операции над числамицелого, вещественного и комплексного типа, выражения могут быть смешанными;
- логические выражения с логическим результатом: логические операции выполняются над логическими величинами, операции отношения – над числами или строками;
- строковые выражения со строковым результатом – выполняются строковые функции и операция сцепления строк, обозначаемая s//p
Арифметическое выражение
Операнды арифметического (числового) выражения могут быть целого, вещественного или комплексного типа.
Таблица 17. В числовом выражении допускаются операции
| Операция | Порядок | Пример | Примечания |
| Вычисление функции | sin(X) | одноместная (унарная) операция | |
| Возведение в степень | X**2 | несколько подряд – справа налево | |
| Смена знака | –X | одноместная (унарная) операция | |
| Деление, умножение | X/Y, X*Y | несколько подряд – слева направо | |
| Сложение, вычитание | X+Y, X-Y | несколько подряд – слева направо |
Знаки двуместных операций - возведение в степень, умножение, деление, сложение и вычитание записываются между операндами. В отличие от математики, знак операции умножения опускать нельзя. Численное значение результата зависит от порядка выполнения операций. Если надо, порядок действий изменяют скобки; разрешаются только круглые. В выражении без скобок операции выполняются в порядке старшинства.
В компьютере имеются два комплекта арифметических операций – для целых и для вещественных чисел. Действия над комплексными числами выполняются программно по правилам, известным из математики с помощью команд для вещественных чисел. Фортран автоматизирует выбор комплекта операций, руководствуясь типом операндов. Если операнды однотипны, то этого же типа будет операция и результат. Для операций с операндами разных типов результат всегда в наиболее широком классе из числа операндов. Множества чисел расширяются так:
– целые – *1 *2 *4 байта;
– шире – вещественные - *4 *8 *16 байтов;
– шире – комплексные - дважды по *4 *8 *16 байтов.
Обратите внимание, что выбор из двух разных операций деления производится по общему правилу:
- при делении вещественных чисел в результате – вещественное число, например, 2./3.=0.666667;
- при делении целых чисел в результате – целое число, равное целой части частного, например, 8/3=2 или 2/3=0;
- при делении разнотипных операндов в результате – вещественное число, например, 2./3=>2./3.=0.6666667 или 2/3.=>2./3.=0.666667 .
Операция возведения в степень an и ax вычисляется программно:
- приinteger nоперацияa**nвыполняетсякак n-кратное умножение a*a*a* ..*a, поэтому a**n=0 при n<0 и integer a, например, 3**(-2)=1/3**2=1/9=0;
- при real x операция a**x выполняется как 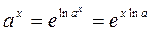 , следовательно, должно быть a > 0 ;
, следовательно, должно быть a > 0 ;
- в общем случае для комплексных a,b 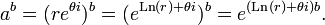 Здесь a=r+θi представлено в экспоненциальной форме, Ln – комплексный логарифм.
Здесь a=r+θi представлено в экспоненциальной форме, Ln – комплексный логарифм.
Все переменные, используемые в выражении, должны быть определены к моменту его вычисления.
При вычислении по формулам следует анализировать ОДЗ, чтобы избегать числовых операций с неопределенным результатом:
- деление на нуль x/0;
- деление нуля на нуль 0/0, 0.0/0.0, 0/0.0, 0.0/0;
- возведение нулевого основания в нулевую или отрицательную степень 0**0 0**(-2);
- недопустимо возведение отрицательного основания в вещественную степень, как в (-8)**(1./3), но -(8**(1./3)) для нечетного 3.
Строковое выражение
Операнды строкового выражения должны быть строкового типа. В строковом выражении допускается только одна операция – сцепление строк (конкатенация). Сцепление обозначается «//», например s=s1//s2, символы в строке s нумеруются слева направо как 1,2,…len(s),
len (s1//s2)=len(s1)+len(s2). Подстрока - несколько символов строки подряд. Пример: результат вычисления ab = ab(14:26)//ab(1:13) – строка, в которой меняются местами первая и вторая половины алфавита:
Character*26 :: ab=’abcdefghijklmnopqrstuvwxyz’
Строка после: ab=’nopqrstuvwxyzabcdefghijklm’
Обратите внимание на то, что оператор s1=s1//s2 с повторением s1 слева и справа от “=” имеет смысл только с подстроками. Нужно, чтобы суммарная длина не превышала len(s1). В Фортране строки имеют постоянную длину, а именно ту, что заявлена в её описании.В то же время оператор s1=trim(s1)//s2 вполне осмысленный, если в s1 хвостовых пробелов, не менее чем символов в s2. Функция trim (s1) обрезает хвостовые пробелы.
Логическое выражение
Логическое выражение имеет значение «истина» или «ложь», состоя из:
- логических констант и переменных;
- пяти логических операций с операндами логического типа;
- шести отношений, которые сравнивают либо два числовых выражения, либо два символьных выражения.
Результат вычисления отношения – либо .true. – «истина», либо .false.– «ложь».
Таблица 18. В Фортране шесть операций отношения
| Отношения | Фортран 90, сейчас пишут так | В стиле Фортран 77, устаревающее |
| меньше чем A<b | a<b | a .lt. b |
| меньше или равно A≤b | a<=b | a .le. b |
| равно A=b | k==m | a .eq. b |
| не равно A≠b | k/=m | a .ne. b |
| больше или равно A≥b | a>=b | a .ge. b |
| больше чем a>b | a>b | a .gt. b |
Отношения вычисляются после вычисления их операндов. Например, при A=2, B=0 для отношения A+3 >B порядок действий такой: сначала вычисляется А+3 и получается 5; затем 5 сравнивается с В, которое равно0; результат вычисления выражения 5>0 – «истина».
Логические операции выполняются после вычисления отношений
Таблица 19.
В Фортране пять логических операций
| Операция | Обозначение | Старшинство | Пример |
| Отрицание НЕ | .not. | .not.a | |
| Конъюнкция И | .and. | a.and.b | |
| Дизъюнкция ИЛИ | .or. | a.or.b | |
| Эквивалентность | .eqv. | a.eqv.b | |
| Неэквивалентность | .neqv. | a.neqv.b |
Операция .not.a является, как и (–x), одноместной (унарной) и пишется перед операндом, остальные знаки логических операций записываются между операндами. Две логические операции могут следовать в выражении непосредственно друг за другом, только если второй операцией является операция отрицания. Например, допустимо a.and. .not.b.
Операция .not. – одноместная и дает результат «истина», если значение операнда «ложь», и результат «ложь», если значение операнда «истина».
Введем обозначения: T – «истина» и F – «ложь».
Таблица 20.
Таблицы истинности пяти логических операций выглядят как
| .AND. | F | T | .OR. | F | T | |
| F | F | F | F | F | T | |
| T | F | T | T | T | T |
| .EQV. | F | T | .NEQV. | F | T | ||||
| F | T | F | F | F | T | ||||
| T | F | T | T | T | F | ||||
| .NOT. | F | T | |||||||
| T | F | ||||||||
Строки и столбцы таблиц истинности помечены значениям операндов, а на пересечении строки и столбца записан результат двухместной операции
Пример логического выражения: a>3 .and.a<5. Выражение истинно, когда оба отношения истинны, то есть аÎ(3,5).
Сложные выражения вычисляются в следующем порядке: числовые операции или строковые операции; операции отношения; логические операции.
Дата добавления: 2016-02-13; просмотров: 857;
