Примеры задач контрольного задания. 1. В функции: вычислить среднее геометрическое положительных элементов одномерного массива

1. В функции: вычислить среднее геометрическое положительных элементов одномерного массива. Если в массиве нет положительных элементов, результат приравнять нулю. В главной программе применить функцию к трем массивам разной длины. Вывести результаты с именами массивов. Найти и вывести минимум среди полученных значений, не равных нулю.

Блок-схема функции обязательна.

2. В подпрограмме: вычислить сумму элементов, расположенных ниже, выше и на главной диагонали квадратной вещественной матрицы. В главной программе: применить подпрограмму к матрице размером 8´8. Вывести три значащих цифры результатов.

Блок-схема подпрограммы обязательна.

3. В вещественном массиве обнулить элементы, синус которых превышает 0.5 (оператор where). Как получить тот же результат без использования оператора where?

4. Исправьте ошибку

Integer i

Real, dimension(7,4):: А

write(*,10) ’Массив’,(A(i,:), i=1,4)

10 Format(a/(4F10.2))

Таблица 14.

Варианты индивидуального задания «Процедуры»

Вариант 1 В подпрограмме 1: транспонировать матрицу. Логический выходной параметр равен .true., если транспонирование выполнимо (иначе .false.) В подпрограмме 2: перемножить две матрицы. Логический выходной параметр равен .true., если умножение матриц выполнимо (иначе .false.)

В главной программе: используяподпрограммы, на примере двух матриц A и B показать, что (AB)T = ATBT. Размеры матриц (не квадратных) выберите сами. Работу подпрограммы 1 проверить, вызвав функцию Transpose, подпрограммы 2 – функциюMatmul. После обращения к каждой подпрограмме выводить сформированную матрицу или аварийное сообщение о невозможности получения результата. После аварийного сообщения завершить программу.

Вариант 2 В функции: вычислить произведение ненулевых элементов одномерного массива, расположенных между максимальным и минимальным элементами. Если между максимумом и минимумом нет ненулевых элементов, результат приравнять нулю. Для проверки вывести координаты максимума и минимума в массиве.

В главной программе: применить функцию к трем массивам разной длины, вывести результаты с именами массивов. Найти и вывести максимум среди полученных значений.

Вариант 3 В подпрограмме: координаты седловых элементов матрицы записать в двумерный массив размером 2´N, в котором каждому элементу соответствует столбец, а N – количество седловых элементов. Седловым считать элемент матрицы, значение которого строго меньше его «соседей» по горизонтали и строго больше «соседей» по вертикали. Учесть, что количество «соседей» элемента колеблется от 2 до 4 в зависимости от его положения в матрице.

В главной программе: воспользоваться подпрограммой для двух матриц, для каждой вывести таблицу с координатами седловых элементов и их значениями.

Вариант 4 В функции: методом трапеций найти по таблице значений f(x)

В главной программе: составить две таблицы значений в интервале [a, b] = [–1, 1.4] с шагом n1 = 0,2 и n2 = 0,04. Применив функцию, вычислить величину интеграла. Сравнить полученные значения с интегралом, вычисленным по первообразной функции. В правильности вычислений убедиться средствами пакета Agrapher.

Вариант 5 В подпрограмме: создать матрицу, в которой каждый отрицательный элемент исходной матрицы заменен средним арифметическим его «соседей» по горизонтали и по вертикали при условии, что все «соседи» неотрицательны. Учесть, что количество «соседей» элемента колеблется от 2 до 4 в зависимости от его положения в матрице. Как выходной аргумент создать двумерный массив, в который записать координаты замененных элементов матрицы.

В главной программе: воспользоваться подпрограммой для двух матриц разных размеров, для каждой вывести измененную матрицу и координаты замененных элементов.

Вариант 6 В функции: реализовать циклический сдвиг матрицы на n элементов вправо, влево, вверх или вниз в зависимости от заданного режима. Значение n может превышать протяженность матрицы по любому измерению.

В главной программе: ввести матрицу и многократно сдвигать ее, меняя направление и величину сдвига в диалоге и используя функцию. После каждого обращения к подпрограмме выводить направление, величину сдвига и полученную в результате матрицу. Работу программы прекратить после ввода слова, отличного от слов Up, Down, Left, Right (например, Stop).

Вариант 7 В подпрограмме: по значениям трех коэффициентов квадратного уравнения найти его корни (действительные или комплексные). Логический выходной параметр равен .true., если корни действительные (иначе .false.).

В главной программе: используя подпрограмму, найти корни 10 уравнений, коэффициенты которых расположены в двумерном массиве размером 3´10 (каждому уравнению соответствует столбец массива). Результаты оформить в виде таблицы.

Вариант 8 В функции: вычислить определенный интеграл как площадь под кривой по формуле трапеций 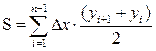, где n – количество значений функции Y в одномерном массиве, а Dx – постоянный шаг изменения аргумента.

В главной программе: сформировать массивы значений функции y = exp(–x/5) в интервале [-2, 2]: a) с шагом Δx1 = 0.1 b) с шагом Δx2 = 0.01. Вычислить определенный интеграл для каждого из этих массивов, сравнить вычисленные значения с определенным интегралом, вычисленным по первообразной функции.

Вариант 9 В подпрограмме: умножить матрицу на вектор. Логический выходной параметр равен .true., если умножение матрицы на вектор выполнимо (иначе .false.)

В главной программе: на примере двух матриц A и B и вектора V показать, что (A+B)V = AV+ BV. Размеры матриц и вектора выберите сами. Работу подпрограммы проверить, вызвав функцию Matmul. После каждого обращения к подпрограмме выводить сформированный вектор или аварийное сообщение о невозможности получения результата. После аварийного сообщения завершить программу.

Вариант 10 В функции: с точностью ε вычислить приближенное значение функции ex при заданных значениях x и ε. Вычисления проводить суммированием членов ряда Тейлора.

В главной программе: значение ε ввести в диалоге и вывести в результирующий файл. Используя функцию, составить и вывести таблицу значений ex, изменяя значение аргумента от xnдо xk с шагом Δx (10 значений). Для проверки дополнить таблицу значениями ex, вычисленными по стандартной программе.

Вариант 11 В подпрограмме: вычислить математическое ожидание и дисперсию случайной величины, значения которой находятся в одномерном массиве. Примечание: дляравномерно распределенной случайной величины математическое ожидание и дисперсия вычисляются по формулам

В главной программе: с помощью генератора псевдослучайных чисел RANDOM_NUMBER создать два одинаковых по длине одномерных массива X и Y, значения которых находятся в интервале [0; 10]. Используяподпрограмму, на примере этих массивов показать, что D(X+Y) = D(X) +D(Y). После каждого обращения к подпрограмме выводить результаты с пояснениями.

Вариант 12 В функции: с точностью ε вычислить приближенное значение функции cos x при заданных значениях x и ε. Вычисления проводить суммированием членов ряда Тейлора (использовать рекуррентную формулу).

В главной программе: Значение ε ввести в диалоге и вывести в результирующий файл. С помощью функции составить вывести таблицу значений cos x, изменяя значение аргумента от xnдо xk с шагом Δx (10 значений). Для проверки дополнить таблицу значениями cos x, вычисленными по стандартной программе.

Вариант 13 В подпрограмме 1: вычислить скалярное (внутреннее) произведение двух векторов.Логический выходной параметр равен .true., если умножение выполнимо (иначе . false.) В подпрограмме 2: вычислить матрицу – внешнее произведение двух векторов. Логический выходной параметр равен.true., если умножение выполнимо (иначе . false.)

В главной программе: применить подпрограммы к двум векторам. Для проверки подпрограммы 1 вызвать функцию Dot_product, подпрограммы 2 – функциюMatmul. После обращения к каждой подпрограмме выводить результат умножения или аварийное сообщение о невозможности его получения. После аварийного сообщения завершить программу.

Вариант 14 В функции: методом прямоугольников вычислить по таблице значений f(x).

В главной программе: составить две таблицы значений 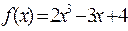в интервале [a, b] = [–1.5, 1.5] с шагом n1 = 0,2 и n2 = 0,04. Применив функцию, вычислить величину интеграла. Сравнить полученные значения с интегралом, вычисленным по первообразной функции. В правильности вычислений убедиться средствами пакета Agrapher.

Вариант 15 В подпрограмме 1: сортировать одномерный массив по убыванию методом последовательного нахождения минимального элемента массива и перестановки его в начало массива. В подпрограмме 2: сортировать одномерный массив по убыванию методом «пузырька». В каждой подпрограмме: подсчитать количество перестановок элементов при сортировке.

В главной программе: с помощью генератора псевдослучайных чисел RANDOM_NUMBER создать одномерный массив, значения которого находятся в интервале [0,10]. Обратившись к подпрограммам, сортировать этот массив по убыванию. Вывести массив до и после сортировки. Сравнить полученные массивы и количества перестановок.

Вариант 16 В функции 1: любым способом сортировать одномерный массив по убыванию. В функции 2: объединить два отсортированных по убыванию массива, не нарушив сортировки.

В главной программе: с помощью генератора псевдослучайных чисел RANDOM_NUMBER создать два одномерных массива разной длины, значения которых находятся в интервале [0; 100]. Обратившись к функции 1, отсортировать эти массивы по убыванию. Вывести массивы до и после сортировки. Используя функцию 2, объединить эти массивы. Вывести объединенный массив.

Вариант 17 В подпрограмме: перемножить две матрицы. Логический выходной параметр равен .true., если умножение матриц выполнимо (иначе . false.).

В главной программе: на примере трех матриц A, B и C показать, что (A+B)C= AC+ BC. Размеры матриц (не квадратных) выберите сами. Работу подпрограммы проверить, вызвав функцию Matmul. После обращения к каждой подпрограмме выводить сформированную матрицу или аварийное сообщение о невозможности получения результата. После аварийного сообщения завершить программу.

Вариант 18 В функции: методом парабол (Симпсона) вычислить по таблице значений f(x).

В главной программе: составить две таблицы значений в интервале [a, b] = [1.5, 2.5] с шагом n1 = 0,1 и n2 = 0,02. Применив функцию, вычислить величину интеграла. Сравнить полученные значения с интегралом, вычисленным по первообразной функции. В правильности вычислений убедиться средствами пакета Agrapher.

Вариант 19 В подпрограмме: вычислить длины сторон, периметр и площадь многоугольника по координатам его вершин. Координаты вершин многоугольника расположены в двумерном массиве, в котором каждой вершине соответствует столбец (первая строка содержит координату x, вторая – координату y).

В главной программе: последовательно читая из файла координаты вершин треугольника, четырехугольника, пятиугольникаи применяя к ним подпрограмму, составить таблицу (длины сторон, периметр и площадь). В отчете привести графическую интерпретацию.

Вариант 20 В функции: получить логическое значение (.true. или .false.), определяющее, расположен ли максимальный отрицательный элемент одномерного массива ранее минимального положительного элемента. Для проверки вывести координаты найденных элементов массива.

В главной программе: применить функцию к трем массивам разной длины. В соответствии с результатами вывести сообщения, указав имена массивов.

Вариант 21 В подпрограмме: методом касательных (Ньютона) вычислить действительный корень уравнения y = (x – 0.5)2 + 1.3e–0.15x + 1.1e–1.5x в интервале [a, b] с абсолютной погрешностью ε. Логический выходной параметр равен .true., если корень существует (иначе . false.).

В пакете Agrapher построить график функции и определить интервалы нахождения корней. В главной программе: дважды применить подпрограмму к каждому из найденных интервалов, приняв абсолютную погрешность равной 10-3 и 10-5. Проверить решение, подставив корни в уравнение. В отчете представить график функции.

Вариант 22 В функции: сформировать матрицу B(m,n) в соответствии с исходной матрицей A(m,n) по правилу .

В главной программе: прочесть из файла две матрицы разных размеров и применить к ним функцию. Вывести исходные и результирующие матрицы.

Вариант 23 В подпрограмме: на интервале [a, b] разбить кривую линию, заданную уравнением, на n участков и вычислить ее длину на этом интервале.

В главной программе: используя подпрограмму, вычислить длину линии, заданной уравнением на интервале [–1, 5] при n1 = 20 и при n2 = 40. Сравнить результаты. В правильности вычислений убедиться средствами пакета Agrapher, вычислив длину линии на заданном интервале по формуле .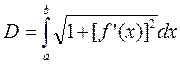

Вариант 24 В функции: вычислить сумму элементов диагонали, параллельной главной диагонали матрицы. Диагональ задаётся координатами ее верхнего элемента.

В главной программе: применить функцию ко всем диагоналям, параллельным главной диагонали матрицы A(6,6), начиная с левого нижнего угла. Составить и вывести одномерный массив из полученных значений.

Вариант 25 В подпрограмме 1: определить количество и составить массив простых чисел в интервале [1; N], используя определение простых чисел. В подпрограмме 2: определить количество и составить массив простых чисел в интервале [1; N], используя алгоритм «Решето Эратосфена».

В главной программе: последовательно применив обе подпрограммы, найти простые числа среди первых 200 чисел натурального ряда. Сравнить результаты применения подпрограмм.

Вариант 26 В функции: подсчитать количество отрицательных элементов внутри прямоугольного фрагмента матрицы M, диагонально противоположными вершинами которого являются элементы с индексами (i1,j1) и (i2,j2).

В главной программе: В каждой из четырех матриц разных размеров найти максимальный и минимальный элементы и применить функцию к прямоугольнику, вершинами которого они являются. Вывести таблицу с координатами найденных вершин и количеством отрицательных элементов в прямоугольнике для каждой матрицы. В исходных данных предусмотреть различное взаимное расположение максимума и минимума для этих матриц.

Вариант 27 В подпрограмме: методом половинного деления вычислить действительный корень уравнения y = (x – 0.6)3 – (x + 4)2 + x + 26.8 в интервале [a, b] с абсолютной погрешностью ε. Логический выходной параметр равен .true., если корень существует (иначе . false.).

В пакете Agrapher построить график функции и определить интервалы нахождения корней. В главной программе: дважды применить подпрограмму к каждому из найденных интервалов, приняв абсолютную погрешность равной 10-3 и 10-5. Проверить решение, подставив корни в уравнение. В отчете представить график функции.

Вариант 28 В функции: вычислить произведение трех наименьших по модулю ненулевых элементов целочисленной матрицы. Если в матрице меньше трех ненулевых элементов, результат приравнять нулю.

В главной программе: применить функцию к трем целочисленным матрицам, разным по размеру. Вывести соответствующие сообщения с именами массивов.

Вариант 29 В подпрограмме: Найти координаты точек, в которых прямая, заданная уравнением kx+b, пересекает стороны треугольника; координаты вершин треугольника расположены в двумерном массиве размером 2´3 (каждой вершине соответствует столбец массива, первая строка содержит координату x, вторая – координату y). Логический выходной параметр равен .true., если прямая пересекает треугольник (иначе .false.)

В главной программе: ввести коэффициенты уравнений пяти прямых и координаты вершин треугольника. Применив подпрограмму к каждой из прямых, составить таблицу (коэффициенты уравнений, координаты точек пересечения прямых со сторонами треугольника). В отчете привести графическую интерпретацию.

Вариант 30 В функции: составить двумерный массив локальных минимумов матрицы (каждой вершине соответствует столбец массива, первая строка содержит координату x, вторая – координату y).. Локальным минимумом считать элемент матрицы, значение которого строго меньше его «соседей» по горизонтали и по вертикали. Учесть, что количество «соседей» элемента колеблется от 2 до 4 в зависимости от его положения в матрице.

В главной программе: применить функцию к трем матрицам разных размеров. Вывести полученные массивы.