Дискриминация для двух групп наблюдений в одномерном случае
7.2 Пусть мы имеем две генеральные совокупности индивидов w1 и w2, из которых получены выборки достаточно большого объема. Пусть по этим выборкам вычислены средние арифметические величины признака X, равные M1 и M2 и дисперсии s12 и s22. Пусть нам известно, что средние величины неравны - M1 ¹ M2. Пусть признак распределен нормально, и пусть распределения признака в совокупностях w1 и w2 размещены на его оси так, как это показано на рисунке 7.1. Рассмотрим возможности отнесения неко-торого наблюдения к одной из двух совокупностей по одному признаку.
Как это известно из свойств нормального распределения, область значений признака, включающая практически все возможные принадлежащие ему наблюдения, ограничена значениями Mi + tsi, где t = 3. Если различия средних арифметических величин настолько велики, что выполняется неравенство
M1 - M2 > ts1 + ts2 (7.1)
при t = 3, то области значений признака в двух распределениях практически не будут пере-секаться. В этом случае нетрудно получить правило, в соответствии с которым можно будет осуществлять дискриминацию, для чего достаточно выбрать некоторое значение признака Xo, которое можно назвать критическим значением дискриминации. Простей-ший способ его получения основан на применении формулы
- 166 -
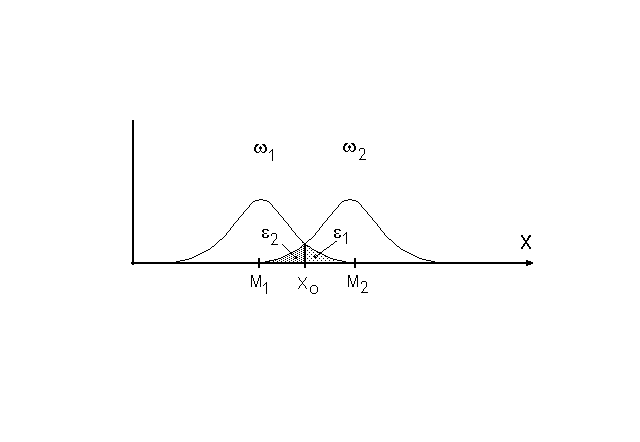
Рисунок 7.1 Определение критического значения дискриминации Xo и ошибок дискриминации e1 и e2
M1 + M2
 Xo = . (7.2)
Xo = . (7.2)
Тогда можно построить так называемое решающее дискриминантное правило, которое будет иметь вид:
если X < Xo, то X принадлежит к w1 (7.3)
если X .³ Xo, то X принадлежит к w2 .
Однако, условие (1) выполняется весьма редко, и обычно для двух распределений признака имеет место перекрывание их размахов вариации. Поэтому, можно видеть (рис.7.1), что использование построенного решающего правила (7.3) всегда будет сопро-вождаться ошибками (табл.7.1). Так, мы можем отнести индивида, оказывающегося на рисунке 7.1 немного правее критического значения, к совокупности w2, тогда как он возможно размещается в зоне правого "хвоста" распределения w1 . Аналогичная ошибка может быть совершена и при отнесении наблюдения из w2 к совокупности w1 , если оно оказывается правее уровня Xo и располагается в зоне правого «хвоста» соответствующего распределения признака для w1. Эти возможные ошибки дискриминации и соответствую-щие им вероятности (e1 и e2) перечислены в таблице 7.1
- 167 -
Таблица 7.1. Ошибки дискриминации в случае двух совокупностей
| Объективная ситуация | Субъективное решение | |
| Наблюдение отнесено к w1 | Наблюдение отнесено к w2 | |
| Наблюдение относится к w1 | Верное решение | Ошибка с вероятностью e1 |
| Наблюдение относится к w2 | Ошибка с вероятностью e2 | Верное решение |
Как это видно на рисунке 7.1, вероятность e1 равна площади под кривой распределе-ния признака X в совокупности w1, ограниченной слева перпендикуляром, восставлен-ным из критического значения Xo. Аналогичная вероятность e2 равна площади кривой распределения X в w2, ограниченной справа тем же перпендикуляром. Согласно свой-ствам нормального распределения эти вероятности можно получить из формул

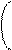 Xo - M1
Xo - M1
 e1 = 1 - F(t1) = 1 - F ,
e1 = 1 - F(t1) = 1 - F ,
s1 (7.4)
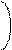
 M2 - Xo
M2 - Xo
 e2 = F(t2) = F ,
e2 = F(t2) = F ,
s2
где F(ti) - интегральная функция нормального распределения. Учитывая, что таблицы этой функции составлены для положительных значений нормированных отклонений при ti > 0, обе формулы можно переписать как
ei = 1 - F ½ ti ½ . (7.5)
7.3 Одним из путей определения критического значения дискриминации Xo является нахождение его по формуле (7.2) Xo = (M1 + M2)/2. Этот способ обеспечивает равенство двух вероятностей совершить ошибки e1 = e2 в ситуации, когда распределения признака X нормальны и средние квадратические отклонения равны s1 = s2. В ситуации, когда последнее условие не выполняется, равенство ошибок дискриминации обеспечит получение критического значения дискриминации по формуле
s1M2 + s2M1
 Xo = . (7.6)
Xo = . (7.6)
s1 + s2
Решающее правило (7.3) не учитывает возможных различий в неодинаковой частоте встречаемости индивидов из совокупностей w2 к w1 . Эти частоты могут быть выражены через так называемые априорные вероятности P1 и P2 (P1 + P2 = 1). Если индивиды из обе-их совокупностей могут встретиться одинаково часто, то P1 = P2 = 1/2. Если это - не так, то в решающем правиле следует учитывать различия P1 и P2. Одной из форм такого учета является так называемое отношение правдоподобия
- 168 -
f1(X)
 l(X) = , (7.7)
l(X) = , (7.7)
f2(X)
где f1(X) и f2(X) - значения дифференциальной функции распределения в 1-й и 2-й сово-купности для величины признака X. Критическое значение этого отношения равно
P1
 l(Xo) = - (7.8)
l(Xo) = - (7.8)
P2
отношению априорных вероятностей. Если l(Xi) > l(Xo), то наблюдение Xi относится к w1, если l(Xi) < l(Xo), то Xi относится к w2 . Тогда можно выписать решающее правило диск-риминации в следующем виде:
f1(Xi) P1

 Если l(Xi) = ³ , то Xi принадлежит к w1 ,
Если l(Xi) = ³ , то Xi принадлежит к w1 ,
f2(Xi) P2 (7.9)
f1(Xi) P1

 Если l(Xi) = < , то Xi принадлежит к w2 .
Если l(Xi) = < , то Xi принадлежит к w2 .
f2(Xi) P2
Иногда применяется величина -ln [l(Xi)]. Тогда это решающее правило можно переписать в виде
Если -ln [l(Xi )] > ln (P1/P2) то Xi принадлежит к w1 ,
Если -ln [l(Xi )] < ln (P1/P2) то Xi принадлежит к w2 . (7.10)
Формулы (7.9) и (7.10) описывают так называемый байесовский критерий, минимизи-рующий ошибку дискриминации. Критическое значение Xо можно найти как такую вели-чину признака, где дифференциальные функции двух распределений f1(Xi ) и f2(Xi ) соот-носятся так, что выполняется условие
f1(Xi) P1

 l(Xi) = = = l(Xo) . (7.11)
l(Xi) = = = l(Xo) . (7.11)
f2(Xi) P2
Если априорные вероятности равны P1 = P2 = 1/2, то выражение (7.11) превращается в f1(Xi) = f2(Xi) и значение Xo в случае равных дисперсий признака s1 = s2 определяется по формуле (7.2). В антропологических исследованиях чаще считается, что априорные вероятности равны.
Дата добавления: 2016-02-13; просмотров: 743;
