Достаточные признаки сходимости знакопостоянных рядов.

Пусть даны два знакоположительных ряда 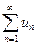(1) и 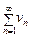(2). Если для всех 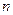выполняется неравенство 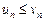, то из сходимости ряда (2) следует сходимость ряда (1), а из расходимости ряда (1) следует расходимость ряда (2).

В качестве рядов для сравнения удобно рассматривать:

–геометрическую прогрессию 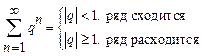– гармонический ряд 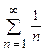, который расходится;

– ряд Дирихле ,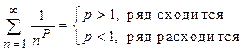

Пример 6. Исследовать на сходимость ряд .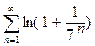

Решение

Так как данный n-й член ряда имеет вид ln(1+ 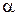), где 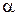- бесконечно малая величина при n 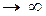, и известно, что ln(1 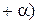~ 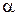, то этот ряд сравниваем с рядом

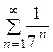, представляющим собой бесконечно убывающую геометрическую прогрессию со знаменателем q=1/7<1, которая сходится, следовательно, и исходный ряд сходится. ●

Пример 7. Исследовать ряд .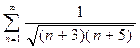

Решение

n-й член данного ряда: 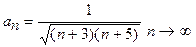~ 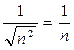, т.е. при n 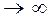ведет себя как гармонический, следовательно, ряд также расходится. ●

Часто, прежде чем использовать какой-либо из достаточных признаков сходимости ряда, необходимо использовать понятие эквивалентных бесконечно малых величин при 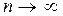и обязательно проверить необходимые условия сходимости исследуемого ряда.