Лекция 6. Статистическое изучение динамики.
Социально-экономические явления общественной жизни находятся в непрерывном развитии, т.е. в динамике. Их изменения во времени в статистике изучается при помощи построения и анализа рядов динамики (их также называют динамическими, временными или хронологическими рядами).
6.1.Виды рядов динамики. Средний уровень ряда динамики.
Ряд динамики – это последовательность упорядоченных во времени значений статистических показателей, характеризующих уровень развития исследуемого явления. Элементами динамического ряда являются два ряда чисел: время 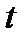 и конкретное значение показателя или уровень ряда
и конкретное значение показателя или уровень ряда 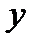 . Уровни выражаются в виде абсолютных, относительных и средних величин статистических показателей. Различают моментныеи интервальные ряды динамики. У моментных рядов уровни характеризуют объёмы явления в определенные моменты времени (например, показатели численности населения на начало года, величины запаса какого-либо материала на начало периода), а у интервальныхрядов уровни характеризуют объёмы явления за какие-то периоды (например, ряды показателей объёма продукции по месяцам года, количества отработанных человекодней по отдельным периодам). Если уровни интервального ряда представляют собой абсолютные величины, то их уровни можно суммировать или дробить во времени, получая новые численные значения объёма явления. Уровни же моментных динамических рядов суммировать нельзя; сумма не имеет смысла, так как каждый последующий уровень полностью или частично включает в себя предыдущий уровень. Однако разность уровней имеет смысл, характеризуя увеличение или уменьшение уровня ряда между датами учета.
. Уровни выражаются в виде абсолютных, относительных и средних величин статистических показателей. Различают моментныеи интервальные ряды динамики. У моментных рядов уровни характеризуют объёмы явления в определенные моменты времени (например, показатели численности населения на начало года, величины запаса какого-либо материала на начало периода), а у интервальныхрядов уровни характеризуют объёмы явления за какие-то периоды (например, ряды показателей объёма продукции по месяцам года, количества отработанных человекодней по отдельным периодам). Если уровни интервального ряда представляют собой абсолютные величины, то их уровни можно суммировать или дробить во времени, получая новые численные значения объёма явления. Уровни же моментных динамических рядов суммировать нельзя; сумма не имеет смысла, так как каждый последующий уровень полностью или частично включает в себя предыдущий уровень. Однако разность уровней имеет смысл, характеризуя увеличение или уменьшение уровня ряда между датами учета.
Важнейшим условием правильного формирования рядов динамики является сопоставимость уровней, образующих ряд, т.е. осуществление смыкания рядов динамики.
| Пример 6.1.Объём инвестиций по фирме характеризуется следующими данными:
Приведенный ряд дает неправильное представление о динамике инвестиций, так как показатели относятся к периодам с различной продолжительностью. Чтобы выявить изменение объёма, следует определить величину капитальных вложений на одну и ту же единицу каждого периода. Объём капитальных вложений за один год составляет: | ||||||||||||||||||||||||||||||||||
Пример 6.2. Общий объём продукции в одном из регионов (в млн. руб.):
Здесь показатели за 1991 –1993 гг. не сопоставимы непосредственно с показателями 1995 – 1997 гг., так как относятся к различным границам региона. Для приведения ряда динамики к сопоставимому виду для 1994 г. определим коэффициент соотношения уровней двух рядов:
|
Методы расчета среднего уровняряда зависят от его вида и способов получения статистических данных. В интервальном ряду с равноотстоящими уровнями расчет среднего уровня ряда 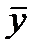 производится по формуле простой средней арифметической:
производится по формуле простой средней арифметической:
 (6.1)
(6.1)
где 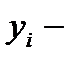 уровни ряда;
уровни ряда; 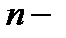 число уровней ряда.
число уровней ряда.
Если интервальный ряд имеет не равноотстоящие уровни, то средний уровень вычисляется по формуле взвешенной средней:
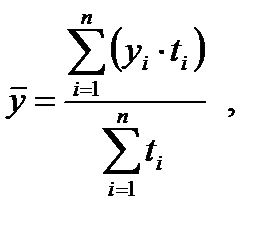 (6.2)
(6.2)
где 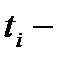 длительность периода времени, в течение которого ряд имел уровень
длительность периода времени, в течение которого ряд имел уровень  .
.
Для моментного ряда с равноотстоящими уровнями средний уровень ряда рассчитывается с помощью средней хронологической:
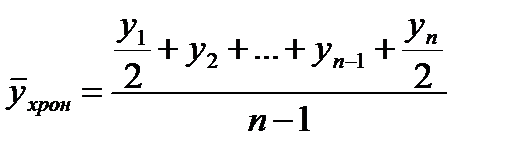 , (6.3)
, (6.3)
где 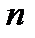 – число уровней ряда.
– число уровней ряда.
Пример 6.3. Рассмотрим моментный динамический ряд: товарные запасы в торговом предприятии на начало каждого месяцахарактеризуются следующими данными:
Средние товарные запасы за 1-й квартал, можно найти, используя формулу средней хронологической (6.3):
От моментного ряда можно перейти к интервальному ряду. Для этого определим средние запасы за месяц: за январь:
Средние запасы за 1-й квартал рассчитываем, используя формулу простой средней арифметической (6.1):
|
Для моментного ряда с неравными интервалами 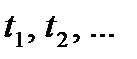 предварительно находятся значения уровней в серединах интервалов:
предварительно находятся значения уровней в серединах интервалов: 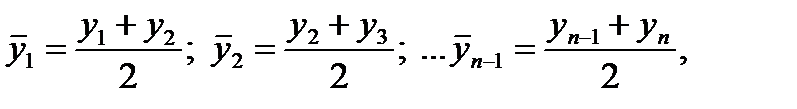 а затем определяется средний уровень ряда:
а затем определяется средний уровень ряда:
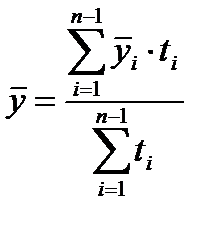 . (6.4)
. (6.4)
| Пример 6.4. Товарные запасы на начало каждого месяцахарактеризуются следующими данными:
Определяем средние запасы за интервал:
|
Дата добавления: 2016-02-27; просмотров: 1024;

 1987–1992 гг. –
1987–1992 гг. –  ; 1993–1996 гг. –
; 1993–1996 гг. – 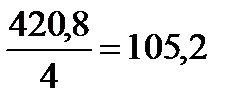 ; 1997–1999 гг. –
; 1997–1999 гг. – 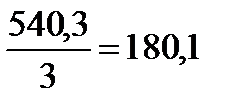 ; 2000 г. – 200,5. Как видно из этих данных, объём капитальных вложений снижался до 1997 г., и лишь начиная с 1997 г. наметилось некоторое его повышение.
; 2000 г. – 200,5. Как видно из этих данных, объём капитальных вложений снижался до 1997 г., и лишь начиная с 1997 г. наметилось некоторое его повышение.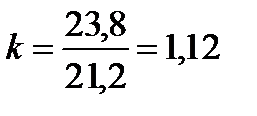 . Умножив на этот коэффициент уровни первого ряда, получают скорректированные данные за 1991 – 1993 гг. в новых границах. Таким образом, сопоставимый ряд динамики имеет вид:
. Умножив на этот коэффициент уровни первого ряда, получают скорректированные данные за 1991 – 1993 гг. в новых границах. Таким образом, сопоставимый ряд динамики имеет вид: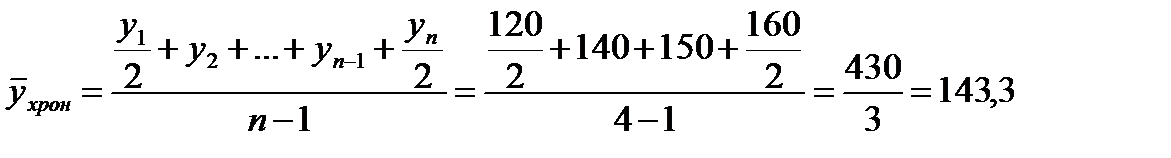 млн. руб.
млн. руб.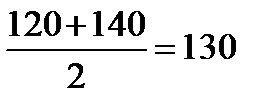 млн. руб.; за февраль:
млн. руб.; за февраль: 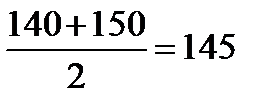 млн. руб.; за март:
млн. руб.; за март:  млн. руб.
млн. руб.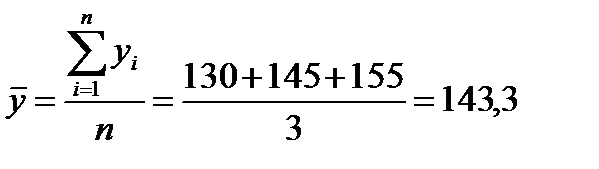 млн. руб.
млн. руб.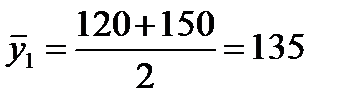 млн. руб.;
млн. руб.; 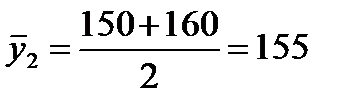 млн. руб. Вычислим средние товарные запасы за 1-й квартал (11.4):
млн. руб. Вычислим средние товарные запасы за 1-й квартал (11.4):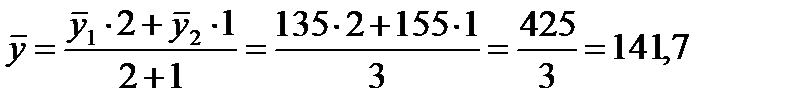 млн. руб.
млн. руб.