Искусственное начальное решение
пример. min z = 4x1 + x2.

max (– z) = – 4x1 – x2.

Если начальное решение x1 = x2 = 0, то
 – не является допустимым решением.
– не является допустимым решением.
Добавляем искусственные переменные Ri.

Начальное решение x1 = x2 = 0.
 – не является допустимым решением.
– не является допустимым решением.
Исходная задача будет иметь решение только в том случае, когда полученная задача имеет решение R1 = R2 = 0.
Двухэтапный метод
1) min r = R1 + R2.
Если эта задача имеет решение при r = 0 при R1 = R2 = 0, то исходная задача также имеет решение, причем оптимальное решение составленной задачи является начальным решением исходной.
Если же r = R1 = R2 = 0 не выполняется, то исходная задача решений не имеет.
2) Решается исходная задача
min r = R1 + R2; max (– r) = – R1 – R2.
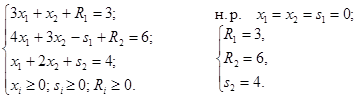
| Б | С | Xопт | – 1 | – 1 | r | ||||
| x1 | x2 | s1 | s2 | R1 | R2 | ||||
| R1 | – 1 | 3/3 | |||||||
| R2 | – 1 | – 1 | 3/2 | ||||||
| s2 | |||||||||
| – r | – 9 | – 7 | – 4 | ||||||
| x1 | 1/3 | 1/3 | |||||||
| R2 | – 1 | 5/3 | – 1 | – 4/3 | 3/4 | ||||
| s2 | 5/3 | – 1/3 | 9/5 | ||||||
| – r | – 2 | – 5/3 | 7/3 | ||||||
| Б | С | Xопт | – 4 | – 1 | – 1 | – 1 | |||
| x1 | x2 | s1 | s2 | R1 | R2 | ||||
| x1 | 0 (– 4) | 3/5 | 1/5 | 3/5 | – 1/5 | r = 0 R1 = 0 R2 = 0 | |||
| x2 | 0 (– 1) | 6/5 | – 3/5 | – 4/5 | 3/5 | ||||
| s2 | 0 (0) | – 1 | |||||||
| – r | |||||||||
| – z | – 18/5 | – 1/5 | |||||||
| x1 | – 4 | 2/5 | – 1/5 | ||||||
| x2 | – 1 | 9/5 | 3/5 | ||||||
| s2 | |||||||||
| – z | – 17/5 | 1/5 |
Итак, 
Метод больших штрафов (М – метод)

max (– z) = – 3x1 – 2x2 – 3x3 – MR1 – MR2.
M>>1.
R1 = R2 = 0 – Если это получим, то исходная задача имеет решение, если этого не получим, то исходная задача не имеет решения.
| Б | С | Xопт | – 3 | – 2 | – 3 | – M | – M | ||
| x1 | x2 | x3 | s1 | s2 | R1 | R2 | |||
| R1 | – M | – 1 | |||||||
| R2 | – M | – 1 | |||||||
| – z | –10M | 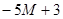
| 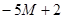
| 
| M | M | |||
| R1 | – M | 5/4 | 1/2 | – 1 | 1/4 | не надо | |||
| x2 | – 2 | 3/4 | 1/2 | – 1/4 | не надо | ||||
| – z | –4 | 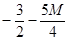
| 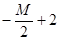
| M | 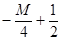
| не надо | |||
| x1 | – 3 | 2/5 | – 4/5 | 1/5 | не надо | не надо | |||
| x2 | – 2 | 1/5 | 3/5 | – 2/5 | не надо | не надо | |||
| – z | –4 | 7/5 | 6/5 | 1/5 | не надо | не надо |
x1 = 0; x2 = 0; x3 = 0; max (– z) = – 4; min z = 4.
Дата добавления: 2016-02-27; просмотров: 534;
