Стандартная форма записи задачи линейного программирования
Общий вид задачи линейного программирования.
Найти значения переменных x1, x2, x3, ... , xn, при которых максимума или минимума max (min) достигает целевая функция.
z = c1x1 + c2x2 + ... + cnxn
Если для переменных x1, x2, ... , xn выполняются ограничения
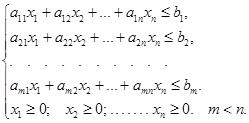
Точки для которых выполняются ограничения называются допустимыми решениями (или планами). Множество точек допустимых решений образуют многоугольник допустимых решений.
Матричная форма записи задачи линейного программирования получится, если мы введем такие матрицы:

пример.
Процесс изготовления двух видов промышленных изделий заключается в последовательной обработке каждого из них на трех станках. Время использования каждого из этих станков ограничено 10 часами в сутки. Время обработки и прибыли от продаж каждого изделия приведены в таблице.
| Время обработки, мин | ||||
| изделие | 1 станок | 2 станок | 3 станок | прибыль |
Нужно определить оптимальные объемы производства изделия каждого вида.
Решение
Пусть изделий 1го вида изготавливается x1 штук, а 2го вида – x2 штук.
Прибыль: max z = 2x1 + 3x2.
Ограничения: 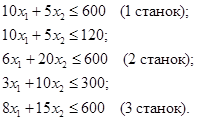
Итак, max z = 2x1 + 3x2;

Графический метод задачи линейного программирования с двумя переменными
max (min) z = c1x1 + c2x2;

Чтобы решить графически нужно выполнить следующее:
1) построить многоугольник допустимых решений
2) если при некоторых значениях x1, x2 целевая функция z = a, то прямая c1x1 + c2x2 = a будет перпендикулярна нормаль вектору 
3) если решается задача на максимум, то a должно увеличиваться, поэтому двигая прямую перпендикулярно  в направлении
в направлении  до тех пор пока прямая не будет иметь только одной общей точки с многоугольником допустимых решений. В этом положении прямая называется опорной, а координата полученной точки опорным решением (или планом). При решении задачи на минимум прямую двигаем против направления
до тех пор пока прямая не будет иметь только одной общей точки с многоугольником допустимых решений. В этом положении прямая называется опорной, а координата полученной точки опорным решением (или планом). При решении задачи на минимум прямую двигаем против направления  .
.
Продолжаем рассматривать начатый выше пример.
max z = 2x1 + 3x2;

Решение
(1) 
пробная точка O (0, 0):  выполняется.
выполняется.
O (0, 0) лежит в полуплоскости
 (2)
(2) 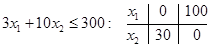
O (0, 0):  выполняется.
выполняется.
(3) 
O (0, 0):  выполняется.
выполняется.
z = 2x1 + 3x2;
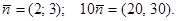
Двигаем  до точки А.
до точки А.
А – опорное решение
Найдем координаты точки А.
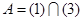
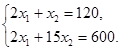

Прибыль: 
Симплекс-метод
Очевидно, что оптимальное решение достигается в вершине многоугольника допустимых решений. При решении задачи линейного программирования симплекс-методом осуществляется последовательный переход от некоторой произвольно выбранной начальной вершины (обычно начало координат) к смежным вершинам до той поры, пока не будет найдено оптимальное решение. Симплекс-метод применяется только в стандартной форме записи задачи линейного программирования.
Стандартная форма записи задачи линейного программирования

1) Если в ограничении есть знак ≤, то мы прибавляем к левой части остаточную переменную
x1 – 2x2 ≤ 5; x1 – 2x2 + s1 = 5; s1 – остаточная переменная s1 ≥ 0;
2x1 + 3x2 ≥ 10; 2x1 + 3x2 – s2 = 10; s2 – избыточная переменная s2 ≥ 0.
2) max z = (– a) Û min (– z) = a.
Решение, полученное занулением n – m переменных называется базисным. Переменные не равные нулю называются базисными переменными, а равные нулю – небазисными.
шаг 0 начальное решение (xi = 0).

| базис | С | Xопт | r | |||||
| x1 | x2 | s1 | s2 | s3 | ||||
| s1 | ||||||||
| s2 | 30 | |||||||
| s3 | ||||||||
| z | – 2 | – 3 |
z – строка оценок;
“С” ´ столб – (оценка в верхней строчке);
Xопт = 0·120 + 0·300 + 0·600 – 0 = 0;
x1: 0·2 + 0·3 + 0·8 – 2 = – 2 и т.д.
шаг 1
Если в строке нет отрицательных, то оптимальное решение получено. Столбец, в котором стоит наибольшая по модулю отрицательная оценка является разрешающим. Переменная этого столбца вводится в базис. x2 – разрешающая; x2 вводится в базис.
шаг 2
Находим отношение элементов столбца Xопт к положительным элементам разрешающего столбца. Строка, в которой отношение наименьшее является разрешающей, соответствующая переменная выводится из базиса.

s2 выводится из базиса, разрешающая.
На пересечении разрешающей строки и разрешающего столбца стоит главный элемент.
шаг 3
Пересчитываем коэффициенты таблицы с помощью преобразований Гаусса.
| базис | С | Xопт | r | |||||
| x1 | x2 | s1 | s2 | s3 | ||||
| s1 | 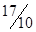
| 
| 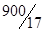
| |||||
| x2 | 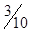
| 
| ||||||
| s3 | 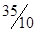
| 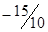
| 
| |||||
| z | 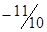
| 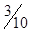
| ||||||
| s1 | 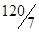
| |||||||
| x2 | 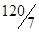
| |||||||
| x1 | 
| |||||||
| z | 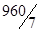
| 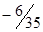
| 
| |||||
| s2 | 
| |||||||
| x2 | 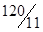
| |||||||
| x1 | 
| |||||||
| z | 
| 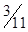
| 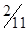
|
Особые случаи применения симплекс-метода
1. Вырождение решение
 Одна из базисных переменных на некотором этапе равна 0. Графически это означает избыточное ограничение.
Одна из базисных переменных на некотором этапе равна 0. Графически это означает избыточное ограничение.
пример. max z = 3x1 + 9x2.


| Б | С | Xопт | r | ||||
| x1 | x2 | s1 | s2 | ||||
| s1 | 2; 
| ||||||
| s2 | 2; 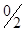
| ||||||
| z | – 3 | – 9 | |||||
| s1 | – 1 | – 2 | |||||
| x2 | 
| 
| |||||
| z | 
| 
|
x2 = 2; s1 = 0; x1 = s2 = 0; z = 18.
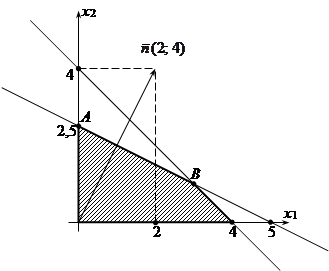 2. Альтернативное решение
2. Альтернативное решение
пример. max z = 2x1 + 4x2.
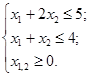

АВ – множество решений

| Б | С | Xопт | r | ||||
| x1 | x2 | s1 | s2 | ||||
| s1 | 
| ||||||
| s2 | |||||||
| z | – 2 | – 4 | |||||
| x2 | 
| 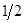
| 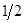
| ||||
| s2 | 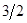
| 
| 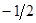
| ||||
| z | |||||||
| x2 | – 1 | ||||||
| x1 | – 1 | ||||||
| z |

 Используем формулу: x = a·α + b·(1 – α); α Î [0; 1]
Используем формулу: x = a·α + b·(1 – α); α Î [0; 1]


3. Неограниченное решение
пример. max z = 2x1 + x2.

max z = ∞
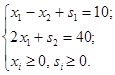
| Б | С | Xопт | r | ||||
| x1 | x2 | s1 | s2 | ||||
| s1 | – 1 | ||||||
| s2 | |||||||
| z | – 2 | – 1 |
Столбец x2 не содержит положительных, значит сразу можно сделать вывод о неограниченности максимума.
max z = ∞
Дата добавления: 2016-02-27; просмотров: 2786;
