Равенство множеств. Подмножество. Универсальное множество. Дополнение множества

Множество, элемент множества, пустое множество

В обычной речи мы часто употребляем слово "множество": множество людей, множество книг, множество законов, множество денег и т.д.

Под множеством будем понимать совокупность, набор каких- либо предметов (объектов). Предметы, составляющие множество, называются его элементами. То, что элемент а входит в множество А, записывается так: аÎА (читается, а есть элемент множества А, или: а принадлежит множеству А). Запись аÏА означает, что элемент а не принадлежит множеству А, Термин "множество" употребля­ется независимо от того, много или мало в этом множестве элементов. Мно­жество, не содержащее ни одного элемента, называется пустым и обозначается символом Æ.

Примерами пустых множеств могут служить:

а) множество действительных чисел, являющихся корнями уравнения х² + 1 = 0;

6) множество треугольников, сумма углов которых отлична от 180°,

Множество можно задать:

ü перечислив все его элементы. Например, множество учеников в классе задается перечислением фамилий в классном журнале. Это нетрудно сделать, так как такое множество содержит конечное число элементов. Однако не - всякое конечное множество можно задать перечислением. Множества слонов на нашей планете или рыб в океане тоже конечные, но попробуйте их перечислить (или пересчитать!).

ü если указать некоторое свойство, которым обладают все его элементы и не обладают никакие другие объекты. Такое свойство называется характеристическим свойством множества. Одно и то же множество может быть задано различными характеристическими свойствами. Например, множество {2,4} может быть задано как:

а) множество четных чисел, удовлетворяющих неравенству 1<х<5;

б) множество корней квадратного уравнения х²-6х+8=0.

Записывается это таким образом: А={х:1<x<5 и х - четное} или А={х: х²-6х+8=0}.

В геометрии множество точек, обладающих данным характеристическим свойствам, часто называют геометрическим местом точек с данным свойством. Биссектриса угла есть геометрическое место точек плоскости, лежащих внутри этого угла и равноудаленных от его сторон. Окружность - геометрическое место точек плоскости, расстояние которых от данной точки О (центра окружности) равно числу R (радиусу окружности).

Равенство множеств. Подмножество. Универсальное множество. Дополнение множества

Если А и В два множества, то запись А=В означает, что они состоят из одних и тех же элементов. Если каждый элемент множества А является в то же время элементом множества В, то говорят, что А - подмножество в В, и пишут АсВ. Каждое непустое множество имеет, по крайней мере, два подмножества: пустое множество Æ и само множество А.

Приведем примеры подмножеств:

а) множество жителей г. Мирный является подмножеством множества жителей России;

б) множество всех квадратов есть подмножество множества всех прямоугольников;

в) множество Z всех целых чисел есть подмножество множества Q всех рациональных чисел.

Если одновременно с отношением АсВ имеет место отношение ВсА, то А=В. То есть, если одновременно А есть подмножество В и В есть подмножество А, то такие два множества равны.

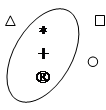Введенные в этом параграфе отношения наглядно иллюстрируются с помощью так называемых диаграмм Венна. Диаграмма Венна - это замкнутая линия, внутри которой расположены элементы данного множества, а снаружи - элементы, не принадлежащие этому множеству. Например, диаграмма множества В={*,+,®}

Отношение АсВ с помощью диаграмм можно изобразить

Пусть нам дано какое-либо множество E. Мы будем рассматривать всевозможные подмножества данного множества Е. Исходное множество Е в таком случае называют универсальным множеством. В качестве примера возьмем множество книг. В это множество входят подмножества научных, художественных книг, книг по искусству; среди научных книг есть подмножества книг по математике, химии, биологии и т.д. Множество всех книг - это универсальное множество, содержащее в себе различные подмножества книг. Сколько этих подмножеств? - Очень много! - скажете Вы. - Тогда давайте рассмотрим пример попроще.

Пусть универсальное множество Е состоит из трех элементов {a,b,c}. Перечислим все подмножества Е: {а}, {Ь}, {с}, {a,b}, {a,с}, {b,c}, {a,b,c}, {Æ}. Их всего 2³=8 подмножеств. Можно доказать, что если универсальное множество Е состоит из n элементов, т.е. число всех подмножеств множества Е равно 2ⁿ.

Пусть множество А есть некоторое подмножество универсального множества Е. Тогда множество А, состоящее из всех элементов множеств Е, не принадлежащих множеству А, называется дополнением множества А. Например, если А - множество всех девушек в группе, то дополнением А является множество всех юношей. Дополнением множества всех квадратов в множестве всех прямоугольников является множество всех прямоугольников с неравными сторонами. Если Е={целые числа}, А={четные числа}, то 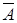={нечетные числа}.

3. Операции над множествами: объединение, пересечение, разность.

A. Объединением С двух множествА и В называется множество, состоящее из всех элементов, принадлежащих множеству А или множеству В. Обозначают это так: С=АÈВ.Элементы зачисляются в объединение С только один раз. Иными словами, в объединение входят все элементы, принадлежащие хотя бы одному из множеств. Объединение часто называется суммой множеств.

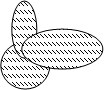
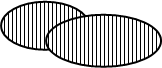
Примеры:

а) Обозначим через А множество точек круга R₁, а через В -множество точек круга R₂. Тогда их объединением будет множество точек фигуры, ограниченной на рисунке жирной линией.

б) Обозначим через А множество успевающих учеников в группе, через В множество девушек в этой группе и через С множество неуспевающих мальчиков. Тогда AÈBÈC является множеством всех учащихся этой группы. Множества А и В имеют общие элементы - успевающих девушек.

в) Обозначим через А множество целых чисел, через В множество четных чисел. Тогда AÈBесть множество А, то есть АÈВ=А.

B. Пересечением С двух множеств А и В называется множество, состоящее из элементов, принадлежащих множеству А и множеству В одновременно. Обозначают это так: C=AÇB.

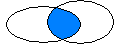
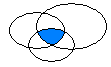
Примеры:

а) Термин "пересечение" по существу геометрического происхождения. Пересечением прямой и плоскости, если прямая не параллельна плоскости, является их единственная общая точка. Если прямая и плоскость параллельны, то пересечение этих множеств пусто. Если же прямая лежит на плоскости, то их пересечение совпадает с множеством точек этой прямой.

б) ПустьА - множество мальчиков, обучающихся в техникуме, в В - множество всех студентов из группы ПВ02. Тогда пересечение AÇB - множество мальчиков, которые учатся в этой группе.

в) Пусть А - множество натуральных делителей числа 72: А={1,2,3,4,6,8,9, 12,18,24,36,72}, а В - множество натуральных делителей числа 54-В={1,2,3,6,9,18,27,54}. Тогда множество AÇB={ 1,2,3,6,9,18}, Эти числа являются общими делителями для 72 и 54. Наибольший элемент множества AÇB, то есть 18, называется наибольшим общим делителем чисел 54 и 72.

Множество делителей числа 72 и 54 конечно. А множество кратных этого числа бесконечно: С={72,144,216,,,.,72n,..} и D= {54,108,162,216,,..,54m,..,}.

Пересечением этих множеств является множество общих кратных для чисел 72 и 54; CÇD={216,432,..}.

Наименьшее число в СÇD, то есть 216, называется наименьшим общим кратным для 72 и 54.

C. Разностью С двух множеств А и В называется множество, состоящее из всех элементов А, не входящих в В. Обозначают это так: C=А\B. Для разных случаев заштрихованные множества - это разность А\В двух множеств.

Примеры.

а) Если А - множество всех студентов техникума, а В - множество всех- девочек, которые учатся в техникуме, то А\В - множество всех мальчиков, которые обучаются в техникуме.

б) Пусть А - множество натуральных четных чисел, а В - множество всех целых чисел, делящихся на 4. Тогда А\В - множество всех четных натуральных чисел, которые не делятся на 4.

в) Разностью множества четных чисел и множества целых чисел является пустое множество.

Иными словами, пересечение образовано всеми общими элементами данных множеств. Аналогично определяется пересечение, объединение и разность трех и более множеств.