Несвободное истечение
Несвободное истечение наблюдается, если глубина воды в нижнем бьефе русла влияет на расход жидкости, вытекающей из-под щита (рис. 9.23).
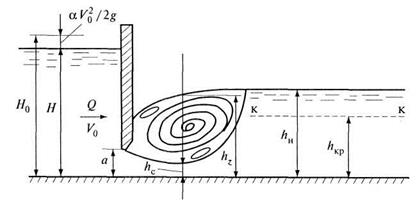
Рис. 9.23. Несвободное истечение из-под щита
В нижнем бьефе поток находится в спокойном состоянии (hн > hкр ), и сопряжение бьефов происходит в виде затопленного прыжка (h"c < hн).
При несвободном истечении расход будет зависеть от перепада уровней жидкости перед затвором и за ним непосредственно в сжатом сечении:
Q=μab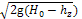 
, (9.57)
где μ — коэффициент расхода; hz — глубина над сжатым сечением.
При сопряжении в виде затопленного прыжка коэффициент расхода
μ= εφ (значения φ и ε соответствуют свободному истечению).
Лабораторные исследования многих авторов показали, что в случае несвободного истечения потока из-под щита коэффициент расхода имеет те же значения, что и при свободном истечении. Исследованиями было установлено, что глубина непосредственно за щитом несколько меньше глубины потока в нижнем бьефе.
Глубина hz может быть определена при заданном расходе по уравнению
hz=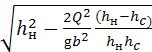 
. (9.58)
Глубина сжатого сечения находится так же, как и для свободного истечения, hc = εа.
Для приближенного расчета расхода можно принять hz = hн, тогда
Q= μab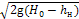 
. (9.59)
В этом случае коэффициент расхода определяется по следующей формуле:
μ=0,6+ 
. (9.60)
Граничные условия применения формулы (9.59):
0,1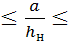 
0,75 .
Пример 9.5
Определить расход потока воды Q, вытекающего из-под плоского вертикального щита, если перед ним глубина Н= 2,0 м, открытие а = 0,70 м, ширина отверстия b = 3,0 м, глубина в нижнем бьефе hн = 1 м (см. рис. 9.22).
Находим n=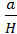 
= 
= 0,35.
Определим коэффициент сжатия струи по формуле (9.56):
ε=0,57+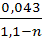 
=0,57+ 
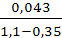=0,627 .
Глубина потока воды в сжатом сечении
hc = εa= 0,627 • 0,7 = 0,439 м.
Полагаем, что имеет место свободное истечение из-под щита.
При свободном истечении расход определяем по формуле (9.55), считая φ= 1,0:
Qп=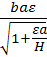 
= 
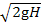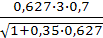
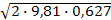=7,45 м/c.
Находим скорость подхода к щиту:
V0=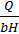 
= 
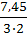=1,21 м/с.
Вычисляем число Фруда:
Fr=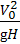 
= 
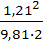= 0,075 .
Коэффициент скорости по табл. 9.5 φ = 0,96.
Расход воды равен Q = φQп = 0,96 • 7,45 = 7,15 м3/с
Уточняем форму сопряжения бьефов при истечении из-под щита.
Критическая глубина в прямоугольном русле
hкр=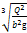 
= 
= 0,83 м.
Вычисляем сопряженную с hс фиктивную глубину h c ":
h c "=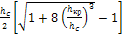 
= 
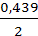
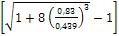= 1,41 м.
Так как h"с > hн , форма сопряжения будет в виде отогнанного прыжка, следовательно, истечение свободное (hн = 1 м).
Пример 9.6
Определить расход воды Q, вытекающей из-под плоского вертикального щита, установленного в канале прямоугольной формы шириной b = 3 м. Глубина воды перед щитом Н =3 м, высота поднятия щита а=0,3 м, глубина воды в нижнем бьефе канала hн=1,8 м (см. рис. 9.23).
Предположим, что истечение воды из-под щита несвободное. Расход вычисляем по формуле (9.59):
Q= μab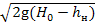 
..
Граничные условия применения данной формулы выражаются отношением
, 
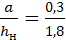
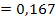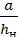>0,1.
Коэффициент расхода (9.60)
μ=0,6+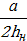 
= 0,6+ 
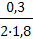= 0,683.
Примем H0=H,
Q=0,683·0,3·3 
=2,98 м3/с
Средняя скорость потока перед щитом
V0= =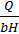 
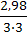= 0,33 м/c
Скоростной напор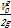 
= 
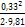= 0,0056 м.
Скоростной напор из-за своей малой величины не влияет на расход при истечении. Определяем форму сопряжения при истечении.
Глубина сжатого сечения hс = εа. Коэффициент сжатия ε находим по формуле (9.56):
n= 
= 
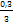= 0,1 м;
ε= 0,57+ 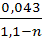=0,57+ 
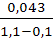=0,613;
hc=0,613·0,3=0,184 м.
Критическая глубина в прямоугольном канале
hкр=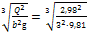 
=0,465 м.
Фиктивная глубина, сопряженная с hс = 0,185 м,
hc''=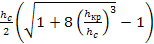 
= 
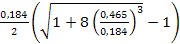=0,957 м.
Глубина в нижнем бьефе hн = 1,8 м; hн > hc".
Следовательно, форма сопряжения - затопленный прыжок, истечение несвободное.
Дата добавления: 2016-02-27; просмотров: 786;