Отверстие затопленное
Рассматриваем малое отверстие в тонкой стенке, из которого происходит истечение под уровень жидкости (рис. 6.2). Давления на свободные поверхности жидкости в резервуарах равны атмосферному 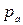 . Поверхности уровней как в правом, так и в левом резервуаре не изменяют своего положения за определенное время.
. Поверхности уровней как в правом, так и в левом резервуаре не изменяют своего положения за определенное время.
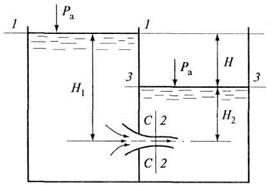
Рис. 6.2. Истечение под уровень жидкости
Напишем уравнение Бернулли для сечений 1-1 и 3-3 относительно плоскости сравнения, проходящей через центр отверстия параллельно свободным поверхностям в резервуарах:
 ;
;
 ;
; 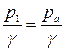 ;
;  ;
;  (6.13)
(6.13)
Пренебрегаем величинами  и
и  вследствие их малости, так как площади поперечных сечений резервуаров
вследствие их малости, так как площади поперечных сечений резервуаров 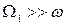 и
и  (
( 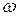 - площадь малого отверстия). После подстановок получим
- площадь малого отверстия). После подстановок получим
 , (6.14)
, (6.14)
где  ;
; 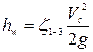 - гидравлические потери напора;
- гидравлические потери напора;  - коэффициент сопротивления, учитывающий потери напора от сечения 1-1 до сечения 3-3;
- коэффициент сопротивления, учитывающий потери напора от сечения 1-1 до сечения 3-3; 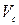 - средняя скорость течения в сжатом сечении С-С (2-2).
- средняя скорость течения в сжатом сечении С-С (2-2).
Потери напора между выбранными сечениями состоят из потерь при истечении из отверстия, т.е. от сечения 1-1 до 2-2 (С-С) и от сечения 2-2 до сечения 3-3, где происходит внезапное расширение струи до существенно больших размеров:
 (6.15)
(6.15)
Потери при истечении из отверстия
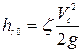 .
.
Потери при внезапном расширении струи определяем по формуле Борда (4.126):
 ,
,
где 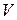 - скорость в резервуаре при расширении струи,
- скорость в резервуаре при расширении струи,  .
.
Потери напора будут
 . (6.16)
. (6.16)
Скорость в сжатом сечении
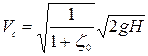 (6.17)
(6.17)
или
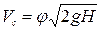 .
.
Формула расхода для сжатого сечения при истечении через затопленное отверстие:
 . (6.18)
. (6.18)
Полученная формула расхода аналогична формуле расхода для незатопленного отверстия. Различие формул заключается в том, что напор истечения Н выражает разность уровней  жидкости в резервуарах.
жидкости в резервуарах.
Установлено при проведении многочисленных опытов, что значения  ,
,  для затопленного и незатопленного отверстий практически одинаковы. Поэтому в случае определения расхода или скорости через затопленное отверстие коэффициенты принимаются такими же, как и для незатопленного отверстия. На основании опытов разных авторов А. Альтшулем был создан график для малых круглых отверстий коэффициентов
для затопленного и незатопленного отверстий практически одинаковы. Поэтому в случае определения расхода или скорости через затопленное отверстие коэффициенты принимаются такими же, как и для незатопленного отверстия. На основании опытов разных авторов А. Альтшулем был создан график для малых круглых отверстий коэффициентов  ,
,  ,
,  в зависимости от числа Рейнольдса (рис. 6.3). Для квадратичной области сопротивления при турбулентном режиме, т.е. при больших числах
в зависимости от числа Рейнольдса (рис. 6.3). Для квадратичной области сопротивления при турбулентном режиме, т.е. при больших числах  , принимаются
, принимаются 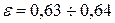 ;
;  ;
; 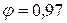 ;
;  .
.

Рис. 6.3. Зависимость коэффициентов истечения из малых отверстий в тонкой стенке от числа Рейнольдса
Пример 6.1
Определить длину трубопровода диаметром  мм, при котором расход вытекающей воды будет такой же, как из малого отверстия того же диаметра, если напоры воды соответственно равны
мм, при котором расход вытекающей воды будет такой же, как из малого отверстия того же диаметра, если напоры воды соответственно равны  м и
м и 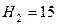 м . Коэффициент гидравлического трения трубы принять равным
м . Коэффициент гидравлического трения трубы принять равным  . Температура воды
. Температура воды  (рис. 6.4).
(рис. 6.4).
Формулы расхода при истечении жидкости из отверстия и трубы:
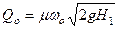 ;
;
 .
.
Площади поперечных сечений отверстия и трубы ( 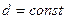 ) равны
) равны  .
.

Рис. 6.4. К примерам 6.1 и 6.8
Расходы  , тогда
, тогда
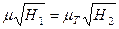 .
.
Коэффициент расхода малого отверстия 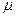 найдем, используя зависимость
найдем, используя зависимость 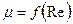 (см. рис. 6.3).
(см. рис. 6.3).
Определим число Рейнольдса
 ,
,
 м/с2 при
м/с2 при  (табл. П1.4 приложения).
(табл. П1.4 приложения).
По графику (см. рис. 6.3) находим для полученного Re  .
.
Коэффициент расхода трубы
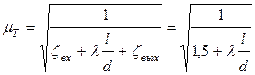 ,
,
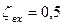 ;
;  (табл. П 1.4 приложения).
(табл. П 1.4 приложения).
Возведем в квадрат равенство расходов, полученное ранее:
 ,
,
Откуда
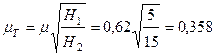 ;
;
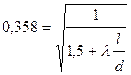 .
.
Из полученного выражения находим длину трубопровода:
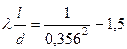 ;
;
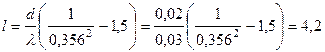 м.
м.
Длина трубопровода 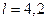 м.
м.
Пример 6.2
Два резервуара, напоры в которых поддерживаются постоянными и равными соответственно 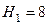 м и
м и  м, соединены между собой короткой трубой длиной
м, соединены между собой короткой трубой длиной 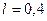 м. Расход воды, протекающий из одного резервуара в другой,
м. Расход воды, протекающий из одного резервуара в другой,  л/с. Температура воды
л/с. Температура воды  . Определить диаметр трубы, приняв
. Определить диаметр трубы, приняв  (рис. 6.5).
(рис. 6.5).

Рис. 6.5. К примеру 6.2
Напор, при котором происходит истечение воды из одного резервуара в другой,
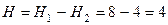 м.
м.
Расход воды определяется по формуле
 .
.
Коэффициент расхода короткой трубы  при
при 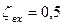 ;
;  (табл. П 1.5 приложения)
(табл. П 1.5 приложения)
 .
.
Диаметр трубы находим методом подбора, задаваясь разными значениями d. Вычисления  и
и  сводим в табл. 6.1.
сводим в табл. 6.1.
Таблица 6.1 - Результаты вычисления
| № п/п | d, м | 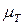
| Q, м3/с |
| 0,03 | 0,739 | 0,0046 | |
| 0,04 | 0,756 | 0,0084 | |
| 0,05 | 0,767 | 0,0133 |
Диаметру d=50 мм соответствует расход Q=13,3 л/с, что удовлетворяет условию примера.
Дата добавления: 2016-02-27; просмотров: 638;
