Примеры решения задач. Пример 3.1.14. Определить параметры состояния (Р, υ, t, u, i, s) в крайних точках цикла газотурбинной установки простейшей схемы
Пример 3.1.14. Определить параметры состояния (Р, υ, t, u, i, s) в крайних точках цикла газотурбинной установки простейшей схемы, работающей при следующих исходных данных (рис. 3.1.3):
начальное давление сжатия Р1 = 0,1 МПа,
конечное давление сжатия Р2 = 0,5 МПа,
начальная температура сжатия t1 = + 15 °С,
начальная температура процесса расширения t3 = 750 °С.
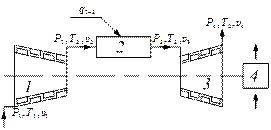
Рис. 3.1.3. Схема простейшей газотурбинной установки
1 – осевой компрессор; 2 – камера сгорания; 3 – турбина; 4 – нагрузка
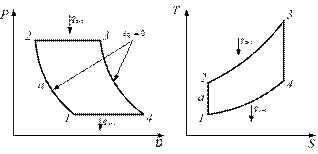
Рис. 3.1.4. Цикл газотурбинной установки в координатах Р-υ и Т-S
Внутреннюю энергию u, энтальпию i определить относительно Т0 = 0 К, а энтропию s определить относительно состояния при Т0 = 273,2 К, Р0=0,101 МПа.
Для каждого процесса цикла определить работу, количество подведенного или отведенного тепла, изменение внутренней энергии, энтальпию и энтропию.
Определить работу цикла, количество подведенного и отведенного тепла, термический КПД цикла, сравнить его с КПД цикла Карно, имеющего одинаковые с расчетным циклом максимальную и минимальную температуры.
Построить цикл в координатах Р-υ и Т-S. Рабочее тело — 1 кг воздуха (R=0,287 кДж/кг∙К, СP=1,006 кДж/кг∙К; СV=СP – R=0,719 кДж/кг∙К).
Для воздуха применимо уравнение состояния идеального газа Pυ = RT.
Решение
1. Определение параметров состояния в крайних точках цикла.
Точка 1.
P1=0,1 МПа; t1=+ 15°С; Т1=t1 + 273,2=288,2 К;
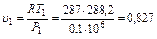 м3/кг;
м3/кг;
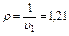 кг/м3;
кг/м3;
i1=СP T1=1,006∙288,2 = 289,9 кДж/кг;
ul = CV T1=0,719∙288,2 = 207,2 кДж/кг;
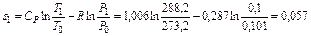 кДж/кг∙К.
кДж/кг∙К.
Следует заметить, что если определение энтропии в точке идет при совпадающем значении давления P1=Р0, то уравнение упрощается и принимает вид 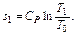
Точка 2.
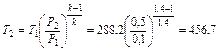 К;
К;
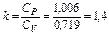 ;
;
t2=T2 - 273,2 = 183,5 °С;
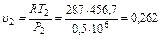 м3/кг;
м3/кг;
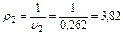 кг/м3;
кг/м3;
i2=CP∙T2=1,006∙456,7=459,4 кДж/кг;
и2=CV∙T2=0,719∙456,7=328,4 кДж/кг;
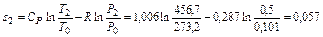 кДж/кг∙К.
кДж/кг∙К.
Точка 3.
Р3=Р2=0,5 МПа; Т3=t3 + 273,2 = 1023,2 °К;
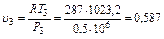 м3/кг;
м3/кг;
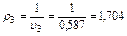 кг/м3;
кг/м3;
i3=CP∙T3=1,006∙1023,2=1029,3 кДж/кг;
и3=CV∙T3=0,719∙1023,2=735,7 кДж/кг;
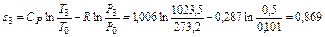 кДж/кг∙К.
кДж/кг∙К.
Точка 4.
Р4=Р1=0,1 МПа;
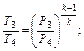
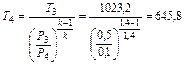 К;
К;
t4=T4 - 273,2 = 376,6 °С;
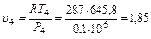 м3/кг;
м3/кг;
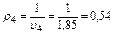 кг/м3;
кг/м3;
i4=CP∙T4=1,006∙645,8=649,7 кДж/кг;
и4=CV∙T4=0,719∙645,8=470,8 кДж/кг;
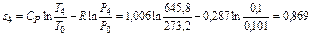 кДж/кг∙К.
кДж/кг∙К.
2. Построение цикла в координатах Р-υ и Т-s.
Процессы, изображаемые в Р-υ и Т-s координатах, необходимо строить не менее чем по трем точкам.
Для нахождения параметров промежуточных точек вначале надо принять произвольно значение одного какого-либо параметра таким образом, чтобы это значение находилось между его численными значениями в крайних точках процесса. Последующий параметр определяется из уравнения, характеризующего данный процесс, составленного для одной (любой) из крайних точек процесса и для промежуточной точки.
Процесс 1-2. Точка «а». Принимаем Ра=0,3 МПа. По уравнению адиабаты идеального газа Pυk =C для точек «а» и 1 имеем Ра∙υkа = Р1∙υk1 или
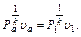
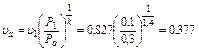 м3/кг;
м3/кг;
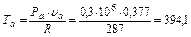 К;
К;
ta=120,9 oC;
ia=CP∙Ta=1,006∙394,1=396,5 кДж/кг;
иa=CV∙Ta=0,719∙394,1=283,4 кДж/кг;
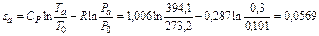 кДж/кг∙К.
кДж/кг∙К.
Аналогично определяются параметры на всех других процессах рассматриваемого цикла. По найденным значениям строится цикл в координатах Р-υ и Т-s. Масштаб выбирается произвольно исходя из численных значений параметров.
3. Определение работы, количества подведенного или отведенного тепла, изменение внутренней энергии, энтальпии и энтропии для каждого процесса цикла.
Процесс 1-2 (адиабатический, δq = 0)
q1,2 = Δu + l1,2 = Δi + w1,2 = 0
Потенциальная работа
w1,2 = i1 – i2 = CP(T1 – T2) = 1,006(288,2 – 456,7) = - 169,5 кДж/кг –
работа затрачивается.
Термодинамическая работа
l1,2 = u1 – u2 = CV(T1 – T2) =0,719(288,2 - 456,7) = - 121,2 кДж/кг;
Δi = i2 – i1 = 169,5 кДж/кг;
Δu = u2 – u1 = 121,2 кДж/кг,
Δs1,2 = 0, так как q1,2 = 0.
Процесс 2-3 (изобарический, Р = idem)
l2,3 = P2(υ3 – υ2) = 0,5∙105(0,587 – 0,262) = 0,162∙105 кДж/кг;
w2,3 = 0;
q2,3 = i3 – i2 = CP(T3 – T2) = 1,006(1023,2 — 456,7) = 569 кДж/кг, -
тепло подводится
Δu2,3 = CV(T3 – T2) = 0,719(1023,2 - 456,7) = 407,3 кДж/кг;
l2,3 = q2,3 + Δu2,3 = 569,7 - 407,3 = 162 кДж/кг,
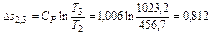 кДж/кг∙К,
кДж/кг∙К,
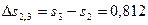 кДж/кг∙К.
кДж/кг∙К.
Процесс 3-4 (адиабатический, δq = 0)
q3,4 = Δu3,4 + l3,4 = Δi3,4 + w3,4 = 0;
w3,4 = i3 – i4 = CP(T3 – T4) = 1,006(1023,2 – 645,8) = 379,7 кДж/кг;
l3,4 = u3 – u4 = CV(T3 – T4) =271,4 кДж/кг;
Δs3,4 = 0, так как q3,4 = 0.
Процесс 4-1 (изобарический, Р = idem)
w4,1 = 0;
q4,1 = Δi4,1 + w4,1 = CP(T1 – T4) ==1,006(288,2 - 645,8)= - 359,7 кДж/кг –
тепло отводится.
Δu4,1 = CV(T1 – T4) = 0,719(288,2 - 645,8) = - 257,1 кДж/кг;
l4,1 = P (υ1 – υ4) = 0,5∙105(0,827 - 1,85) = - 0,102∙105 кДж/кг;
из первого начала термодинамики q4,1 =Δu4,1 + l4,1 имеем:
l4,1 = q4,1 – Δu4,1 = - 359,7 - (-257,1) = - 102,6 кДж/кг – работа подводится
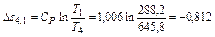 кДж/кг∙К,
кДж/кг∙К,
или
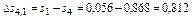 кДж/кг∙К.
кДж/кг∙К.
Данные вычислений сводятся в табл. 3.1.6, 3.1.7.
Таблица 3.1.6
Результаты вычислений по точкам
| Точки | Параметры | ||||||
| Р, МПа | υ, м3/кг | t, °С | Т, К | l, кДж/кг | и, кДж/кг | s, кДж/кг∙К | |
| 0,1 | 0,827 | 288,2 | 289,9 | 207,2 | 0,057 | ||
| 0,5 | 0,262 | 183,5 | 456,7 | 459,4 | 328,4 | 0,057 | |
| 0,5 | 0,587 | 1023,2 | 1029,3 | 735,7 | 0,869 | ||
| 0,1 | 1,85 | 372,6 | 645,8 | 649,7 | 470,8 | 0,869 |
Таблица 3.1.7
Результаты вычислений по процессам
| Процессы | l, кДж/кг | w, кДж/кг | Δi, кДж/кг | Δи, кДж/кг | q, кДж/кг | Δs, кДж/кг∙К |
| 1-2 | -121,2 | -169,5 | 169,5 | 121,2 | ||
| 2-3 | 567,7 | 407,3 | 569,7 | 0,812 | ||
| 3-4 | 274,4 | 379,7 | -379,4 | 271,4 | ||
| 4-1 | -109,6 | -359,7 | -257,1 | -359,7 | -0,812 |
Работа цикла
Термодинамическая работа
lц = l1,2 + l2,3 + l3,4 + l4,1 = - 121,2 + 162 + 271,4 - 102,6 ≈ 210 кДж/кг.
Потенциальная работа
wц = w1,2 + w2,3 + w3,4 + w4,1 = - 169,5 + 379,7 = 210 кДж/кг.
В круговых процессах lц = wц.
Количество полезно использованного тепла в цикле
qпол = q2,3 – q4,1 = 210 кДж/кг.
В круговом термодинамическом процессе количество подведенного тепла численно равно работе:
q = lц = wц = 210 кДж/кг.
Термический КПД цикла
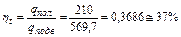 .
.
КПД цикла Карно, имеющего одинаковые с расчетным циклом максимальную и минимальную температуры
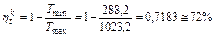 .
.
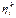 > ηt.
> ηt.
Пример 3.1.15. Провести термодинамический расчет цикла паросиловой установки (цикл Ренкина), работающей при следующих исходных данных.
Начальное давление пара, то есть давление перед турбиной Р1 = 5 МПа = 50 Бар. Начальная температура пара, то есть температура пара перед турбиной t1 = 500 °С; T1 = t1 + 273,2 = 773,2 К. Конечное давление отработанного пара, т.е. давление пара за турбиной, в конденсаторе Р2 = 0,01 МПа = 0,1 бар.
Требуется определить:
1) параметры пара в крайних точках цикла и представить цикл в координатах Р-υ и T-s и i-s;
2) внутренний абсолютный КПД цикла;
3) удельный часовой расход пара;
4) удельный часовой расход тепла;
5) количество охлаждающей воды, необходимой для конденсации пара в течение 1 часа, если вода нагревается при этом на 10°C.
Мощность паросиловой установки принимается равной N = 2500 кВт.
Решение
Паросиловая установка по циклу Ренкина работает следующим образом (рис. 3.1.5). Вода насосом V подается в паровой котел I, при этом давление ее повышается с величины Р2 до Р1. Так как вода практически не сжимается (υ=const), то в координатах Р-υ (рис. 3.1.6) этому процессу соответствует процесс 3-4 (υ=idem), а в координатах Т-s и i-s этот процесс из-за малости масштаба практически выглядит как совмещенная точка 3-4 (Слишком близко друг от друга здесь расположены изобары P1 и Р2).
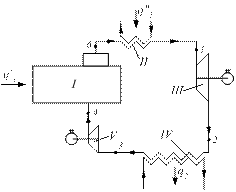
Рис. 3.1.5. Принципиальная схема паросиловой установки
В паровом котле вода подогревается вначале от температуры точки 4 до температуры точки 5, где она достигает величины температуры кипения. Эта температура будет больше или меньше в зависимости от давления P1. Так при давлении P1 = 0,1 МПа температура в точке 5 будет равна ≈ 100°С; а при Р = 0,2 МПа кипение, воды будет начинаться уже при температуре ≈ 120°С и т.д. Таким образом, отрезок изобары 4-5 в координатах Р-υ -соответствует процессу нагревания воды при постоянном давлении до температуры кипения. Температуру кипения, при которой вода превращается в пар, называют температурой насыщения, а пар, образующийся при этом, — влажным насыщенным паром.
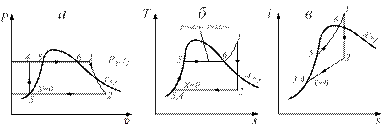
Рис. 3.1.6. Цикл паросиловой установки в координатах Р-υ и T-s и i-s
При дальнейшем подводе тепла в паровом котле 1 количество жидкой фазы постепенно уменьшается, а количество пара увеличивается. Температура смеси остается постоянной (рис. 3.1.6), так как все подводимое тепло идет на испарение жидкой фазы. Этот процесс на рис. 3.1.6 изображается отрезком 5-6, который одновременно является изобарой и изотермой. То есть процесс парообразования 5-6 является изобарно-изотермическим.
В точке 6 последняя капля воды превращается в пар и пар теперь называется сухим насыщенным паром. При дальнейшем подводе тепла в пароперегревателе II (q’’1) при том же давлении P1 происходит увеличение температуры пара, пар перегревается. Точка 1 на рис. 3.1.6 соответствует, состоянию перегретого пара и, в зависимости от температуры T1, может лежать дальше или ближе от точки 6.
Далее пар с параметрами P1, T1, поступает в паровую турбину, где расширяется адиабатически до давления Р2. После расширения пара в паровой турбине и получения полезной работы от турбины отработанный пар поступает в холодильник-конденсатор IV, где за счет внешнего охлаждения полностью конденсируется. Вода вновь поступает на вход насоса V и цикл повторяется.
Для цикла Ренкина характерно, прежде всего, то, что в нем не учитываются какие-либо потери в различных стадиях цикла, присутствует одно и то же количество вещества и, главное, происходит полная конденсация водяных паров в холодильнике-конденсаторе на линии 2-3. При этом отводится тепло в количестве q2.
Дата добавления: 2016-02-27; просмотров: 3479;
