Примеры решения задач. Пример 2.2.7. Вода (t = 20 °С) перетекает из резервуара А в резервуар В, давления на поверхности жидкости
Пример 2.2.7. Вода (t = 20 °С) перетекает из резервуара А в резервуар В, давления на поверхности жидкости, в которых одинаковы, (рис. 2.2.30). Соединительный трубопровод состоит из двух последовательно соединенных участков новых бесшовных труб (l1 = 200 м, d1 = 100 мм и l2 = 50 м, d2=80 мм), для обеих труб l экв = 0,05l, h = 3м.
Определить расход воды.
Решение
Хотя вода - жидкость маловязкая (h = 10-3 Па∙с, см. прил. 4), но квадратичная зона сопротивления сомнительна, так как мала эквивалентная шероховатость труб (∆ = 0,014 мм, см. прил. 1). Поэтому решаем задачу графоаналитическим способом.
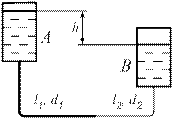
Рис. 2.2.30.
1. Зададимся рядом значений Q и вычислим соответствующие этим значениям hпот для каждого из участков, после чего суммируем их для каждого Q. Полученные результаты приведены ниже, где hобщ = h1+h2.
| Q 103, м3/с … | |||||||
| h1, м………... | 0,18 | 0,36 | 0,60 | 0,89 | 1,23 | 1,62 | 2,06 |
| h2, м……….. | 0,38 | 0,79 | 1,31 | 1,96 | 2,72 | 3,59 | 4,56 |
| hобщ , м……... | 0,56 | 1,15 | 1,91 | 2,58 | 3,95 | 5,21 | 6,63 |
2. По выбранным значениям Q и вычисленным для них hобщ строим гидравлическую характеристику всего трубопровода.
3. Составив уравнение Бернулли для живых сечении, выбранных по уровням жидкости в резервуару получим:
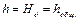
4. Отложив на оси ординат величину Hд = 3 м, находим искомый расход Q = 5,15 дм3/с.
Убедимся, что предположение о квадратичном законе сопротивления было бы ошибочным.
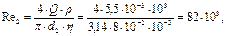
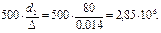
Проверка велась только по d2, так как Re2 > Re1. Ответвления от основной магистрали могут быть замкнутыми (рис. 2.2.31, а) и разомкнутыми (рис. 2.2.31, б). Для замкнутых ответвлений (лупингов - от англ. «петля» - соединенный параллельный трубопровод) справедливы соотношения
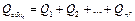 (2.2.18)
(2.2.18) 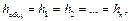 (2.2.19)
(2.2.19)
где Qобщ и hобщ - соответственно расход и потери напора на всей разветвленном участке. Следовательно, расход, проходящий через весь разветвленный участок, равен сумме расходов в отдельных ветвях (для рис. 2.2.30, Qобщ = Q1 + Q2), а потери напора для всего разветвления и в любой его ветви равны между собой.
При аналитическом способе решения задачи на основании анализа исходных данных предсказывается режим движения (для турбулентного движения также зона сопротивления). Затем, используя соотношение (2.2.18) и (2.2.19), определяют скорость (или расход) в каждой из ветвей, после чего находят потери напора в одной из них. Принятое предположение подтверждается проверочными расчетами.
Пример 2.2.8.По трубопроводу (см. рис. 2.2.31, а) перекачивается нефть (ρ = 900кг/м3, ν = 2·10-4 м2/с с расходом Q = 50 дм3/с.
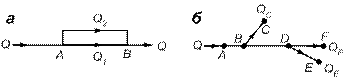
Рис. 2.2.31. Схемы сложных трубопроводов
а – трубопровод с замкнутым ответвлением (лупингом);
б – трубопровод с разомкнутыми ответвлениями
Определить относительное изменение потерь напора на участке А – B=5 км (d1= 200 мм), если к нему подключить лупинг той же длины (d2 = 260 мм). Трубы сварные новые, местными сопротивлениями пренебречь.
Решение
1. Определим потери напора на участке A - B до подключения к нему лупинга.
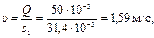
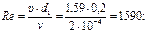
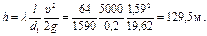
2. Найдем соотношение между Q1 и Q2, после подключения лупинга.
Режим движения в трубах должен остаться ламинарным, так как по формуле (2.2.18) Q1 и Q2, меньше Q.
Используя соотношение (1.2.19), с учетом ламинарного режима имеем:

или, проведя сокращения и заменив υ1 на Q1, а υ2 на Q2 получим (можно было сразу воспользоваться формулой Пуазеля):
 , откуда
, откуда
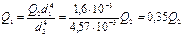
3. Определим Q1 и Q2 и проверим правильность предположения о ламинарном режиме движения.
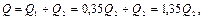 откуда
откуда

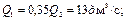

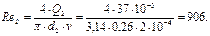
Предположение о ламинарном течении подтвердилось.
4. Определим потери напора во всем разветвлении через потери напора в лупинге. По формуле Пуазеля
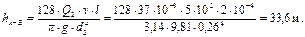
5. Вычислим относительное изменение потерь напора
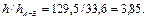
Следовательно, после подключения лупинга потери напора на участке А-В уменьшились почти в 4 раза.
При графоаналитическом способе решения строят гидравлические характеристики для каждой из параллельных ветвей и, исходя из соотношений (2.2.18) и (2.2.19), путем сложения абсцисс для ряда точек этих кривых, получают гидравлическую характеристику всего разветвленного участка. Для схемы трубопровода на рис. 2.2.31 такое построение показано на рис. 2.2.32.
При разомкнутом разветвлении из одного узла (точки соединения разветвляющихся участков трубопровода) решение задачи можно получить, если для каждой из ветвей составить уравнение Бернулли, выбрав сечения в их начале и конце. Например, для ветвей DE и DF (см. рис. 2.2.31, б), сходящихся в угле D, такие уравнения будут иметь вид:
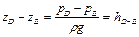 и
и 

|

|
Рис. 2.2.32. Характеристика сложного Рис. 2.2.33.
трубопровода, имеющего замкнутое
ответвление
Так как zD и pD в этих уравнениях общие, то, разрешив уравнения
относительно рD/(pg) и приравняв, можно найти или расходы, идущие в каждую ветвь (QE и QF в данном примере, если известно Q = QE + QF), или, при заданных расходах, требуемые диаметры труб каждой из ветвей.
Пример 2.2.9. По временному трубопроводу (рис. 2.2.33) бензин (Q = 50 дм3/с, ρ = 740 кг/м3, v = 0,55·10-6 м2/с) подается в стоянки для залива цистерн. От основной линии (АВ = l=2 км, dAB = d = 200 мм) в узле В поток разделяется в линии ВС (lВС = l1 = 100 м, dBC = d1 = 125 мм) и BD (lBD = /2 = 150 м, dBD =d2 = 150 мм). Все трубы сварные умеренно заржавленные, превышение точек С и D над горизонтальной осью трубы АВ: zС = 10 м, zD = 13 м.
Определить расходы бензина QC и QD и избыточное давление рА, развиваемое насосом. Местными сопротивлениями и скоростными напорами пренебречь, конечное давление рС и pD атмосферное.
Решение
1. Для определения расходов QC и QD составим уравнения Бернулли для участков между сечениями В - С и В - D
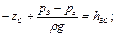
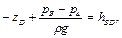 (2.2.20)
(2.2.20)
откуда hBC = hBD + (zD – zC). (2.2.21)
2. Определим расходы QC и QD.Так как жидкость течет маловязкая, а трубы имеют значительную шероховатость, предполагаем в обеих ветвях квадратичную зону сопротивления. В этом случае, выразив hBС и hBD по формуле Дарси-Вейсбаха, а значение λ — по формуле Шифринсона, уравнение (2.2.21) можно записать в виде
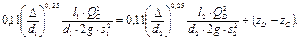 (2.2.22)
(2.2.22)
Подставив численные значения входящих в уравнение (2.2.22) величин, получим 0,761Q2C·104 = 0,4362 Q2D·104 + 3. Отсюда, учитывая, что QC + QD = Q, окончательно имеем:
QC = 26,6 дм3/с, QD = 23,4 дм3/с.
Проверка показывает, что Re1 = 4,96·105 > 500d1/Δ = 1,25·105, a Re2 = 3,64·105 > 500 d2/Δ = 1,5·105 .
Следовательно, предположение о квадратичной зоне сопротивления оправдалось, и расходы QC и QD определены правильно.
3. Определим избыточное давление в точке В, т.е. рВи = рB - pа.
По уравнению (2.2.20) рBи = (hBC + zС)ρg или рВи = (hBD + zD)ρg.
Выбрав, например, первое выражение и записав
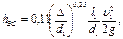
после числового решения получим рВи = 111,5 кПа.
4. Найдем избыточное давление, создаваемое насосом. Уравнение
Бернулли для участка между сечениями А и В имеет вид:

откуда, выразив 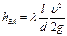 и проведя соответствующие вычисления, получим: рАи = 342 кПа.
и проведя соответствующие вычисления, получим: рАи = 342 кПа.
Задачу такого типа можно решить и графоаналитическим способом. Для этого, как обычно, сначала строятся характеристики отдельных ветвей. Но, учитывая, что нивелирные отметки и конечные давления в разных ветвях могут быть различными, начальные точки характеристик (при Q = 0) откладываются на оси на высоте h от начала координат, соответствующей сумме zi + pi/(ρg). Здесь zi - превышение конечной точки ответвления над начальной; pi избыточное давление в конечном сечении ответвления. Сумма zi + pi/(ρg) выражает дополнительный напор, затрачиваемый на подъем жидкости и преодоление конечного давления. Для задач типа примера 2.2.9, где pC = рD = pa такое смещение равно zC и zD (рис. 2.2.33).
Для трубопроводов с разомкнутыми разветвлениями (типа рис. 2.2.31, б) наиболее сложно решаются задачи на определение диаметров труб участков по заданным расходам в них. В этом случае сначала выбирается магистраль (наиболее длинная и загруженная линия), например, линия АВDЕ. Последовательно суммируя уравнения Бернулли для промежуточных сечений этой линии, пренебрегая скоростными напорами, имеем:
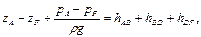
откуда среднее значение гидравлического уклона
 (2.2.23)
(2.2.23)
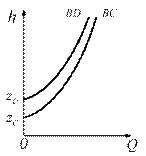
Рис. 2.2.34.
Зная icp, можно в первом приближении определить диаметр труб участка АВ из преобразованной формулы Дарси - Вейсбаха:
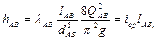 (2.2.24)
(2.2.24)
где, QAB = QC + QE + QF, dАВ легко определяется аналитически, если можно предсказать вид зависимости l = l (Re, ∆/d), т.е. формулы для определения l. Как это делается — см. раздел 2.2.2.
После определения dАВ проводят проверку правильности предположения и после его подтверждения, если это требуется, по ГОСТу определяется ближайший из имеющихся, после чего расчет повторяется для определения hAB .Зная hAB по уравнению Бернулли для сечений A и B определяют рB. Диаметры остальных ветвей последовательно определяют аналогичным способом. Если последующий проверочный расчет всего трубопровода по полученным диаметрам дает допустимое расхождение в значениях QC, QE и QF, то задача становится решенной. Если расхождения велики, то расчеты корректируются последующими приближениями.
Пример 2.2.10. Минеральное масло (ρ = 840 кг/м3, ν = 10-4 м/с) По горизонтальному трубопроводу (см. рис. 2.2.31, б) подается к раздаточным пунктам С, Е и F. Расходы масла в этих пунктах: QC = 10,6 дм3/с, QE = 6,8 дм3/с, QF = 14 дм3/с; концевые свободные напоры: НC = 67 м. HE = 0, HF = 7 м; длины участков трубопровода
lAB = 3 м, lBC = 1 км, lBD = 2 км, lDE = 1,5 км, lDF = 1,5 км. Насос при заданных расходах в пунктах раздачи может создать напор НA = 100 м, в наличии имеются новые сварные трубы диаметрами 80, 100, 125, 200, 250 мм. Подобрать диаметры всех участков трубопровода, считая потери напора в местных сопротивлениях пренебрежимо малыми. Допустимое расхождение между реальным напором НA и расчетным — не более 5 %.
Решение
1. Выберем магистральную линию АBDF и найдем для нее среднее значение гидравлического уклона icp.
Уравнение Бернулли (без учета скоростных напоров) для этой линии имеет вид:
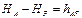 , или
, или 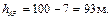
Тогда
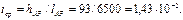
2.Определим в первом приближении и диаметр линии АВ и потери напора в ней.
Расход в этой линии
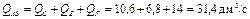 .
.
Предполагая режим движения ламинарным (высокая вязкость жидкости), используем формулу Пуазейля:
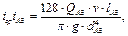
откуда
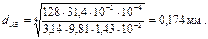
При этом
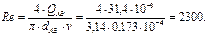
Предположение о ламинарном режиме движения нельзя считать подтвержденным, так как Re = Reкр . Кроме этого, на участке АВ расход наибольший, а, следовательно, можно ожидать, что гидравлический уклон окажется больше среднего. Поэтому, для снижения значений Re и I, выбираем ближайший к найденному больший диаметр dAB = 200 мм.
Тогда
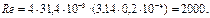
При таком диаметре режим движения действительно ламинарный. Определим потери напора на участке АВ
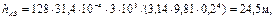
а напор в точке B
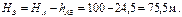
3. Определим диаметр участка ВС. Предполагая по-прежнему, что режим движения ламинарным и зная, что hBC = НB–НC = 15,5 – 67,7 = 8,5 м, получим:
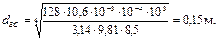
При этом 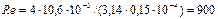 , т.е. предположение о ламинарном движении оправдалось.
, т.е. предположение о ламинарном движении оправдалось.
Найденное значение диаметра соответствует имеющимся, поэтому уточнений не требуется.
4. Определим диаметр линии ВD. Аналогично п. 2 имеем:
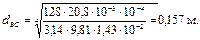
Приняв dBD = 150 мм, проверим движения:
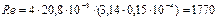 ,
,
т.е. решение правильное.

5. определим диаметр линии DE:
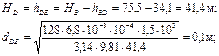
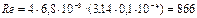 , т.е. решение правильное.
, т.е. решение правильное.
6. Определим диаметр линии DF:
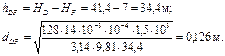
Применим диаметр равным 125 мм
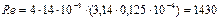 , т.е. решение правильное.
, т.е. решение правильное.
7. Проверим соответствие напора HA потерям напора в магистрали Hмаг
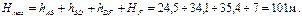
Расхождение между HA и Hмаг в 1%, решение задачи правильное.
Дата добавления: 2016-02-27; просмотров: 5146;
