ПРИБОР СКРОМНЫХ ПРОФЕССИЙ 1 страница

Мы назвали полупроводниковый диод прибором скромных профессий – именно таким он представляется начинающим и не только начинающим радиолюбителям. Это представление, по‑видимому, связано с тем, что чаще всего диод работает в схемах выпрямителей. Благодаря своей односторонней проводимости диод позволяет превратить переменный ток в постоянный, а этот постоянный ток идет на всякие вспомогательные нужды: для питания радиоламп и транзисторов, для зарядки аккумуляторов, для создания постоянных магнитных полей и т. п.

Иногда, правда, диоду доверяют и более тонкую работу – детектирование радиосигналов. Но и здесь диод делает то же, что и в выпрямителе: пропускает ток только в одну сторону. Детектор – это тоже весьма скромная, не требующая особого образования профессия полупроводникового диода.

Однако если взглянуть на дело глубже, окажется, что диод всегда выполняет операцию исключительной важности: он меняет форму электрических сигналов, преобразует их спектр. Окажется, что диод является главным представителем нескольких важнейших для всей радиоэлектроники профессий, представителем огромной самостоятельной области – нелинейной радиоэлектроники.

Научившись описывать сигнал с помощью графика (рис. 3), мы сделали лишь полдела. Важно еще суметь точно (именно точно!) описать, чем один сигнал отличается от другого, в чем похожи, а в чем непохожи их графики. Один из способов такого точного описания был предложен больше ста лет назад, когда никакой радиоэлектроники не было и в помине. Французский математик Жан‑Батист‑Жозеф Фурье решил задачу в общем, так сказать, в абстрактном виде, и лишь через много лет предложенный им способ нашел применение во многих областях техники. В том числе и в радиоэлектронике.

Представьте себе, что вам нужно с помощью карты измерить площадь какого‑либо водоема, например Черного моря. В этом случае можно поступить так: разбить всю поверхность моря на квадраты, подсчитать площадь каждого из них, а затем все полученные результаты сложить. При этом на карте разместятся два‑три больших квадрата, несколько квадратов поменьше и, наконец, множество мелких и мельчайших квадратиков, которые точно воспроизведут сложные очертания морских берегов (рис. 24).

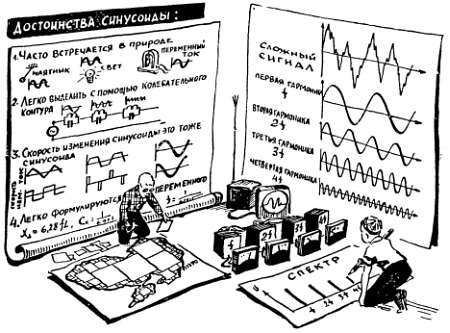
Рис. 24. Сигнал сложной формы можно представить как сумму синусоидальных составляющих с разными частотами; набор составляющих, эквивалентный сложному сигналу, называется его спектром.

Подобным же образом для точного описания сложного сигнала можно представить его как сумму стандартных составляющих– сигналов с разными частотами и амплитудами, но обязательно с одинаковыми по форме графиками. Научившись разбивать сложный сигнал на простые стандартные составляющие (подобно тому как на карте мы разбили Черное море на составляющие стандартной формы – квадраты), можно будет довольно просто составить точное описание этого сигнала. Нужно будет лишь назвать набор стандартных составляющих, которые в сумме дадут этот сложный сигнал. В качестве стандартной составляющей для измерения поверхности моря мы выбрали квадрат, хотя могли выбрать прямоугольник, ромб, круг и множество других широко известных и хорошо изученных фигур. Квадрат мы выбрали в основном потому, что измерить его площадь проще, чем площадь других фигур. Что касается стандартных составляющих, из которых лучше всего можно было бы составить сложный электрический сигнал, то выбирать эти составляющие нам не придется. Их уже давно выбрала и узаконила наука. Более того, эти составляющие выбраны самой природой. И эта честь оказана простейшим сигналам с синусоидальной формой графика.

Для того чтобы детально пояснить, почему именно синусоида была выбрана в качестве стандартной составляющей, нужно было бы написать отдельную и притом довольно большую книгу. Мы ограничимся лишь тем, что выскажем по этому поводу несколько «за».

Во‑первых, синусоидальные колебания – это одна из простейших и наиболее естественных форм движения, подобно тому как квадрат или круг – простейшая геометрическая фигура. Графики многих природных процессов – световых и звуковых колебаний, колебаний маятника, движения волн и многих других – представляют собой синусоиды. Во‑вторых, синусоида – это единственный график, скорость изменения которого представляет собой опять‑таки синусоиду. Это значит, что если мы возьмем синусоидальный сигнал и посмотрим, как изменяется скорость его нарастания или убывания, а затем построим график изменения этой скорости, то опять получим синусоиду. Это очень важное качество, так как многие процессы в электрических цепях зависят не от самой величины тока или напряжения, а именно от скорости их изменения.

В качестве примера такой зависимости рассмотрим, разумеется упрощенно, как возникает ток в цепи слюдяного конденсатора под действием переменного напряжения.

Как известно, свободные заряды через диэлектрик, в данном случае через слюду, конденсатора пройти не могут. Но под действием приложенного напряжения несколько сдвигаются, деформируются электронные орбиты атомов слюды. Происходит некоторое небольшое движение электронов (оно называется током смещения), но без их выхода из атомов. В результате деформации орбит с одной стороны диэлектрика (именно с той стороны, куда сместились орбиты) появляется отрицательный заряд, а с другой стороны появляется положительный заряд. Эти заряды притягивают или отталкивают свободные электроны в проводниках, подключенных к конденсатору, и в этих проводниках возникает ток проводимости. Однако все эти события – смещение орбит и движение электронов в проводниках – происходят лишь в тот момент, когда меняется напряжение, подведенное к конденсатору.

Если к конденсатору приложено постоянное напряжение, пусть даже очень большое, то смещенные некогда орбиты находятся в состоянии покоя и никакого движения зарядов, никакого тока в конденсаторе и во внешней цепи нет. Но стоит только напряжению измениться, как заряды совершат некоторый дополнительный сдвиг: при увеличении напряжения – в одну сторону, при уменьшении – в другую. Отсюда вывод: ток в цепи конденсатора протекает только в момент изменения напряжения. И еще один вывод: чем быстрее меняется напряжение, тем быстрее смещаются заряды, тем больше ток в цепи. Вот почему график тока через конденсатор по сути дела представляет собой график скорости изменения напряжения, приложенного к этому конденсатору. Графики эти всегда различны по форме (рис. 25), за исключением только одного случая – синусоидального напряжения. Только синусоидальное напряжение создает в цепи конденсатора ток такой же формы – синусоидальный переменный ток. Это замечательное и уникальное свойство синусоидального сигнала проявляется не только в конденсаторах, но еще и в катушках и трансформаторах, во всех так называемых реактивных элементах электрических цепей.

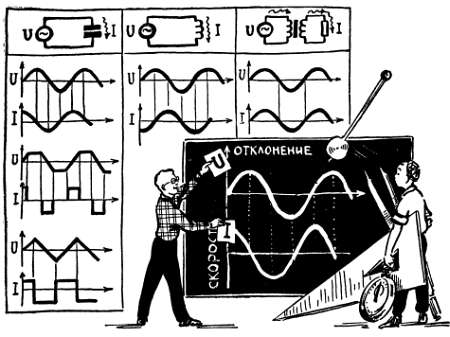
Рис. 25. Ток в цепи конденсатора протекает только при изменении напряжения на нем, и поэтому графики напряжения и тока (кроме синусоиды) различны.

Наконец, третье «за». Выбрав квадрат в качестве стандартной составляющей при разметке поверхности моря на карте, мы можем довольно просто расчертить эту поверхность, а если нужно, даже разрезать ее на составляющие. Вырезать квадрат из бумаги не составляет никакого труда. Подобно этому любой сложный сигнал можно довольно просто разделить на синусоидальные (именно на синусоидальные!) составляющие. Делается это с помощью резонансных электрических фильтров, в частности с помощью колебательных контуров. Такой контур состоит из соединенных друг с другом конденсатора и катушки (Воспоминания № 18 и № 20).

Если ввести в контур порцию электрической энергии, зарядив конденсатор или создав магнитное поле в катушке, то в контуре начнутся свободные колебания, появится переменный ток. Этот процесс очень напоминает колебания гитарной струны, которой вы также передаете порцию энергии, тронув эту струну пальцами. И, подобно тому как частота колебаний струны зависит от ее массы и силы натяжения (чем тоньше струна и чем сильнее она натянута, тем выше частота колебаний), подобно этому частота электрических колебаний в контуре зависит от емкости С конденсатора и индуктивности L катушки. Чем меньше емкость С и индуктивность L , тем выше частота колебаний.

Переменный ток, который возникает в колебательном контуре, по форме очень близок к синусоиде (в идеальном контуре, без потерь энергии, график тока – это настоящая, идеальная синусоида). Определенным образом включив колебательный контур в цепь со сложным сигналом, мы увидим, что контур выделит из этого сигнала синусоидальную составляющую своей собственной частоты (если, конечно, такая составляющая есть в сигнале). Пропустив сложный сигнал через достаточное количество настроенных контуров, можно выделить из этого сложного сигнала все его синусоидальные составляющие.

Можно не сомневаться, что после трех высказанных «за» простейшие синусоидальные сигналы будут без возражений утверждены в должности стандартных составляющих сложного сигнала. Синусоидальные колебания часто называют гармоническими, а синусоидальные составляющие сложного сигнала – гармониками. Любой сложный сигнал принято официально характеризовать его спектром – набором гармоник с указанием их амплитуды. А результат прохождения сигнала по какой‑либо цепи можно оценивать по тому, как изменился его спектр, какие новые гармоники появились в этом сигнале, какие усилились, какие ослабились. Именно с этих позиций мы и рассмотрим сейчас работу полупроводникового диода.

Включим диод в схему простейшего выпрямителя (рис. 26) и подведем к нему синусоидальное переменное напряжение.

Рис. 26. Под действием переменного напряжения в цепи диода протекает пульсирующий ток, который состоит из постоянной и переменной составляющих.

Для простоты будем считать, что диод имеет идеальную характеристику, что его обратный ток равен нулю, то есть обратное сопротивление бесконечно велико. Обычно разница между прямым и обратным током диода настолько велика, что подобное допущение вполне справедливо.

Под действием переменного напряжения в цепи диода пойдет пульсирующий ток – импульсы тока будут появляться только тогда, когда переменное напряжение приложено к диоду в прямом направлении. Иными словами, ток будет протекать лишь в течение одной половины периода переменного напряжения. Отсюда и название схемы – однополупериодный выпрямитель.

Спектр получившегося пульсирующего тока содержит гармоники с частотами, кратными частоте повторения импульсов f₁ . Первая гармоника имеет частоту f₁ , вторая в два раза более высокую частоту f₂ = 2f₁ третья частоту f₃ = 3f₁ и так далее. Амплитуды гармоник постепенно убывают – вторая оказывается слабее первой, третья слабее второй, и т. д. С помощью резонансных фильтров все эти гармоники можно выделить из пульсирующего тока, точно так же, как, пустив весь набор гармоник в общую цепь, в итоге можно получить сигнал сложной формы.

Кроме гармоник, в получившемся пульсирующем токе I_вып есть еще одна составляющая – постоянный ток I₌ . Появление этой постоянной составляющей связано с тем, что, хотя ток в цепи диода все время меняется, заряды толчками, импульсами двигаются всегда в одну сторону. Это постоянное смещение зарядов как раз и отображается постоянной составляющей I₌ . В то же время изменение тока, его пульсации отображаются всем набором гармоник.

Полупроводниковый диод в нашей схеме проводит огромную работу – он из простейшего синусоидального сигнала создает очень сложный сигнал с богатым спектром, с большим числом гармоник. В некоторых схемах такое преобразование спектра сигнала используется довольно широко. Однако в выпрямителях все получившиеся гармоники – это отходы. Здесь из всей продукции полупроводникового диода нужна только постоянная составляющая I₌ .

В однополупериодной схеме постоянная составляющая I₌ сравнительно невелика – не более 35 % амплитуды импульса тока I_макс (рис. 27–1 ).

рис. 27 –1

В то же время есть схемы, в которых I₌ оказывается вдвое больше – почти 70 % амплитуды импульса. В этих схемах для получения выпрямленного тока используются оба полупериода переменного напряжения, и называются такие схемы двухполупериодными. Никаких принципиальных отличий между одно‑ и двухполупериодными схемами нет. Можно сказать, что двухполупериодная схема – это своего рода остроумный фокус, гениальная шутка давно забытого конструктора.

Одна из двухполупериодных схем – она так и называется двухполупериодной – фактически представляет собой два однополупериодных выпрямителя, включенных так, что они работают поочередно и пропускают свои выпрямленные токи через общую нагрузку в одном и том же направлении (рис. 27–2 ). У каждого выпрямителя, у каждой половинки такой схемы свой собственный источник переменного напряжения, своя вторичная обмотка трансформатора – II' и II" . Практически для удобства намотки это одна вторичная обмотка, дающая удвоенное напряжение, от середины которой сделан отвод.

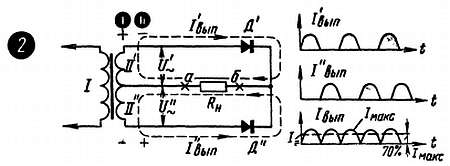
рис. 27 –2

В другом двухполупериодном выпрямителе – его схема (рис. 27–3 ) называется мостовой или мостиковой – только один источник переменного напряжения, но благодаря двум дополнительным диодам и здесь удается использовать оба полупериода для создания тока I₌ . В обеих этих двухполупериодных схемах постоянная составляющая выпрямленного тока достигает почти 70 % от I_макс .

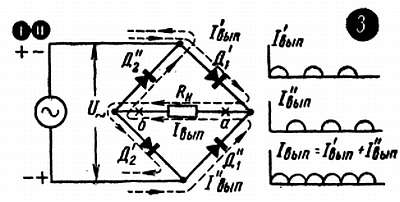
рис. 27 –3

Нагрузкой всех наших выпрямителей, как видно из схем, является некое условное сопротивление R_н . Практически же нагрузкой могут быть анодные или накальные цепи радиоламп, электродвигатель, транзисторный усилитель, обмотка электромагнита, заряжаемый аккумулятор, измерительный прибор и другие потребители.

До сих пор вместе с постоянной составляющей, которая нужна нагрузке, мы пропускали через нее и все переменные составляющие импульсного тока, все его гармоники. В некоторых случаях гармоники не вредят делу, но чаще их нельзя пускать в нагрузку – от выпрямителя, как правило, требуется «чистый» постоянный ток. Отделение переменных составляющих от постоянной осуществляется с помощью электрических фильтров.

Полностью избавиться от переменных составляющих выпрямленного тока практически нельзя, да это и не нужно. Нужно лишь ослабить их в определенное число раз, с тем чтобы эти переменные составляющие стали значительно слабее постоянной. А чтобы ослабить переменный ток, идущий в нагрузку, нужно создать для него более легкий обходный путь. Причем этот обходный путь должен быть легким только для переменных составляющих, иначе вместе с ними мы ослабим и постоянную составляющую I₌ .

Простейшим фильтром выпрямителя может служить конденсатор С_ф , подключенный параллельно нагрузке R_н (рис. 27–4 ). Постоянную составляющую этот конденсатор (как и всякий другой!) не пропускает, а для переменной он ведет себя как резистор, сопротивление которого х_с зависит от частоты f и емкости С_ф (Воспоминание № 13).

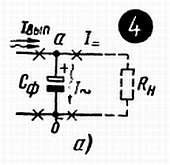
рис. 27 –4

Емкость конденсатора С_ф выбирают с таким расчетом, чтобы его сопротивление х_с было значительно меньше, чем R_н для первой гармоники выпрямленного тока, то есть для его самой низкочастотной синусоидальной составляющей. При этом исходят из того, что если конденсатор достаточно хорошо отводит от нагрузки, достаточно легко пропускает через себя первую гармонику, то он еще легче пропустит высшие гармоники, имеющие более высокие частоты, потому что емкостное сопротивление конденсатора уменьшается с частотой.

В тех случаях, когда нужна более тщательная фильтрация, более тонкая очистка выпрямленного тока от переменных составляющих, можно применить более сложные фильтры.

В П‑образном фильтре с резистором (рис. 27–5 ) уже знакомый нам конденсатор (здесь он называется С_ф2 ) выполняет свои обычные обязанности – накоротко замыкает переменные составляющие, отводит их от нагрузки. Но в этой схеме задача нашего конденсатора облегчается, так как еще до него фильтрацию осуществляет звено С_ф1R_ф . Емкостное сопротивление конденсатора С_ф1 значительно меньше, чем R_ф , и переменные составляющие в значительной степени замыкаются уже через этот конденсатор.

рис. 27 –5

Недостаток фильтра в том, что и постоянная составляющая, прежде чем она доберется до нагрузки, должна преодолеть сопротивление R_ф . На сопротивлении R_ф теряется часть энергии постоянного тока, и из‑за этого, как мы сейчас увидим; несколько снижается постоянное напряжение на нагрузке.

От такого недостатка свободен другой П‑образный фильтр (рис. 27–7 ), в котором вместо R_ф включен дроссель Др .

рис. 27 –7

Индуктивное сопротивление x_L , в отличие от емкостного x_с , уменьшается не с ростом, а с уменьшением частоты (Воспоминание № 15), а для постоянного тока индуктивное сопротивление вообще равно нулю. Поэтому постоянная составляющая I₌ встречает лишь активное сопротивление проводов дросселя, а оно невелико. В то же время переменным составляющим дроссель оказывает большое сопротивление. Такой фильтр хотя и стоит сравнительно дорого (во всяком случае, дроссель Др более сложная и дорогая деталь, чем резистор R_ф ), зато почти не снижает выпрямленного напряжения.

И, наконец, еще одна схема фильтра, применяемая сравнительно часто (рис. 27–6 ).

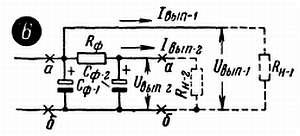
рис. 27 –6

На выходе этого фильтра мы получаем два постоянных напряжения – U_вып‑1 и U_вып‑2 . Первое из них отфильтровано хуже, второе – лучше. Но зато ток I_вып‑1 не проходит через R_ф , не теряет на нем энергии, и напряжение U_вып‑1 оказывается больше, чем U_вып‑2 . Полезность такой схемы связана с тем, что в реальной аппаратуре не все узлы требуют выпрямленного напряжения, одинаково хорошо очищенного от гармоник. Так, например, при питании некоторых мощных усилителей можно допустить, чтобы мощность гармоник составляла 1–2 % общей мощности питающего тока. В то же время для микрофонных усилителей мощность гармоник в питающем напряжении не должна превышать нескольких тысячных долей процента.

Как видите, электрические фильтры вместе с диодом участвуют в преобразовании формы сигнала, в нашем случае – в преобразовании переменного тока в постоянный. Диод усложняет спектр сигнала, создает в нем новые составляющие. Фильтры, наоборот, упрощают спектр, подавляя некоторые его составляющие. Электрические фильтры – это важнейшие и, пожалуй, самые распространенные элементы радиоэлектронных устройств. Мы будем с ними встречаться на протяжении всей книги и постепенно увидим, из каких соображений в тех или иных случаях выбираются элементы фильтра.

Так, например, уже сейчас нетрудно сообразить, что необходимая емкость конденсаторов фильтра выпрямителя зависит от того, насколько нужно очистить выпрямленный ток от гармоник, а также от величины сопротивления нагрузки R_н . Чем меньше R_н , тем меньшим должно быть и шунтирующее нагрузку емкостное сопротивление конденсаторов, тем, следовательно, большей должна быть их емкость.

Емкость этих конденсаторов зависит также и от выбранной схемы – в двухполупериодных схемах частота самой опасной (самой низкочастотной) первой гармоники в два раза выше, чем в однополупериодной схеме, так как импульсы тока следуют в два раза чаще. А это значит, что емкость фильтра конденсаторов в двухполупериодном выпрямителе может быть в два раза меньше, чем в однополупериодном.

(Проще всего, конечно, при выборе С_ф1 и С_ф2 исходить из правила «чем больше емкость фильтра, тем лучше», но такой подход может привести вас к серьезным затруднениям, причем не только схемным, но и финансовым.)

Емкость первого конденсатора фильтра С_ф1 (С_ф ) (в схеме рис. 27 – 4, 5, 6, 7 ) влияет не только на фильтрацию, но и на величину выпрямленного напряжения. Можно считать, что это напряжение создается на нагрузке постоянной составляющей тока I₌ и, согласно закону Ома, численно равно U₌ =I₌ ·R_н . Прежде чем говорить о влиянии С_ф1 (С_ф ) на напряжение U₌ , несколько слов еще об одной скромной профессии диода – о его работе в качестве ограничителя.

Давайте вместе с переменным напряжением подведем к диоду постоянное, причем так, чтобы это постоянное напряжение запирало диод, действовало на него не в прямом, а в обратном направлении (рис. 27–8 ).

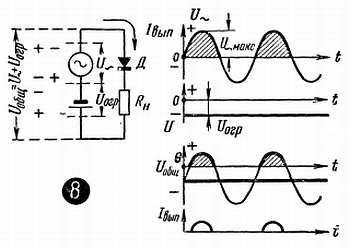
рис. 27 –8

В этом случае диод не будет пропускать ток не только во время отрицательного полупериода переменного напряжения U_~ , но в течение некоторой части положительного полупериода. Только после того, как переменное напряжение, действующее во время положительного полупериода против постоянного U_огр , полностью скомпенсирует его, только после этого диод откроется – начнет пропускать ток.

Время существования тока зависит от соотношения постоянного и переменного напряжений. Чем больше U_огр тем дольше диод остается закрытым, тем меньше времени существуют импульсы тока, или, как говорят иначе, тем сильнее они подрезаны снизу. Такое ограничение тока «снизу» обычно называют его отсечкой. Плавно изменяя U_огр , можно регулировать степень отсечки (рис. 27–10 ). Если U_огр будет больше, чем амплитуда переменного напряжения U_~макс , то диод не откроется никогда и тока в его цепи вообще не будет.

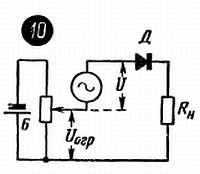
рис. 27 –10

В другой схеме диод работает ограничителем по максимуму, срезает верхушку импульса тока (рис. 27–9 ). Здесь диод Д₂ заперт, причем заперт лишь в некоторой части положительного полупериода, а в начале и в конце этого полупериода он оказывается открытым. Когда диод Д₂ открывается, то сильно шунтирует своим небольшим прямым сопротивлением нагрузку R_н2 . При этом весь ток идет через Д₂ , и импульс тока I_н2 оказывается ограниченным сверху.

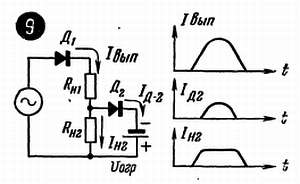
рис. 27 –9

Теперь вернемся к выпрямителям.

Для того чтобы легче было понять, что происходит в схеме, когда в ней действует переменное напряжение, можно «остановить мгновенье» и рассматривать это напряжение как постоянное, действующее то в одну, то в другую сторону. Часто можно видеть, как радиолюбители пользуются таким упрощенным методом, и рассуждения их при этом выглядят примерно так: «…Если здесь «плюс», то здесь «минус»… Если этот «минус» меньше этого «плюса», то в итоге будет «плюс»… Этот «плюс» соединен с этим «минусом», значит, оба источника действуют в одну сторону…» и т. д. Причем обозначения «плюс» и «минус» относят и к переменным напряжениям, но при этом, естественно, учитывается, что «плюс» и «минус» у них непрерывно меняются местами. Подобное отношение к переменному напряжению является, конечно, упрощением, но нам такое упрощение и нужно.

На некоторых схемах возле генератора, где действует переменное напряжение U_~ вы увидите пары «плюсов» и «минусов», а над каждой такой парой на черной точке стоит штрих или два штриха. Они‑то и показывают, какому полупериоду соответствует та или иная пара «плюс»‑«минус», та или иная полярность (временная!) переменного напряжения.

В схеме рис. 27–11 , так же как и в ограничителях (рис. 27–8, 10 ), на диод всегда действуют два напряжения – переменное с амплитудой U_~макс и постоянная составляющая выпрямленного напряжения. Причем постоянное напряжение, как и в ограничителе, действует в обратном направлении, действует против переменного, когда оно отпирает диод. И поэтому диод в выпрямителе всегда работает с отсечкой тока.

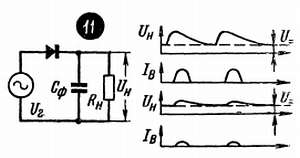
рис. 27 –11

От чего же зависит величина напряжения U₌ , которое вполне можно назвать ограничивающим напряжением? Мы уже говорили (стр. 71), что U₌ прежде всего зависит от потребляемого выпрямленного тока, а значит, от сопротивления нагрузки R_н . Но кроме того, величина U зависит еще и от емкости конденсатора С_ф1 (С_ф на схеме рис. 27–4 ).

Дело в том, что во время положительных полупериодов, то есть когда диод пропускает ток, этот конденсатор заряжается до амплитудного напряжения U_~макс , а во время отрицательных полупериодов он разряжается через нагрузку R_н (С_ф1 не может разрядиться через генератор – диод этого не допустит). Чем больше емкость конденсатора С_ф1 и чем меньше потребляемый от него ток (то есть чем больше сопротивление R_н ), тем медленнее разряжается этот конденсатор, тем меньше пульсации выпрямленного напряжения и больше его постоянная составляющая U₌ (рис. 28). Отсюда можно сделать сразу два вывода – один приятный и один неприятный.

Приятный вывод такой. Увеличивая С_ф1 можно поднять постоянное напряжение U₌ вплоть до амплитуды переменного напряжения U_~макс . Это значит, например, что если подвести к выпрямителю напряжение 6,3 в с обмотки накала ламп силового трансформатора, то можно получить U₌ около 9 в (при эффективном напряжении 6,3 в амплитуда достигает 6,3·1,4 = 8,8 в; см. стр. 148). Аналогично прямо от сети с напряжением 127 в можно получить постоянное напряжение до 180 в, а от сети 220 в – до 310 в. Не забудьте, что это максимально возможные величины. В действительности постоянное напряжение меньше, причем тем меньше, чем больше потребляемый от выпрямителя ток.

Теперь второй вывод – диод должен иметь трехкратный запас по обратному напряжению. При достаточно большой емкости С_ф1 и небольшом токе I₌ , а кроме того, во всех случаях жизни при обрыве цепи R_н напряжение U₌ примерно равно амплитуде переменного U_~макс . А это значит, что во время отрицательного (обратного) полупериода, когда диод не пропускает тока, к нему приложено два согласованно действующих и равных напряжения U₌ и U_~макс . А поскольку U_~макс ~= 1,4U_~ , то общее обратное напряжение на диоде достигает 2,8U_~ (для круглого счета примем 3U_~ ). Отсюда и сам вывод – подбирать диод для выпрямителя нужно с таким расчетом, чтобы допустимое обратное напряжение диода U_{обр‑доп} было в три раза больше, чем эффективное переменное напряжение U_~ подводимое к выпрямителю.

Для мостовых схем, где в каждое плечо последовательно включено два диода, запас напряжения для каждого из них нужен лишь полуторный. Попутно заметим, что если запаса электрической прочности у диода не хватает, если допустимое обратное напряжение у него слишком мало, то во всех схемах можно включать несколько одинаковых диодов последовательно вместо одного. При этом диоды нужно зашунтировать одинаковыми сопротивлениями по 30–100 ком (рис. 27–14 ), чтобы уравнять обратные сопротивления диодов и чтобы обратное напряжение распределялось между ними поровну. При последовательном соединении U_{обр‑доп} всех диодов суммируется.