Структура и свойства искусственного нейрона
Нейрон – это составная часть нейронной сети. На рис. 1.2 показана его структура.
.
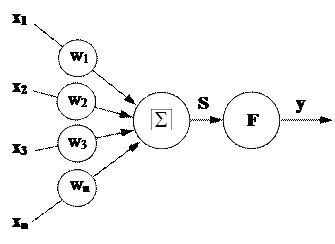
Рис. 1.2. Структура искусственного нейрона
В состав нейрона входят умножители (синапсы), сумматор и нелинейный преобразователь. Синапсы осуществляют связь между нейронами и умножают входной сигнал на число, характеризующее силу связи, - вес синапса. Сумматор выполняет сложение сигналов, поступающих по синаптическим связям от других нейронов, и внешних входных сигналов. Нелинейный преобразователь реализует нелинейную функцию одного аргумента - выхода сумматора. Эта функция называется "функция активации" или "передаточная функция" нейрона. Нейрон в целом реализует скалярную функцию векторного аргумента.
Математическая модель нейрона описывается соотношениями:
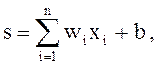
y = f(s),
где wi – вес синапса , (i = 1…n); b – значение смещения; s – результат суммирования; xi – компонента входного вектора (входной сигнал), (i = 1…n); y – выходной сигнал нейрона; n – число входов нейрона; f – нелинейное преобразование (функция активации или передаточная функция).
В общем случае, входной сигнал, весовые коэффициенты и значения смещения могут принимать действительные значения. Выход (y) определяется видом функции активации и может быть как действительным, так и целым. Во многих практических задачах входы, веса и смещения могут принимать лишь некоторые фиксированные значения.
Синаптические связи с положительными весами называют возбуждающими, с отрицательными весами – тормозящими.
Таким образом, нейрон полностью описывается своими весами wi и передаточной функцией f(s). Получив набор чисел (вектор) xi в качестве входов, нейрон выдает некоторое число y на выходе.
Описанный вычислительный элемент можно считать упрощенной математической моделью биологических нейронов – клеток, из которых состоит нервная система человека и животных.
Чтобы подчеркнуть различие нейронов биологических и математических, вторые иногда называют нейроноподобными элементами или формальными нейронами.
На входной сигнал (s) нелинейный преобразователь отвечает выходным сигналом f(s), который представляет из себя выход нейрона y.
Примеры активационных функций представлены в табл. 1.1 и на рис. 1.3.
Таблица 1.1
Виды функций активации нейронов
| Название | Формула | Область значений |
| Пороговая | 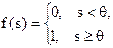
| 0, 1 |
| Знаковая (сигнатурная) | 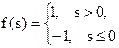
| -1, 1 
|
| Сигмоидальная (логистическая) | 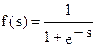
| (0, 1) |
| Полулинейная | 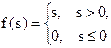
| 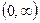
|
| Линейная | f(s) = s | 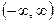
|
| Радиальная базисная (гауссова) | 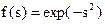
| (0, 1) |
| Полулинейная с насыщением | 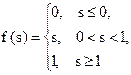
| (0, 1) |
| Линейная с насыщением | 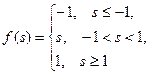
|
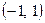
|
| Гиперболический тангенс (сигмоидальная) | 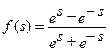
|
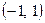
|
| Треугольная | 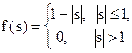
| (0, 1) |
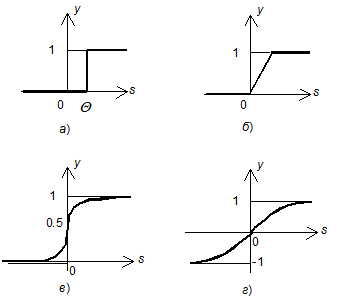
Рис. 1.3. Примеры активационных функций: а) функция единичного скачка;
б) линейный порог (гистерезис); в) сигмоид – гиперболический тангенс;
г) сигмоид – логистическая
Одной из наиболее распространенных является нелинейная функция с насыщением, так называемая логистическая функция или сигмоид (т.е. функция S-образного вида):
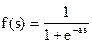 .
.
При уменьшении a сигмоид становится более пологим, в пределе при a=0 вырождаясь в горизонтальную линию на уровне 0.5, при увеличении a сигмоид приближается по внешнему виду к функции единичного скачка с порогом 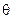 в точке s=0. Из выражения для сигмоида очевидно, что выходное значение нейрона лежит в диапазоне [0,1]. Одно из ценных свойств сигмоидной функции – простое выражение для ее производной, применение которого будет рассмотрено в дальнейшем:
в точке s=0. Из выражения для сигмоида очевидно, что выходное значение нейрона лежит в диапазоне [0,1]. Одно из ценных свойств сигмоидной функции – простое выражение для ее производной, применение которого будет рассмотрено в дальнейшем:
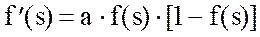 .
.
Следует отметить, что сигмоидная функция дифференцируема на всей оси абсцисс, что используется в некоторых алгоритмах обучения. Кроме того она обладает свойством усиливать слабые сигналы лучше, чем большие, и предотвращает насыщение от больших сигналов, так как они соответствуют областям аргументов, где сигмоид имеет пологий наклон. Поэтому, в силу монотонности и всюду дифференцируемости сигмоидная функция является наиболее распространённой.
Возвращаясь к общим чертам, присущим всем НС, отметим принцип параллельной обработки сигналов, который достигается путем объединения большого числа нейронов в так называемые слои и соединения определенным образом нейронов различных слоев, а также, в некоторых конфигурациях, и нейронов одного слоя между собой, причем обработка взаимодействия всех нейронов ведется послойно.
Радиально-базисная функция активации (radbas(S)) характеризуется функцией Гаусса для нормального закона распределения, в соответствии с которой:
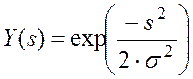 ,
,
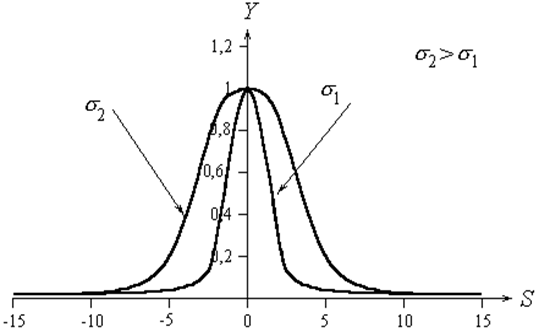
где s – cреднеквадратичное отклонение, характеризующее крутизну радиально-базисной функции (рис.1.4). Величина s определяется в соответствии с евклидовым расстоянием между входным и весовым векторами:
S2 =|X-W|2 = 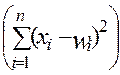 .
.
 |
Наряду с перечисленными функциями могут использоваться и другие функции активации, например, логарифмическая функция.
Рис. 1.4. Радиально-базисная функция
Многомерные радиальные распределения позволяют производить многомерный анализ путем сведения его к анализу одномерных симметричных распределений, таких как многомерное нормальное распределение или равномерное в шаре с центром в начале координат.
Дата добавления: 2016-02-24; просмотров: 2804;
