Точечные объекты высокого уровня
Два основных типа точечных объектов высокого уровня это центроиды и узлы.Центроид (centroid) обычно определяется как точка, находящаяся в точном географическом центре области или полигона (Рисунок 7.2а). Ее нахождение просто для простых многоугольников, таких как прямоугольники; когда многоугольники становятся более сложными, объем необходимых вычислений также растет. Растровые ГИС не очень хорошо приспособлены к этой процедуре. Во многих случаях даже векторные ГИС не имеют соответствующей функции. Простые, или географические, центроиды в векторном случае вычисляются поправилу четырехугольников(trapezoidal rule), которое делит многоугольник на некоторое число перекрывающихся четырехугольников. Затем вычисляются центроиды, или центральные координаты, каждого четырехугольника, потом - их взвешенное среднее (Рисунок 7.3)*. Центроид может быть нужен, когда вы создаете карту поверхности по значениям, определенным в разных ее областях. Например, если вам нужно провестиизолинии (линии равных значений) или создать fishnet map населения США, но данные собраны на уровне округов, то вам понадобится разместить центроиды в каждом из примерно трехсот округов. Затем, через интерполяцию, на основе этих точек могут быть построены изолинии или поверхности. Центроид выполняет функцию точечного объекта, к которому при известных обстоятельствах можно отнести данные полигона.
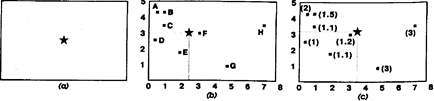
Рисунок 7.2. Простой центроид (а), центр масс (b), взвешенный центр масс (с). Числа в скобках показывают присвоенные веса, приведенные в Таблица 7.4.
Центроиды могут также помещаться в центре распределения некоторого явления, а не в абсолютном географическом центре многоугольника [Clarice, 1990]. Продолжая наш пример с картой изолиний плотности населения, мы могли бы обнаружить, что в некоторых округах большая часть населения сосредоточена ближе к одной из сторон. Хотя мы могли бы всё же использовать центроид округа для точечного представления населения, было бы более правильно поместить представительную точку ближе к центру
* Существуют и другие способы построения центроидов. Например, центроидом может считаться центр прямоугольника, описанного вокруг полигона, или центр инерции полигона. Каноническим для ГИС центроидом является центр эллипса, наиболее близкого по форме к контуру полигона. Это определение может также использоваться для сложных линий. Кроме того, оно позволяет использовать большую ось эллипса для определения ориентации полигона или сложной линии. — прим. перев.
распределения. Эта точка, называемаяцентром тяжести (center of gravity), требует раздельного усреднения координат Х и Y по всем точкам в покрытии [McGrew and Monroe, 1993; Muehrcke and Muehrcke, 1992] (Таблица 7.3, Рисунок 7.2b).
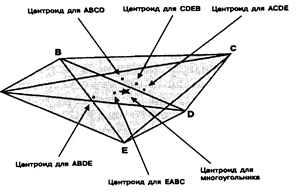
Рисунок 7.3. Правило четырехугольников. Каждый перекрывающийся четырехугольник имеет свой центроид. По этим центроидам может быть определен центроид всего многоугольника.
Таблица 7.3. расчет центра масс. Координаты центра масс группы точек определяются как частные от деления сумм координат Х и Y на число точек.
| Точка | Х | Y |
| А | 0,5 | 4.5 |
| В | • 1.0 | 4.5 |
| С | 1.0 | 3.5 |
| D | 0.5 | 2,5 |
| Е | 2.0 | 2.0 |
| F | 3.0 | 3.0 |
| G | 5.0 | 1.0 |
| Н | 7.0 | 3.5 |
| 20.0 | 24.5 | |
| Центр масс | 2.5 | 3.0625 |
Конечным результатом будет одна пара координат, представляющая центральную точку этого распределения точек. Кроме того, если эти точки имеют свои веса (например, если точки указывают и местоположения, и объемы продаж каждого магазина), то мы могли бы переместить центр распределения с учетом этого дополнительного весового фактора.
Определение такого взвешенного центра тяжести (weighted mean center) требует перемножения каждой координаты на взвешивающий коэффициент (в последнем примере - объем продаж), суммирования одноименных координат и деления сумм на общую массу [McGrew and Monroe, 1993] (Таблица 7.4, Рисунок 7.2с). В результате получаем пару координат центра распределения с учетом весовых коэффициентов.
Таблица 7.4. Расчет взвешенного центра тяжести с учетом весов, присвоенных каждой точке.
| Точка | Х | Y | k | kX | kY |
| А | 0.5 | 4.5 | 2.0 | 1.0 | 9.0 |
| В | 1.0 | 4,5 | 1.5 | 1.5 | 6.75 |
| С | 1.0 | 3.5 | 1.1 | 1.1 | 3,85 |
| D | 0.5 | 2.5 | 1,0 | 0.5 | 2.5 |
| Е | 2.0 | 2.0 | 1.1 | 2.2 | 2.2 |
| F | 3.0 | 3.0 | 1.2 | 3.6 | 3.6 |
| G | 5.0 | 1.0 | 3.0 | 15.0 | 3.0 |
| н | 7.0 | 3.5 | 3,0 | 21.0 | 10.5 |
| Сумма | 12.9 | 45.9 | 41.4 | ||
| Центр масс | 3.56 | 3.21 |
Такие вычисления применяются в крупномасштабном анализе рынка и при поиске оптимального расположения объектов торговли или массового обслуживания. Проведя их, аналитик может выбрать области вблизи вычисленного центра потенциальной территории сбыта для размещения нового торгового центра или иного предприятия. Существуют, конечно, и другие причины поиска простых центроидов; примеры включают исследования активности животных в питании [Koeppi et aL, 1985] и анализ движения центров населенности во времени как меры крупномасштабной миграции [McGrew and Monroe, 1993]. Многие растровые ГИС не имеют такой встроенной возможности, но большинство коммерческих векторных ГИС способны находить центроиды и центры тяжести.
Второй тип точечных объектов высокого уровня, узел, был упомянут в Главе 4. В этом случае точки важны не сами по себе, а как некоторые отметки на линейных и площадных объектах. Узлы не существуют как определенные объекты в растровых ГИС. Поскольку атрибутивные узлы вводятся для указания на изменение атрибутов*, возможность их идентификации жизненно важна для многих процедур работы с атрибутами. В общем случае узлы кодируются явным образом в процессе ввода и должны легко отделяться или идентифицироваться простыми процедурами поиска в ГИС. Трудность возникает только тогда, когда узел был по ошибке закодирован не как узловая, а как обычная формообразующая точка. Это еще одна иллюстрация
* в случае, если ГИС не поддерживает динамическую сегментацию — прим. перев.
важности правильной организации данных и тщательного выполнения ввода.
Здесь нужно упомянуть еще одну ситуацию, которая будет рассматриваться в следующих главах, а именно, использование групп точек для определения областей. Например, там, где имеется большое количество точек, что бы они ни представляли, образуемая ими область явно отличается от областей, в которых точек мало. Например, в определенных частях сельскохозяйственных полей может быть обнаружено большое число сорняков, что показывает на их отличие от других. Остается только определить причину различий: нарушение равновесия, недостаток пестицидов или нечто присущее местной почве или способам её обработки.
Другие характеристики распределения точечных объектов, такие как равномерность или случайность, также могут использоваться для определения областей как специфическихсообществ (communities), или областей имеющих общие рисунки распределений (Рисунок 7.4). Такое определение областей не свойственно большинству ГИС, но обычно его все-таки возможно реализовать и в растровых и в векторных системах. К этой теме мы еще вернемся.
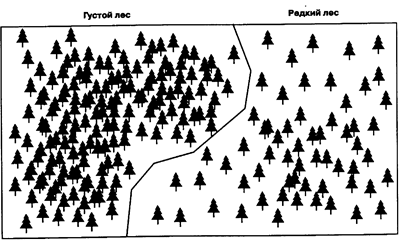
Рисунок 7.4. Сообщества, образованные на основе плотности точечных объектов.
Дата добавления: 2016-02-24; просмотров: 1947;
